Дипломная работа по методике математика. Диплом_Просветов ДВ. Изучение производной в курсе математики средней школы
 Скачать 2.34 Mb. Скачать 2.34 Mb.
|
Глава 2. Методика изучения производной в курсе средней школы2.1. Дедуктивный способСуществуют различные подходы к введению понятия производной. Нами будут рассмотрены самые распространенные и принятые в учебниках алгебры, и начала анализа. Практически все учебники, независимо от того, кто является их автором, имеют одинаковую схему введения данной темы, а именно: 1. Приводится задача, которая раскрывает физический смысл производной. 2. Формулируется понятие производной. 3. Конкретизуется понятие производной, используя ее вычисления, основой которого является определение, выяснение геометрического смысла производной, графическое отыскание производной. 4. Мотивируется необходимость изучения теорем о вычислении производных, а потом данные теоремы формулируются и доказываются. 5. Рассматриваются приложения производной. Но в процессе изучения учебников алгебры, авторами которых являются Колмогорова, Башмакова и Алимова, мы обнаружили то, что существуют и различия в изложении одного и того же материала. Таким образом, следует подробно рассмотреть эти учебники. Начнем с учебника под редакцией Колмогорова, а затем Башмакова и Алимова. В учебнике Колмогорова в ходе объяснения теории автор использует уже известные сведения о приближенном значении числа, абсолютной погрешности, точности заданного приближенного равенства, нахождении приближенного значения функции, если известна задающая ее формула. Основными также являются представления школьников о графиках известных им функций. На первом уроке учитель знакомит детей с понятием приращения функций. Также вводятся вспомогательные понятия: приращения аргумента и приращения функции, рассматривается геометрический смысл этих понятий. Далее, используя рисунок (рис. 14) вводятся определения секущей и углового коэффициента секущей проходящей через точки 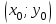 , , 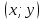 через отношение через отношение 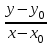 . .\ 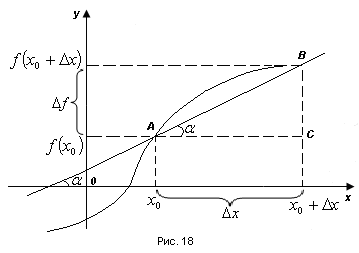 Рис. 14 Затем, используя введенные обозначения, выражается средняя скорость движения за время, а также средняя скорость изменения функции на промежутке 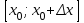 . .Далее в учебнике даются задачи, с целью – закрепить и усвоить тему первого урока. На следующем уроке дети знакомятся с понятием касательной к графику функции и понятием производной. Цель изучения данного пункта – создать наглядный образ касательной и производной в качестве углового коэффициента касательной. Эти наглядные образы способствуют восприятию определения, которые формулируются в последних пунктах. На этом же уроке рассматривают понятие мгновенной скорости. Метод нахождения производной заключается в нахождении углового коэффициента касательной или скорости изменения функции 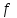 в точке в точке 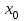 . Приведем пример алгоритма таких задач: . Приведем пример алгоритма таких задач:1. Используя формулы, которые задают функцию 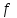 , вычисляем приращение функции в точке , вычисляем приращение функции в точке 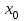 . .2. Находим выражение для разности отношения: 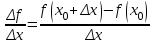 3. Выясняем к какому числу стремится отношение 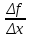 при при 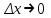 . Число которое было найдено таким способом, называется скоростью изменения функции в точке . Число которое было найдено таким способом, называется скоростью изменения функции в точке 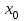 или производной функции в точке или производной функции в точке 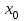 . .На следующих уроках знакомятся с понятием непрерывности и предельном переходе, правилами вычисления производных, производной сложной функции, производными тригонометрических функций и пр. Теперь рассмотрим учебники, авторами которых являются Башмакова и Алимова. У них много общего. Например, у Башмакова с помощью вводной беседы, а у Алимова с помощью подводящих задач, можно сделать вывод, что производная является скоростью. В обоих учебниках находят формулу средней скорости, используя знания физики, записывают формулу, для вычисления момента времени 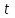 : :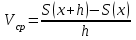 В отличие от учебника Колмогорова в учебниках Башмакова и Алимова понятие производной вводится через понятие предела: 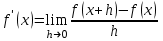 Дальше, во всех учебниках представлены примеры для того, чтобы закрепить понятие производной, а также доказывается, что 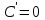 . .Также рассматривается геометрический и физический смысл производной и ее применение, и необходимо заметить, что применение производной является более трудным процессом, нежели введение данного понятия. Это связано с тем, что в школьном курсе математики не рассматривается теорема Вейерштрасса, так как на слишком громоздкая и сложная. Именно поэтому общее положение рассматривается с помощью простейших средств. Можно сформулировать теорему Вейерштрасса и проиллюстрировать для понятия на рисунках. Теорема Вейерштрасса: Непрерывная на отрезке 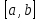 функция функция 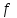 принимает на этом отрезке наибольшие и наименьшие значения. принимает на этом отрезке наибольшие и наименьшие значения.Далее выделяют такой факт, что для функции, которая является непрерывной на отрезке и отличается от постоянной, теорема Вейерштрасса гарантирует существование максимального и минимального значения, а для других функций не гарантирует. После этого решаются задачи для того, чтобы закрепить данную тему. Также детям предлагают алгоритм решения задач на max и min: 1) переменной считают величину, которую необходимо найти; вводят для нее ограничения; через нее выражаются остальные неизвестные; 2) создается функция, которая зависит от введенной переменной, той величины, о которой сказано то, что она должна быть максимальной или минимальной; 3) исследуется функция на промежутке допустимых значений переменной; 4) находятся наибольшие и наименьшие значения; 5) вычисляются другие неизвестные. |
