Дипломная работа по методике математика. Диплом_Просветов ДВ. Изучение производной в курсе математики средней школы
 Скачать 2.34 Mb. Скачать 2.34 Mb.
|
1.3. Формулы и правила дифференцирования1.3.1. Производная суммы (разности), произведения, частного функций«Находить производную, используя её определение, - занятие трудоемкое. В то же время мы знаем, что всякую элементарную функцию можно получить из некоторого набора основных функций, называемых основными элементарными функциями, используя правила сложения, умножения, деления этих функций, а также правила образования сложной функции. Значит, чтобы вычислить производную любой элементарной функции, надо знать производные основных элементарных функций и правила вычисления производных суммы, произведения, частного и сложных функций» [23]. Рассмотрим эти правила. Теорема 1. Производная суммы двух дифференцируемых функций равна сумме их производных, то есть 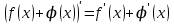 (1) (1)Доказательство: Обозначим сумму функций 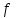 и и  через через 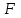 . Тогда . Тогда  , , 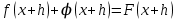 и и 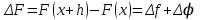 . Разделим это равенство на . Разделим это равенство на  и найдем предел полученного отношения при и найдем предел полученного отношения при  : : 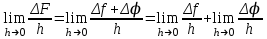 (2) (2)Так как 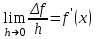 , а , а 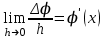 , то из равенства (2) следует, что , то из равенства (2) следует, что  , то есть , то есть 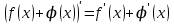 . .Теорема доказана. «Физический смысл теоремы состоит в том, что при сложении движений их скорости складываются. Например, если человек идет по движущемуся вагону в направлении движения, то его скорость относительно земли равна сумме скоростей движения вагона и скорости человека относительно вагона» [12]. Пример 1. Найдем производную функции 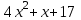 . .Решение. Так как 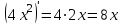 ; ; 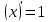 ; ; 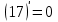 , то , то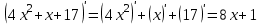 . .Теорема 2. Производная произведения двух дифференцируемых функций равна сумме двух слагаемых: производной первой функции, умноженной на вторую функцию и первой функции, умноженной на производную второй функции. Иными словами, выполняется равенство: 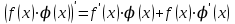 (3) (3)Доказательство. Обозначим произведение функций 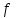 и и  через через 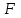 . Тогда . Тогда 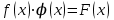 ; ; 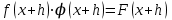 . (4) . (4)Так как‚  и и 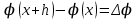 , то , то 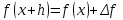 и и 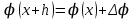 . .Значит, 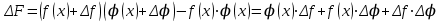 (5) (5)Разделим равенство (4) на  и найдем предел при и найдем предел при  . Тогда получим: . Тогда получим: 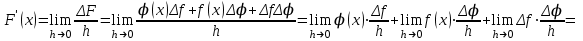  . .Так как 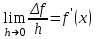 , , 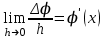 , ,  , то равенство (5) имеет вид , то равенство (5) имеет вид 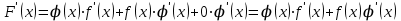 Таким образом, доказана формула 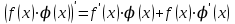 Пример 2. Найдем производную от функции 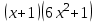 . .Решение. В данном случае 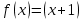 ; ; 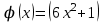 . .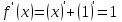 ; ; 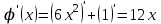 . .Поэтому 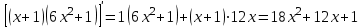 . .Следствие. Производная степенной функции 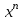 , ,  может быть вычислена по формуле может быть вычислена по формуле (6) (6)Доказательство. Воспользуемся методом математической индукции. Мы уже знаем, что 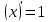 , то есть формула (6) для , то есть формула (6) для 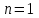 верна. Предположим, что она верна для верна. Предположим, что она верна для 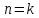 и докажем справедливость формулы для и докажем справедливость формулы для 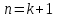 . .Используя формулу (З), находим 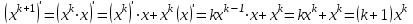 . Итак, . Итак, , то есть формула (6) верна и для , то есть формула (6) верна и для 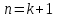 . Следовательно, по принципу математической индукции, эта формула верна для всех натуральных чисел . Следовательно, по принципу математической индукции, эта формула верна для всех натуральных чисел 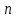 . .Пример 3. Найдем производную функции 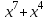 . .Решение. 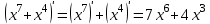 . .Примечание. В более подробных курсах доказывается, что формула (6) справедлива для степенной функции  , ,  , когда показатель степени любое действительное число. То есть имеет место формула , когда показатель степени любое действительное число. То есть имеет место формула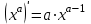 (7) (7)Выведем теперь формулу для вычисления производной дроби. Сначала докажем следующую теорему: Теорема 3. В точках, где дифференцируемая функция 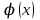 не обращается в нуль, производная функции не обращается в нуль, производная функции 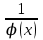 выражается формулой: выражается формулой: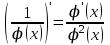 (8) (8)Доказательство. Воспользовавшись формулой (2), имеем 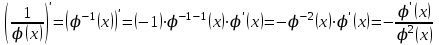 Теорема доказана. Пример 4. Найдем производную функции 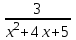 . .Решение. Здесь 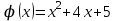 и и 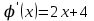 . Значит, по формуле (8), имеем . Значит, по формуле (8), имеем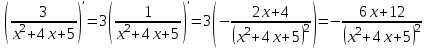 . .Теорема 4. Если функции 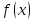 и и 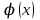 дифференцируемы, то в точках, где функция дифференцируемы, то в точках, где функция 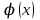 не обращается в нуль, производную дроби не обращается в нуль, производную дроби  можно найти по формуле можно найти по формуле (9) (9)Доказательство. Функцию 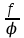 можно записать в виде можно записать в виде  . Применяя формулу для производной произведения и формулу (8), получим . Применяя формулу для производной произведения и формулу (8), получим 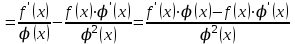 Теорема доказана. Пример 4. Найдем производную функции 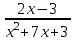 . .Решение. Здесь 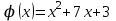 и и  , , 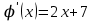 . .По формуле (9) получаем 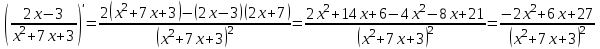 1.3.2.Производная степенной функции и дробиВ предыдущем пункте мы установили справедливость формулы  . Покажем, что похожая формула имеет место и для производной степени функции‚ . Покажем, что похожая формула имеет место и для производной степени функции‚  , где , где 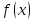 - дифференцируемая функция. Вычислим вначале производную квадрата для дифференцируемой функции - дифференцируемая функция. Вычислим вначале производную квадрата для дифференцируемой функции 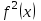 . Здесь . Здесь 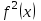 означает произведение означает произведение  , поэтому по формуле , поэтому по формуле 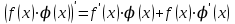 (1) (1)получаем 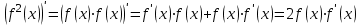 Если рассмотреть функцию 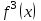 , то , то 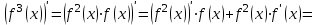 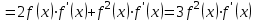 . .Аналогичную формулу получим для  и т.д. Предположим теперь, что формула и т.д. Предположим теперь, что формула 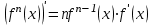 (2) (2)справедлива для 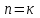 и покажем, что она имеет место и для и покажем, что она имеет место и для 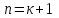 . Действительно, . Действительно, 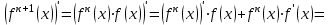  следовательно, по принципу математической индукции формула (2) верна для любого натурального числа.[23] В более подробных курсах математического анализа доказывается, что формула (2) верна для функции 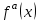 , ,  , где , где 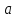 - любое действительное число, то есть - любое действительное число, то есть 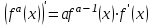 (3) (3)Пример 1. Найдем производные функций: а) 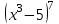 , б) , б)  , в) , в)  Решение. По формуле (2) находим а)  , ,6) 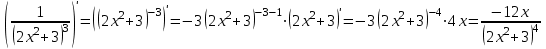 , ,в) 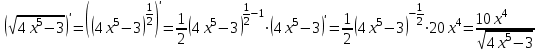 . .Пример 2. Найдем производную функции 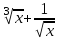 . .Решение. 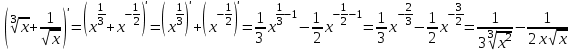 1.3.З. Производные тригонометрических функцийФормулы для производных тригонометрических функций имеют вид:  (1) (1)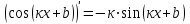 (2) (2)В частности, при 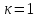 и и 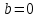 получаем получаем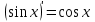 (3) (3) (4) (4)Докажем для примера формулу (1). Прежде чем приступить к доказательству, напомним, что тригонометрические функции непрерывны в каждой точке своей области определения. Это значит, например, что 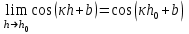 , то есть при вычислении предела этих функций при , то есть при вычислении предела этих функций при 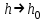 достаточно в функцию подставить значение аргумента достаточно в функцию подставить значение аргумента 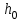 . .Напомним, что первый замечательный предел означает равенство  . Нетрудно видеть, что тогда при любом действительном значении . Нетрудно видеть, что тогда при любом действительном значении  будет справедливо и такое равенство будет справедливо и такое равенство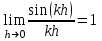 (5) (5)Действительно, если обозначить 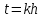 , то при , то при  имеем имеем 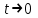 и, наоборот, при и, наоборот, при 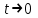 будет будет  . .Сделав подстановку 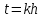 в равенстве (5), получим в равенстве (5), получим  Итак, рассмотрим функцию 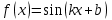 , тогда , тогда  . Найдем приращение функции, используя формулу преобразования разности синусов в произведение: . Найдем приращение функции, используя формулу преобразования разности синусов в произведение:  . Найдем . Найдемтеперь предел  отношения при отношения при  , используя правило вычисления предела произведения функций, первый замечательный предел и непрерывность тригонометрических функций: , используя правило вычисления предела произведения функций, первый замечательный предел и непрерывность тригонометрических функций: 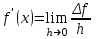 (6) (6)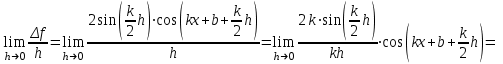  . .Здесь учтено, что  , а , а  . .Итак, из равенства (6) следует,  . .Пример 1. Найдем производные функций: а) 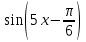 , б) , б) 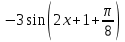 . .Решение. По формуле (1), имеем а) 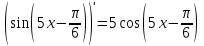 , ,б)  Чтобы доказать формулу (2), достаточно вспомнить, что по формулам приведения 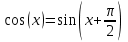 , а , а  , поэтому , поэтому . .Найдем теперь производную функции 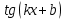 . Применяя правило вычисления производной дроби и формулы (1) и (2), получаем: . Применяя правило вычисления производной дроби и формулы (1) и (2), получаем: 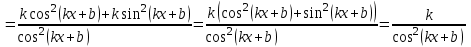 . .Итак, 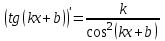 (7) (7)В частности, если положить в формуле (7) 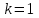 , , 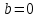 , то получим , то получим (8) (8)Совершенно аналогично получим формулы 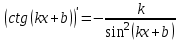 (9) (9) (10) (10)Пример 2. Найдем производные функций. а) 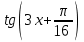 , , Решение. а) По формуле (7) имеем 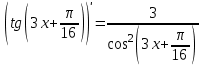 , ,1.3.4. Число е. Производные показательной и логарифмической функций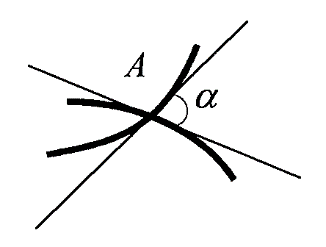 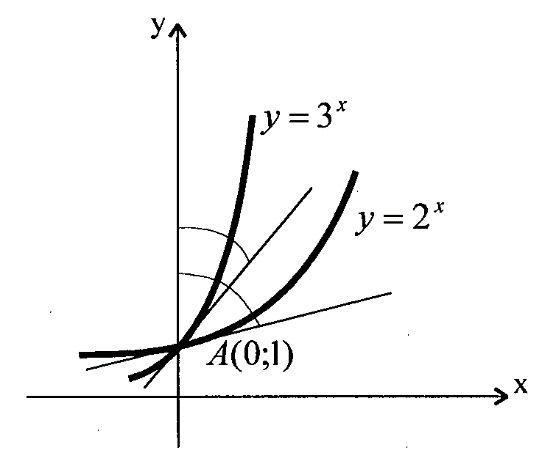 Рис. 5 Рис. 6 Угол, который образуют две кривые – это угол между касательными к данным кривым, которые проведены в точку, где они пересекаются (рис. 5). «На рисунке 4 изображены графики функций 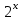 и и 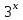 . Они пересекают ось Оу в одной точке . Они пересекают ось Оу в одной точке 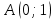 . График функции . График функции 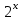 образует с осью ординат угол образует с осью ординат угол 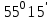 , а график функции , а график функции 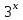 - угол - угол 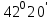 . Если увеличивать основание . Если увеличивать основание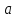 показательной функции показательной функции 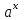 от 2 до З, то угол в этом случае будет уменьшаться от от 2 до З, то угол в этом случае будет уменьшаться от 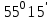 до до 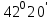 , и найдется такое значение , и найдется такое значение 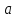 , при котором график функции , при котором график функции 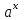 пересечет ось Оу под углом пересечет ось Оу под углом  . Это значение . Это значение 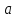 обозначают буквой обозначают буквой 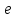 . Ясно, что касательная к графику функции . Ясно, что касательная к графику функции 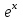 в точке в точке 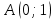 наклонена к оси Ох также под углом наклонена к оси Ох также под углом  (рис. 6). Поэтому, угловой коэффициент этой касательной равен 1, (рис. 6). Поэтому, угловой коэффициент этой касательной равен 1, 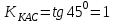 . Было установлено, что число . Было установлено, что число 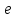 является иррациональным5, иными словами, это бесконечная десятичная непереодическая дробь: является иррациональным5, иными словами, это бесконечная десятичная непереодическая дробь: 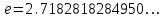 » [7] » [7]Необходимо сказать, что функцию 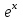 обозначают также обозначают также 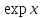 , которая читается как «экспонента , которая читается как «экспонента 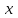 » (от латинского слова “exponere - показывать”). » (от латинского слова “exponere - показывать”).«Число 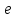 связано с формулой сложных процентов. Например, если мы одолжили определенную сумму рублей под связано с формулой сложных процентов. Например, если мы одолжили определенную сумму рублей под 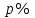 годовых, то через годовых, то через 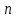 лет следует вернуть сумму лет следует вернуть сумму  , то есть, при , то есть, при  сумма долга будет составлять сумма долга будет составлять 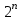 рублей» [14]. рублей» [14].«Предположим, что капитализация происходит не каждый год, а каждый месяц, но процентная ставка в 12 раз меньше. Тогда за год возвратный капитал будет составлять сумму 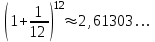 . Если капитализацию совершать каждый день (такое бывает во времена больших финансовых кризисов), но процентная ставка будет в 365 раз меньше, то через год сумма долга будет выражаться числом . Если капитализацию совершать каждый день (такое бывает во времена больших финансовых кризисов), но процентная ставка будет в 365 раз меньше, то через год сумма долга будет выражаться числом 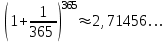 можно видеть, что значения постепенно приближаются к числу можно видеть, что значения постепенно приближаются к числу 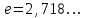 » [23]. Поэтому можно считать, что если увеличиваются » [23]. Поэтому можно считать, что если увеличиваются 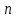 числа, то точнее выражается число числа, то точнее выражается число 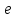 . В курсах математического анализа доказывается, что . В курсах математического анализа доказывается, что 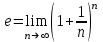 (1) (1)Логарифмы, основание которых 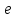 называются натуральными логарифмами. Натуральный логарифм числа называются натуральными логарифмами. Натуральный логарифм числа 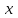 обозначают обозначают 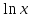 . Итак, . Итак, 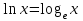 . Так как, функция . Так как, функция 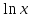 является обратной функции является обратной функции 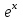 , то ее график получается из графика функции , то ее график получается из графика функции 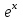 благодаря осевой симметрии относительно прямой благодаря осевой симметрии относительно прямой  (рис. 3). Нужно отметить, что (рис. 3). Нужно отметить, что 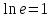 , , 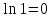 . .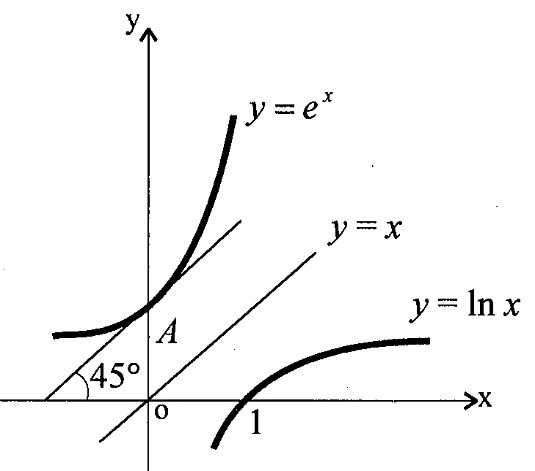 Рис. 7 Теперь необходимо вычислить производную от функции 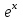 . Поэтому сначала необходимо доказать следующее утверждение: . Поэтому сначала необходимо доказать следующее утверждение: (2) (2)Учитывая определение числа 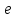 , угловой коэффициент касательной к графику функции , угловой коэффициент касательной к графику функции 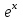 в точке в точке  равен равен 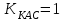 . С другой стороны, используя формулу (2), коэффициент касательной к графику функции . С другой стороны, используя формулу (2), коэффициент касательной к графику функции 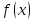 в точке в точке 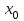 можно найти по формуле можно найти по формуле . .Для функции 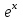 в точке в точке  , имеем , имеем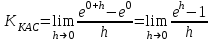 А так как в этой точке 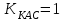 , то , то  . Заметим, что поскольку при . Заметим, что поскольку при  имеем имеем 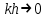 , из равенства (2) следует, что при , из равенства (2) следует, что при  (3) (3)Пусть 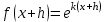 и потому и потому 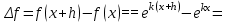 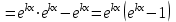 . .Найдем теперь предел отношения  при при  . .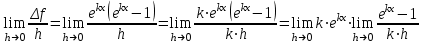 (4) (4)При изменении  величина величина 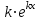 не изменяется, поэтому не изменяется, поэтому 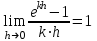 . Тогда из равенства (4), получаем . Тогда из равенства (4), получаем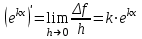 (5) (5)В частности, при 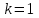 имеем имеем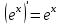 (6) (6)Таким образом, производная функции 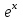 равна самой этой функции. Именно этим объясняется особая роль числа равна самой этой функции. Именно этим объясняется особая роль числа 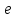 в математике. в математике.Отметим, что 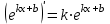 (7) (7)В самом деле, 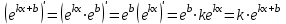 Пример 1. Найдем производные функций  ; ; Решение. Применяя формулу (7) при 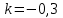 и и 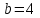 , получаем , получаем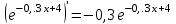 Пример 2. Найти касательную к графику функции 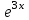 в точке с абсциссой в точке с абсциссой  . .Решение. Уравнение касательной к графику функции 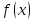 в точке с абсциссой в точке с абсциссой 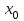 имеет вид: имеет вид: . .В данном случае  ; ; 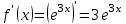 , ,  . Значит, уравнение искомой касательной имеет вид . Значит, уравнение искомой касательной имеет вид  , то есть , то есть 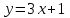 . .Рассмотрим функцию 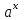 при любом при любом 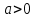 , , 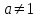 . Так как . Так как  , то , то 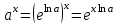 . По формуле (5) при . По формуле (5) при 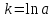 получаем получаем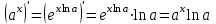 Итак, 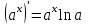 (8) (8)Можно доказать, что 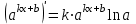 (9) (9)Пример 3. Найдем производную функции 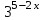 Решение. По формуле (9) при 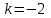 и и 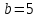 получаем получаем 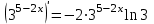 . .Приведем без вывода формулу вычисления производной логарифмической функции: 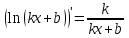 (10) (10)В частности, при 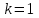 , , 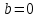 имеет место формула имеет место формула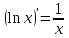 (11) (11)Логарифм с произвольным основанием 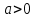 , , 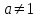 можно свести к натуральному логарифму по формуле можно свести к натуральному логарифму по формуле 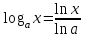 . Поэтому . Поэтому . .Итак,  (12) (12)Аналогично можно получить формулу  (13) (13)Пример 4. Найдем производную функции: а)  ; ; Решение. а) По формуле (10) при 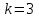 , ,  , имеем , имеем 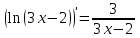 ; ; |
