Дипломная работа по методике математика. Диплом_Просветов ДВ. Изучение производной в курсе математики средней школы
 Скачать 2.34 Mb. Скачать 2.34 Mb.
|
1.6. Наибольшее и наименьшее значение функцииС помощью производной можно находить наибольшие и наименьшие значения функции  на отрезке на отрезке 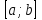 . Этих значений непрерывная функция достигает либо в критических точках, либо в концах отрезка (a и b). . Этих значений непрерывная функция достигает либо в критических точках, либо в концах отрезка (a и b).Предположим, что функция  является непрерывной на отрезке является непрерывной на отрезке 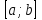 . Тогда на данном отрезке она достигает максимального значения. Пусть, на данном отрезке функция . Тогда на данном отрезке она достигает максимального значения. Пусть, на данном отрезке функция  имеет определенное количество критических точек. Если максимальное значение достигается внутри отрезка имеет определенное количество критических точек. Если максимальное значение достигается внутри отрезка 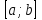 , то это значение – это один из максимумов функции, если максимумов несколько, но может быть и так, что максимальное значение будет достигаться на одном из концов отрезка. , то это значение – это один из максимумов функции, если максимумов несколько, но может быть и так, что максимальное значение будет достигаться на одном из концов отрезка.Таким образом, функция на отрезке 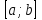 имеет максимальное значение или на одном из концов отрезка, или в такой внутренней точке данного отрезка, которая является точкой максимума. Это же касается и минимального значения функции: оно может достигаться или на одном из концов отрезка, или в такой внутренней точке данного отрезка, которая является точкой минимума. Из предыдущего вытекает правило11: если необходимо найти наибольшее значение непрерывной функции на отрезке имеет максимальное значение или на одном из концов отрезка, или в такой внутренней точке данного отрезка, которая является точкой максимума. Это же касается и минимального значения функции: оно может достигаться или на одном из концов отрезка, или в такой внутренней точке данного отрезка, которая является точкой минимума. Из предыдущего вытекает правило11: если необходимо найти наибольшее значение непрерывной функции на отрезке 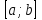 , то для этого нужно: , то для этого нужно:1) определить критические точки; 2) определить значение функции в критических точках; 3) определить значение функции на концах отрезка; 4) выбрать максимальное и минимальное значение функции. Аналогично поступаем в ходе определения минимального значения функции на отрезке. Пример. Найти наибольшее и наименьшее значения функции 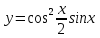 на отрезке [0, на отрезке [0,  ]. ].Решение: 1) Находим 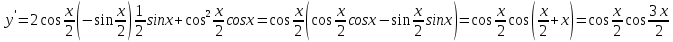 2) Находим критические точки 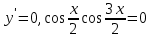 , ,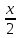 = =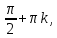 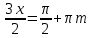 ; ;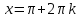 , x= , x=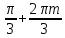 . .В отрезок [0,  ] попадают две критические точки ] попадают две критические точки 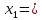 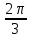 , , 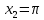 . .3) Находим значение функции в концах отрезка и в критических точках 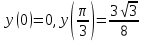 , , 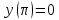 Ответ: 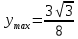 , , 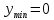 . .1.7. Исследование функции с помощью производнойПостроение графика произвольной функции может быть, как отдельной задачей, так и вспомогательной - например, при решении уравнений графическим способом, или при решении задач с параметрами. Алгоритм исследования функции  и построения ее графика таков: и построения ее графика таков:1. Находим область определения (D(f)) функции  . .2. Если область определения функции симметрична относительно нуля (то есть для любого значения x из D(f) значение x также принадлежит области определения, то проверяем функцию на четность. Если 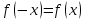 , то функция четная. (Примером четной функции является функция , то функция четная. (Примером четной функции является функция 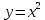 ) )Для нас важно, что график четной функции симметричен относительно оси OY. Если 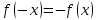 , то функция нечетная. (Примером нечетной функции является функция , то функция нечетная. (Примером нечетной функции является функция 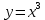 ) )График нечетной функции симметричен относительно начала координат. Если функция является четной или нечетной, то мы можем построить часть ее графика для 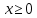 , а затем соответствующим образом отразить ее. , а затем соответствующим образом отразить ее.3. Находим точки пересечения графика с осями координат. Находим нули функции - это точки пересечения графика функции  с осью абсцисс (OX). с осью абсцисс (OX).Для этого мы решаем уравнение 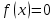 . .Корни этого уравнения являются абсциссами точек пересечения графика функции с осью ОХ. Находим точку пересечения графика функции  с осью ординат (OY). Для этого ищем значение функции при с осью ординат (OY). Для этого ищем значение функции при 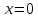 . .4. Находим промежутки знакопостоянства функции, то есть промежутки, на которых функция  сохраняет знак. Это нам потребуется для контроля правильности построения графика. сохраняет знак. Это нам потребуется для контроля правильности построения графика.Чтобы найти промежутки знакопостоянства функции  , нам нужно решить неравенства , нам нужно решить неравенства 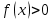 и и 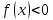 . .5. Находим асимптоты графика функции. 6. Если функция периодическая, то находим период функции. 7. Исследуем функцию с помощью производной: находим промежутки возрастания и убывания функции, а также точки максимума и минимума. Для этого мы следуем привычному алгоритму. а) Находим производную 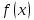 . .б) Приравниваем производную к нулю и находим корни уравнения  - это стационарные точки. - это стационарные точки.в) Находим промежутки знакопостоянства производной. Промежутки, на которых производная положительна, являются промежутками возрастания функции. Промежутки, на которых производная отрицательна, являются промежутками убывания функции. Точки, в которых производная меняет знак с плюса на минус, являются точками максимума. Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума. 8. И последнее, что необходимо найти - точки перегибы и промежутки выпуклости и вогнутости. Подробнее о том, как находить точки перегиба и промежутки выпуклости и вогнутости рассмотрим на примере. Итак, давайте, для примера, исследуем функцию 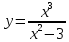 и построим ее график. и построим ее график.1. Найдем D(y).  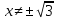 Сразу отметим, что при  знаменатель дроби равен нулю, следовательно, прямые знаменатель дроби равен нулю, следовательно, прямые 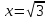 и и 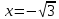 являются вертикальными асимптотами графика функции являются вертикальными асимптотами графика функции 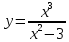 . .2. Исследуем функцию на четность. Область определения функции симметрична относительна нуля (мы выкололи две симметричные точки: 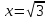 и и  ) ) Получили, что  , следовательно, функция , следовательно, функция  -нечетная, и график функции симметричен относительно начала координат. -нечетная, и график функции симметричен относительно начала координат.3. Найдем точки пересечения с осями координат. а) Точки пересечения с осью ОХ (y=0) 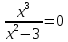 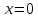 б) Точка пересечения с осью ОY (x=0) 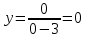 График нашей функции проходит через начало координат. 4. Найдем промежутки знакопостоянства. Решим неравенство 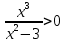 Воспользуемся методом интервалов. Найдем корни числителя и знаменателя, нанесем их на числовую ось и расставим знаки: Корень числителя: 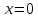 Корни знаменателя: 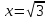 и и 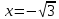 ; ;Расставим знаки:  Итак, 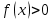 при при 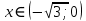 и и 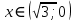 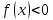 при при 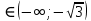 и и 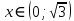 5. Найдем асимптоты графика функции 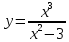 . .Вертикальные асимптоты мы уже нашли в п.1, это прямые 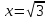 и и 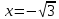 . .Уравнение горизонтальной асимптоты функции 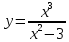 имеет вид имеет вид 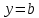 , где , где 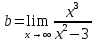 . .Степень числителя дроби 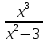 на единицу больше степени знаменателя, поэтому на единицу больше степени знаменателя, поэтому 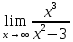 не существует, и график функции не существует, и график функции 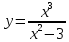 не имеет горизонтальной асимптоты. не имеет горизонтальной асимптоты.Попробуем найти наклонную асимптоту. Уравнение наклонной асимптоты имеет вид 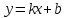 . .Коэффициенты 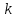 и и 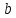 вычисляются следующим образом: вычисляются следующим образом: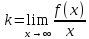 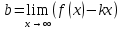 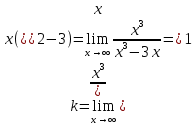 В нашем случае. 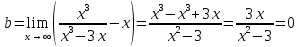 (Степень знаменателя на единицу больше степени числителя). То есть уравнение наклонной асимптоты имеет вид 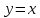 . .Нанесем асимптоты на координатную плоскость: 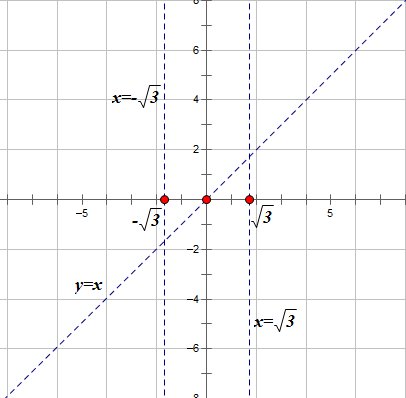 6. Найдем промежутки возрастания-убывания функции 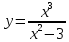 и экстремумы. и экстремумы.а) Найдем производную функции 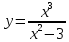 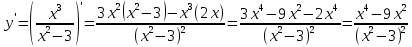 б) Приравняем производную к нулю: 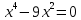 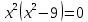 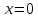 (корень четной кратности); (корень четной кратности); 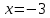 ; ; 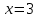 . .Корни знаменателя  - также корни четной кратности. - также корни четной кратности.В корнях четной кратности производная знак не меняет. в) Нанесем нули производной и корни ее знаменателя на числовую ось, расставим знаки и найдем точки экстремума и промежутки возрастания и убывания. 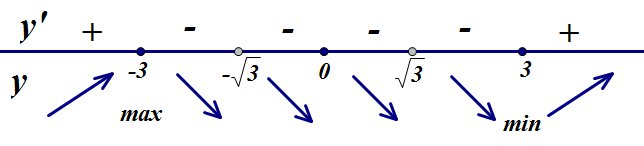 Итак, мы нашли промежутки возрастания и убывания. Найдем значение функции в точках экстремума: 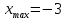 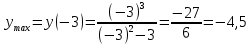 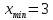 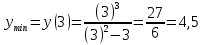 Заметим, что, поскольку функция 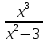 нечетная, и мы нашли, что нечетная, и мы нашли, что 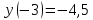 , мы могли бы сразу написать, что , мы могли бы сразу написать, что 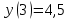 . .Итак, отметим в нашей координатной плоскости точки минимума и максимума функции и точку пересечения графика функции с осями координат. На рисунке ниже большими красными кружками обозначены точки, через которые проходит график функции. 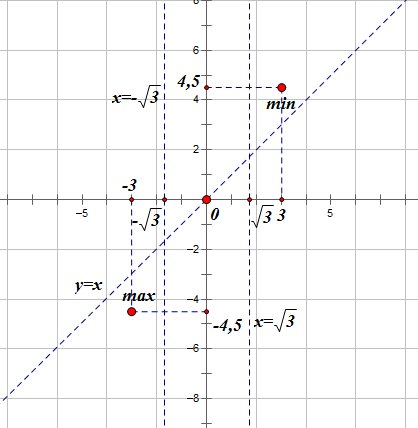 Теперь учтем промежутки возрастания-убывания и промежутки знакопостоянства функции (п. 4) и построим ее график. Помним, что график функции не пересекает абсциссы, он лишь приближается к ним.  После построения графика необходимо еще раз просмотреть все пункты исследования функции и проверить, соответствует ли полученный график всем пунктам. Если наблюдается какое-то несоответствие, то необходимо повторить исследование и найти причину нестыковки графика и поведения функции. |
