Элементарная биометрия. Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях

• Название: Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях
• Анкор: Элементарная биометрия.doc
• Дата: 04.01.2018
• Размер: 3.04 Mb.
• Имя файла: Элементарная биометрия.doc
• Тип: Книга; #13667
• страница: 15 из 32

Корреляционный анализ

Взаимная связь (взаимная зависимость) двух при­знаков при их изменчивости, т. е. сопряженность их вариации, называется корреляцией. Корреляция имеет место в тех случаях, когда признаки из­меняются не автономно, а согласованно. Если с уве­личением одного признака происходит со­ответствующее уве­личение другого, говорят о положительной корреляции, и коэффициент корреляции имеет в этом случае положительный знак (+). Если же по мере увеличения первого признака второй уменьшается, то это отрицательная корреляция, коэффициент корреляции пишется со знаком минус (−). Полная положительная корреляция выражается единицей r= 1, пол­ная отрицательная r= −1. В природе такая ситуация встречается редко, и степень связи выражается той или иной долей единицы. При этом о тесной (сильной) корреляции обычно говорят в тех случаях, когда коэффициент корреляции не ниже ±0.6; значения ниже ±0.6 указывают на среднюю связь, а ниже ±0.3 – на слабую.

Коэффициент корреляции призван численно выражать долю сопряженной вариации двух признаков в общей их вариации: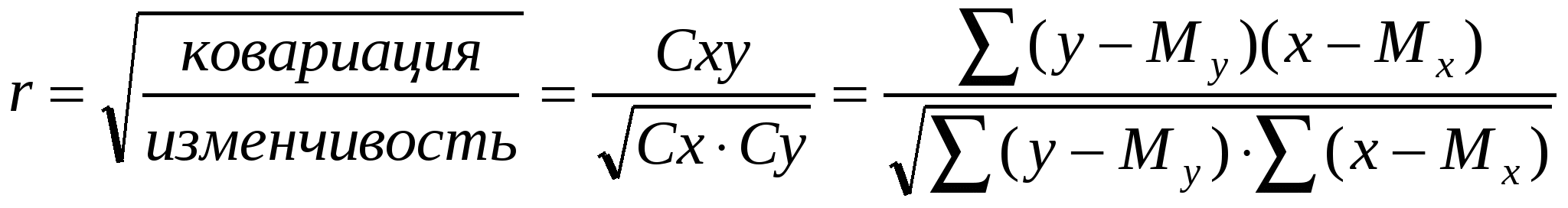

,

где Cxy – характеристика сопряженной изменчивости признаков,

Cx,Cy – характеристика общей изменчивости признаков.

При большом количестве данных коэффициент корреляции имеет смысл вычислять на компьютере (например, с помощью функции КОРРЕЛ в среде программы Excel), но для небольших выборок его можно быстро найти и при ручном счете. Рабочая формула для расчетов имеет вид:

.

Способ вычисления коэффициента корреляции показан в таблице 13 на примере зависимости меж­ду живым весом коров (х) и их приплода (у, кг). По таблице рас­считываются квадраты вариант и их произведения, а также суммы вариант, квадратов и произведений. Вычисления ведут­ся по точным рабочим формулам.

Таблица 13

i	у	х	у²	х²	х∙у
1	25	352	625	123904	8800
2	26	376	676	141376	9776
3	31	402	961	161604	12462
4	32	453	1024	205208	14496
5	34	484	1156	234256	16456
6	38	528	1444	278784	20064
7	38	555	1444	308025	21090
Σ	224	3150	7330	1453158	103144

Проведем последовательные расчеты. Сначала определим вспомогательные величины:

Cxy = Σ(x∙y)−(Σx)∙(Σy) / n = 103144 − 3150 ∙ 224 / 7 = 2344,

Cy = Σy² − (Σy)² / n = 7330 − 224² / 7 = 162,

Cx = Σx² − (Σx)² / n = 1453158 − 3150² / 7 = 35658;

затем – коэффициент корреляции:

= 0.975.

Далее найдем его ошибку:

,

и, наконец, критерий t Стьюдента для проверки значимости коэффициентов:

t_r= r / m_r = 0.975 / 0.099 = 9.84.

Нулевая гипотеза предполагает отсутствие связи: «коэффициент корреляции значимо от нуля не отличается», r= 0. В нашем примере для уровня значимости α = 0.05 и числа степеней свободы df= n− 2 = 5 находим табличное значение критерия Стьюдента t_(0.05, 5) = 2.57. Полученная величина (9.84) значительно превышает табличную (2.57), что говорит о высокой статистической значимости коэффициента корреляции, о достоверности его отличия от нуля. Признаки положительно коррелируют, масса тела теленка действительно возрастает вслед за ростом массы тела коровы.

Выборный коэффициент корреляции в той или иной степени соответствует генеральному параметру. Определить диапазон, где лежит генеральное значение, можно с помощью доверительного интервала, хотя его нельзя построить непосредственно по формуле r± t_(α, df) ∙ m_r. Дело в том, что область изменений коэффициента ограничена рамками ±1, поэтому распределение выборочных коэффициентов корреляции в общем не соответствует нормальному (с диапазоном изменчивости ±∞). Поэтому перед расчетом коэффициент корреляции преобразуют в величинуz, имеющую нормальное распределение, и уже для нее отыскивают границы доверительного интервала, после чего выполняют обратное преобразование.

Доверительный интервал для нашего случая (r= 0.975, α = 0.05, п = 7, df= п − 2 = 5, t_(0.05,5) = 2.57) рассчитывается так. Преобразуем r:

 = 2.184

или берем его более точное значение из таблицы 13П, тогдаz= 2.0923.

Определяем ошибку = 0.5.

Находим верхнюю границу: _maxz= z + t_(α,df)  ∙ m_z= 2.09+2.57∙0.5 = 3.375 и нижнюю границу: _minz= z − t_(α,df)  ∙ m_z= 2.09−2.57∙0.5 = 0.805.

Обратное преобразование (по табл. 14П) дает: _maxr≈ 1.00, _minr≈ 0.67. Истинное значение коэффициента корреляции находится в диапазоне от 0.67 до 1.00.