Элементарная биометрия. Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях
 Скачать 3.04 Mb. Скачать 3.04 Mb.
|
|
Однофакторным называется анализ, изучающий действие на результативный признак только одного организованного фактора А. Для примера оценим влияние растворенного в воде вещества на плодовитость дафний, используемых в качестве тест-объектов в водно-токсикологических экспериментах. В ходе предварительного исследования были получены четыре выборки, четыре группы значений плодовитости животных, выращенных в средах с разным содержанием химической добавки. Сначала необходимо сгруппировать выборочный материал в комбинативную таблицу (организовать дисперсионный комплекс). Для этого варианты каждой выборки записываются в отдельные графы, именуемые градациями (табл. 9). Результативным признаком служит средняя плодовитость дафний за неделю (для иллюстративности расчетов она дана в целых числах). В нашем примере организованы 4 градации – чистая вода (контроль, градация А1; значения плодовитости 6, 5, 5, 7), слабая концентрация вещества (5 мг/л, А2; 8, 7, 6, 6), средняя (15 мг/л, А3; 8, 8, 7) и сильная (30 мг/л, А4; 8, 7, 9). Предлагаемый ниже алгоритм расчетов позволяет использовать неравное число вариант в градациях. Расчеты показаны в таблице 9. Таблица 9
Полученные значения позволяют вычислить дисперсии, определить силу влияния фактора и критерий достоверности Фишера.
Поскольку полученное значение критерия (F= 4.39) больше табличного (F(0.05,3,10) = 3.7) (табл. 7П), отличие факториальной и случайной дисперсий достоверно, влияние фактора значимо. Отсюда следует биологический вывод: стимулирующее влияние изучаемого фактора (вещества) на плодовитость дафний относительно велико (57%) и достоверно (с вероятностью Р > 0.95). Непараметрический однофакторный дисперсионный анализ Рассмотренные выше схемы дисперсионного анализа исходили из предположения о нормальном распределении изучаемого результативного признака. Когда для какого-либо признака нет уверенности, что выполняется предположение о его нормальном распределении, когда требуется провести анализ быстро и без особой точности, когда мало данных или они выражены качественными признаками, можно использовать схему непараметрического дисперсионного анализа. Этот метод более неприхотлив, но менее точен, нежели параметрический анализ. Он исследует распределения вариант в нескольких выборках. Нулевая гипотеза состоит в том, что распределения одинаковы, т. е. выборки взяты из одной генеральной совокупности. Порядок вычислений состоит в том, что все варианты ранжируются в порядке возрастания. Затем суммируются ранги вариант по каждой выборке отдельно и рассчитывается критерий: 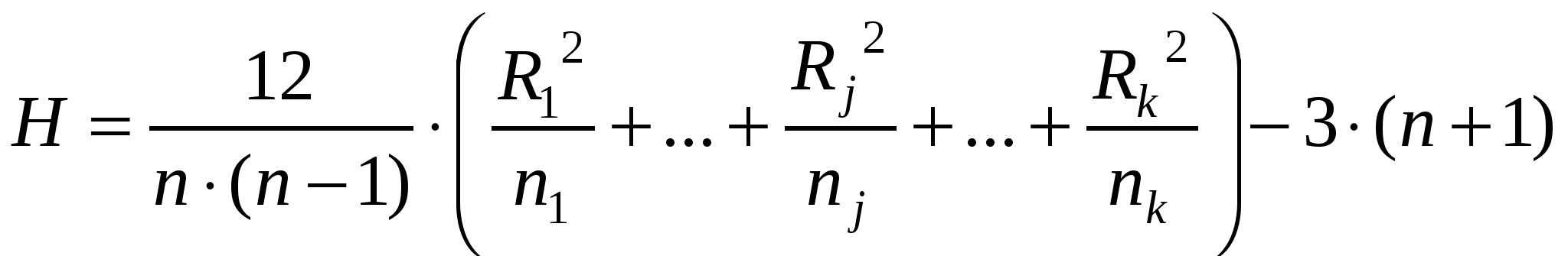 χ²(α,k− 1), χ²(α,k− 1),где n – число всех вариант, nj – объем j-й градации фактора, Rj – сумма рангов для каждой j-й градации фактора, k– число градаций фактора (j= 1, 2, …, k). При объеме выборок больше 5 вариант статистика H имеет распределение хи-квадрат с df = k− 1 степенями свободы и сравнивается со значениями из табл. 9П. Применим эту схему (табл. 10) к нашим данным из табл. 9, расположив их в строку.
Затем упорядочим и ранжируем их. Для нескольких одинаковых значений берется средний ранг.
Наконец, разнесем ранги по градациям и подсчитаем необходимые суммы. Таблица 10
Общий объем выборки равен n = 14. Величина критерия H составит: = 0.065934∙907.8958 – 45 = 14.86. По таблице распределения статистики χ² для α = 0.05 и df = 4 − 1 = 3 находим χ²(0.05, 3) = 7.81. Полученное значение критерия (14.86) больше табличного (7.81), значит, отличие выборочных распределений достоверно. Химическая добавка действительно изменяет плодовитость дафний. Двухфакторный дисперсионный анализ количественных признаков Двухфакторный дисперсионный анализ исследует влияние на результативный признак двух факторов как порознь, так и совместно. Учет эффекта влияния каждого фактора по отдельности теоретически ничем не отличается от описанных выше схем. И там и тут оценивается изменчивость средних по градациям на фоне случайной изменчивости вариант внутри градаций, с помощью критерия Фишера устанавливается достоверность отличий межгрупповых дисперсий от внутригрупповых. Двухфакторный дисперсионный анализ, естественно, требует более сложных вычислительных операций, чем однофакторный, но в принципе ничем не отличается от описанных выше схем. Однако это относится лишь к ортогональным (равномерным, или пропорциональным) комплексам, характеризующимся равной или по крайней мере пропорциональной численностью групп (в градациях содержатся одинаковые или пропорциональные числа вариант). Что же касается неортогональных многофакторных комплексов, то их анализ принципиально возможен, но имеет свои особенности, существенно усложняющие технику вычислений, и в настоящем пособии не рассматривается. На практике вполне допустим и такой способ избегнуть сложностей обработки неравномерных комплексов, как искусственное превращение их в равномерные. Для этого нужно составить выборки одинаковой или пропорциональной численности, используя только часть имеющихся данных. Следует, однако, помнить, что такой отбор не должен быть субъективным. Чтобы не допустить возможной тенденциозности, лучше всего прибегнуть к жеребьевке. Важным преимуществом двухфакторного дисперсионного анализа перед однофакторным служит то, что с его помощью удается определить варьирование по сочетанию градаций Ссочет. = СAB, позволяющее получить новый и весьма ценный в биологическом отношении показатель – оценку влияния сочетанного действия (взаимодействия) факторов. Общая вариация (сумма квадратов) признака теперь состоит из четырех компонентов за счет более детального разложения факториальной дисперсии. Правило разложения вариаций предстает как: Собщ. = СA + СB +СAB + Сслуч., Сфакт. = Собщ.− Сслуч. = СA + СB + СAB. Для расчетов используются следующие смысловые формулы: Собщ. = Σ(xi− M)², СA. = Σ(MAj− M)², j– число градаций фактора А, MAj – групповые средние по градациям фактора А, СB = Σ(MBk− M)², k– число градаций фактора В, MBk– групповые средние по градациям фактора В, Сслуч. = Σ(xi− Mxi)², СAB = Собщ.−(СA + СB + Сслуч.). Сочетанное действие (взаимодействие) каждого из двух факторов проявляется в усилении или ослаблении непосредственного действия другого фактора на объект исследования. К примеру, неурожай кормов усугубляет негативное действие зимнего холода на численность популяций мелких млекопитающих. Рассмотрим числовой пример – испытания стимулятора многоплодия при разной полноценности рационов. Полноценность рациона (первый фактор) представлена двумя градациями: A1 – рацион с недостатком минеральных веществ, А2 – рацион, полностью сбалансированный по всем питательным веществам, включая и минеральные. Стимулятор (второй фактор) был испытан в трех дозах: В1 – одинарная, В2 – двойная, В3 – тройная. Результативный признак – плодовитость самок, измерявшаяся числом детенышей в помете. Для каждого сочетания градаций рациона и стимулятора были подобраны три одновозрастные самки. Комбинативная таблица двухфакторного равномерного дисперсионного комплекса с трехкратной повторностью (ni = 3) включает две градации по фактору А и три градации по фактору В (табл. 11). Варианты размещаются по градациям, определяется объем градации, вычисляются суммы вариант, частные средние, затем вспомогательные величины (Н1, Н2, Н3, НА, НВ) и суммы квадратов отклонений (дисперсий) по рабочим формулам. В завершение всего заполняют таблицу дисперсионного анализа (табл. 12), находят показатель достоверности влияния Фишера и, сопоставляя его с табличным для соответствующих степеней свободы и принятого уровня значимости, делают статистический вывод. Таблица 11
В нашем примере все факториальные влияния оказались достоверными с доверительной вероятностью Р > 0.95 (табл. 12). Это позволяет сделать определенные выводы относительно действия стимулятора на плодовитость самок. Влияние каждого фактора в отдельности (качества рациона и дозы стимулятора) и их суммарного эффекта достаточно существенно, но особенно результативно действие стимулятора в сочетании с полноценным рационом (величина η²АВвыше, чем η²А и η²В). Более того, при недостатке в корме минеральных веществ двукратные и трехкратные дозы стимулятора могут даже снизить плодовитость животных. Таблица 12
Таблица двухфакторного дисперсионного анализа имеет ту же структуру, что и таблица для однофакторного анализа, только факториальная дисперсия разложена на три компоненты (для факторов А, В и их взаимодействия). Для каждой из них требуется вычислить число степеней свободы с учетом числа градаций фактора А (j, количество столбцов) и числа градаций фактора В (k, количество рядов), значения дисперсий, а также критерий Фишера. Поскольку каждому из расчетных значений критерия соответствует свое число степеней свободы, табличные значения окажутся разными. оценка зависимости между признаками Изложенные выше методы статистического анализа дают возможность изучать изменчивость биологических объектов по отдельным признакам – весу, размерам, плодовитости, физиологическим показателям и др. Однако в ряде случаев важно знать, какова зависимость между вариацией двух или нескольких признаков, изменяются ли две переменные самостоятельно, независимо друг от друга, или варьирование одного признака в какой-то степени связано с изменчивостью другого. В качестве второй переменной часто выступает какой-либо фактор среды. Задачу исследования зависимостей можно рассматривать как развитие метода дисперсионного анализа, решающего задачу сравнения нескольких выборок, т. е. изучающего влияния фактора на признак. Техника дисперсионного анализа имеет две особенности. Фактор (или факториальный признак) задан дискретно, в виде градаций, или «доз». Когда исследуется фактор, заданный качественно, то разбиение на градации всего диапазона его действия оказывается очень эффективным способом создания подобия количественной переменной. Но при изучении количественно заданного фактора в грубой градуальной схеме дисперсионного анализа утрачивается часть информации, которая содержится в исходных выборках и которую можно было бы использовать. Кроме этого, дисперсионный анализ явным образом не учитывает тенденции изменения среднего уровня признака при изменении уровня фактора, не содержит показателя характера (знака) зависимости признака от фактора. Все эти «недостатки» дисперсионного анализа не характерны для методов изучения сопряженной изменчивости – корреляционного и регрессионного анализов. Способ представления отдельных наблюдений здесь меняется: каждая варианта рассматривается как носитель двух численных характеристик объекта измерения, двух зависимых значений случайной величины. Если выше мы отождествляли отдельное значение с отдельной вариантой, то теперь мы рассматриваем варианту как некоторое тело, обладающее минимум двумя зарегистрированными качествами, различными у разных вариант:  Например, для любого животного можно определить массу (M) и длину (L) тела; отдельная варианта будет нести два значения (L, M). При этом множество вариант выборки можно отобразить графически как точки на плоскости осей двух признаков M и L. Вся выборка предстанет в виде множества точек на плоскости (двумерное рассеяние). Как видно на диаграмме (рис. 10), «облако» вариант вытянуто в направлении диагонали облака точек. Справа вверху находятся варианты с высокими значениями и размеров и массы тела, в левом нижнем углу – с наименьшими значениями. В центре расположены варианты с промежуточными, средними значениями. 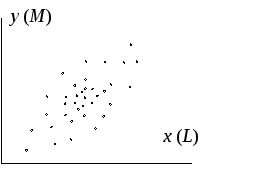 Рис. 10. Область рассеяния вариант В первом приближении можно сказать, что двумерное распределение –это ординация вариант на плоскости осей двух признаков. Помимо рассеяния на плоскости, в определение двумерного распределения входит и частота встречаемости отдельных значений (a). Если признаки x и y теоретически подчиняются нормальному закону, тогда скопление вариант в трех осях (оси признаков x, yи частоты а) образует весьма странный «гребень», растянутое в пространстве выпуклое нормальное распределение (рис. 11). Однако в реальности такой идеальной картины получить никогда не удается, приходится ориентироваться только на плоскую фигуру рассеяния немногочисленных вариант. Если область, занятую вариантами, очертить по периферии плавной линией, мы получим вытянутую фигуру, эллипс, ограничивающий область рассеяния вариант, эллипс рассеяния. Эллипс рассеяния – это область распространения вариант одной совокупности. М 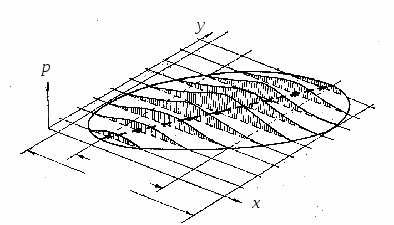 ожно видеть, что в нашем примере признаки связаны друг с другом – есть общая тенденция: чем больше длина тела, тем больше вес; эта зависимость не очень жесткая, она размыта индивидуальными особенностями объектов (вариант). ожно видеть, что в нашем примере признаки связаны друг с другом – есть общая тенденция: чем больше длина тела, тем больше вес; эта зависимость не очень жесткая, она размыта индивидуальными особенностями объектов (вариант). Рис. 11. Двумерное распределение В двумерном распределении проявляются два эффекта: синхронное изменение двух признаков и размывание этой синхронности, т. е. действие факторов сопряжения признаков вдоль оси эллипса и действие случайных факторов – поперек нее. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
