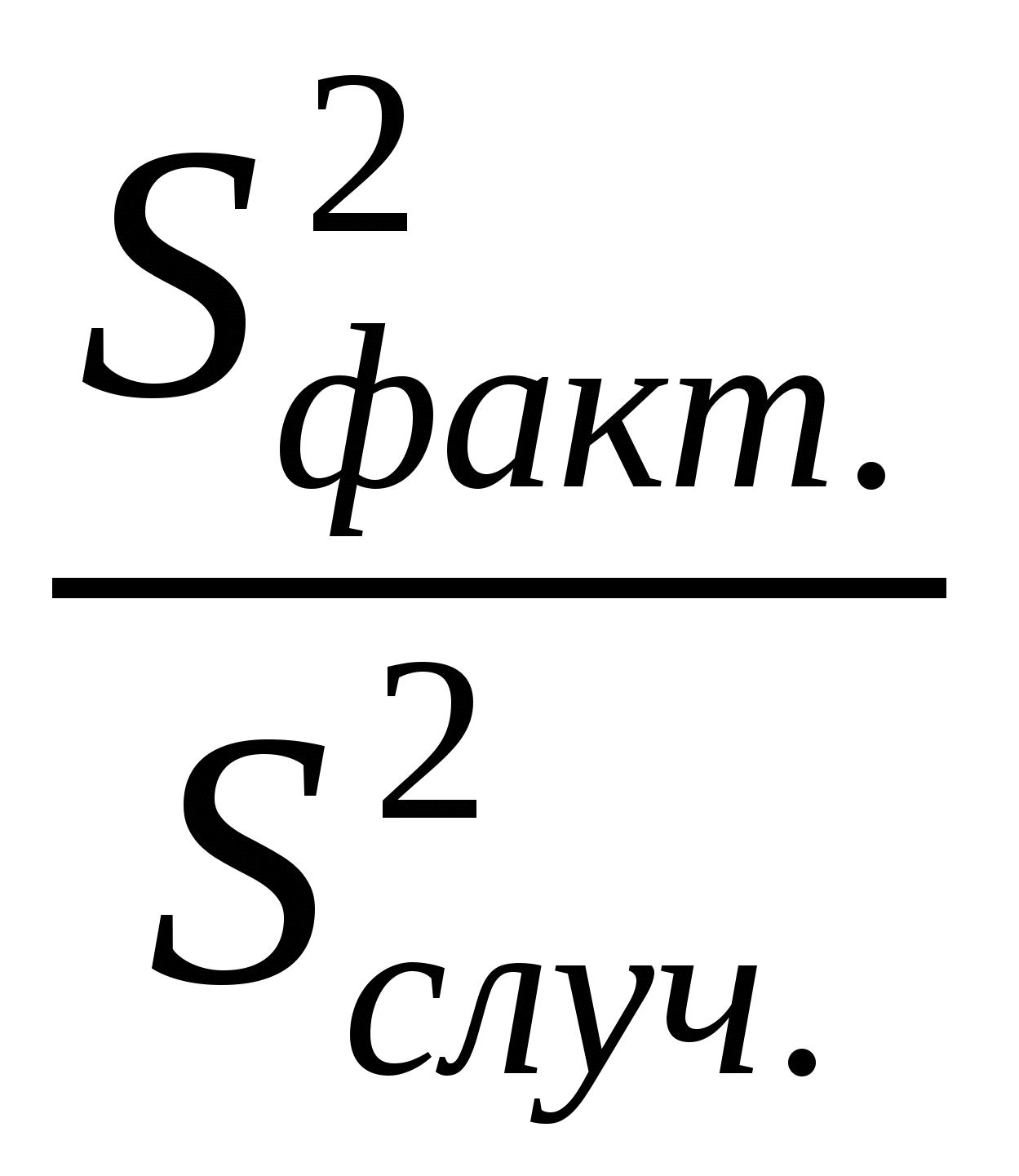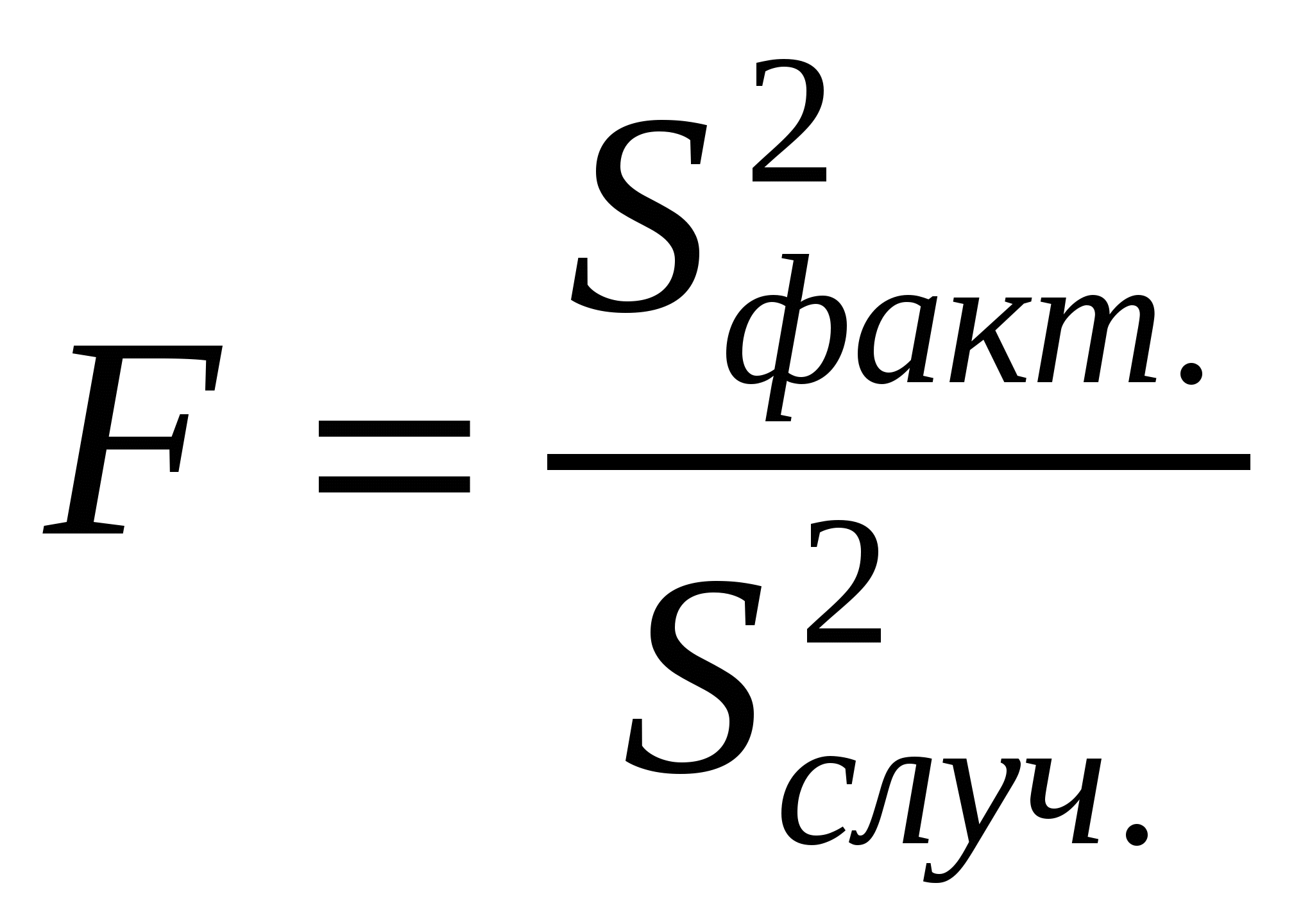|
|
Элементарная биометрия. Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях
оценка влияния фактора
При изучении и анализе сложных и многообразных причинно-следственных отношений между объектами и явлениями биологу приходится учитывать целый комплекс внешних и внутренних факторов, от которых в конечном итоге зависят уровень и ход наблюдаемых процессов, те или иные биологические свойства живых организмов, их динамика и разнообразие. При этом зачастую важно оценивать не только роль одного из многочисленных внешних факторов, но и их взаимодействие при констелляционном влиянии на популяцию или организм.
Идейная база для изучения действия факторов содержится уже в методе сравнения двух выборок. Биологическим содержанием операции сравнения двух выборок, в конце концов, выступает поиск факторов, ответственных за смещение средних арифметических или усиление изменчивости признаков. Развивая это направление биометрического исследования, можно не ограничиваться только двумя «дозами» фактора, но изучить серию ситуаций, в которых фактор проявлял разную силу действия на результативный признак – от самого слабого до самого сильного. При этом каждому уровню фактора будет соответствовать отдельная выборка и общая задача получит формулировку «сравнить несколько выборок». В терминах факториальной биометрии вопрос о влиянии фактора на признак звучит так: сказывается ли отличие условий получения разных выборок на качестве (значениях) вариант? В терминах статистики вопрос звучит несколько иначе: из одной ли генеральной совокупности отобраны все выборки, оценивают ли выборочные средние арифметические одну и ту же генеральную среднюю? Вариантов ответа может быть только два:
Все выборки отобраны из одной генеральной совокупности, условия возникновения вариант одни и те же.
Выборки отобраны из разных генеральных совокупностей, условия возникновения вариант выборок различаются.
В постановке вопроса можно уловить противоречие. Выше было сказано, что по условию задачи выборки формировались в разных условиях, и тут же предполагается, что условия были одинаковые. На самом деле противоречия нет, поскольку речь идет об определении чувствительности признака к действию фактора. Условия формирования выборок могут отличаться, но они могут никак и не сказаться на величине изучаемого признака, не отразиться на значениях вариант. Смысл статистического сравнения в том и состоит, чтобы оценить эффективность действия фактора на признак, доказать реальность реакции вариант выборок на разные условия их формирования. В сферу исследования можно вовлекать как один, так и два признака, как количественные, так и качественные характеристики. В каждом случае процедура анализа несколько отличается.
Однофакторный дисперсионный анализ количественных признаков
Дисперсионный анализ позволяет оценить степень и достоверность отличия нескольких выборочных средних одновременно, т. е. изучить влияние одного контролируемого фактора на результативный признак путем оценки его относительной роли в общей изменчивости этого признака, вызванной влиянием всех факторов. Сущность дисперсионного анализа заключается в расчленении общей вариации (дисперсии) изучаемого признака, вычисляемой по сумме квадратов отклонений отдельных вариант (x) от средней арифметической всего комплекса наблюдений (М), на его составные части –дисперсию, вызванную организованными, учитываемыми в исследовании факторами (факториальную дисперсию), оценивающую межгрупповую изменчивость, и дисперсию, обусловленную остальными, неорганизованными в данном исследовании факторами (внутригрупповую, или случайную, дисперсию) отклонения отдельных значений от средней в группе.
Общая вариация (сумма квадратов) признака рассчитывается как сумма квадратов отклонений всех вариант (xi) от общей средней (M):
Собщ. = Σ (xi− M)².
Факториальная (межгрупповая, межвыборочная) сумма квадратов рассчитывается как сумма квадратов отклонений частных средних (Mi) для каждой выборки (всего k выборок) от общей средней:
Сфакт. = Σ (Mj− M)².
Остаточная (случайная, внутригрупповая) сумма квадратов есть сумма квадратов отклонений вариант каждой выборки (xi) от своей средней (Mj):
Сслуч. = Σ (xi−Mj)².
Очевидно, что в общем комплексе наблюдений должно выполняться равенство Собщ. = Сфакт. + Сслуч.
Отношение сумм квадратов к соответствующему числу степеней свободы дает оценку величины дисперсии, или средний квадрат, иногда ее именуют варианса. Влияние изучаемого фактора отражает факториальная, или межгрупповая, дисперсияS²факт., а влияние случайных неорганизованных в данном исследовании причин – случайнаяS²случ., или внутригрупповая, остаточная дисперсия S²остат.:
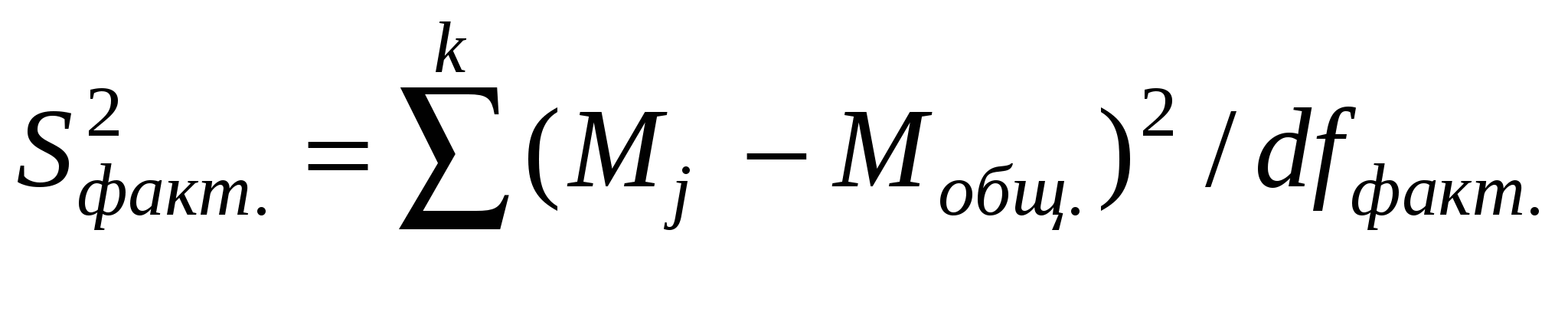 , ,
где dfфакт. = k− 1, j= 1, 2, …, k, k – число сравниваемых средних.
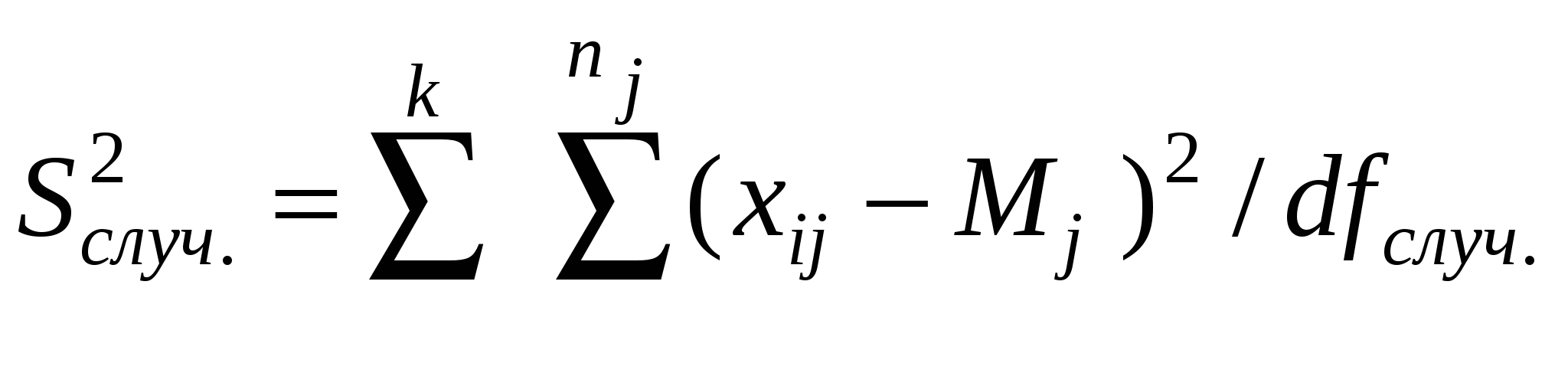 , ,
где df случ. = n − 1, i= 1, 2, …, n, n – число вариант всех выборок.
Сила влияния фактора определяется как доля частной суммы квадратов в общем варьировании признака. Показатель силы влияния изучаемого фактора составляет: η²факт. = Сфакт. / Собщ., неорганизованных (случайных): η²случ. = Сслуч. / Собщ.; сумма этих показателей, естественно, равна единице: η²факт. + η²случ. = 1. Заметим, что показатель силы влияния дисперсионного комплекса есть не что иное, как квадрат пирсоновского корреляционного отношения, которым и оценивается относительная доля влияния организованного (изучаемого) фактора в общем суммарном статистическом влиянии всех факторов, определяющих развитие данного результативного признака.
О достоверности оценок влияния факторов судят по уже знакомому нам критерию Фишера: 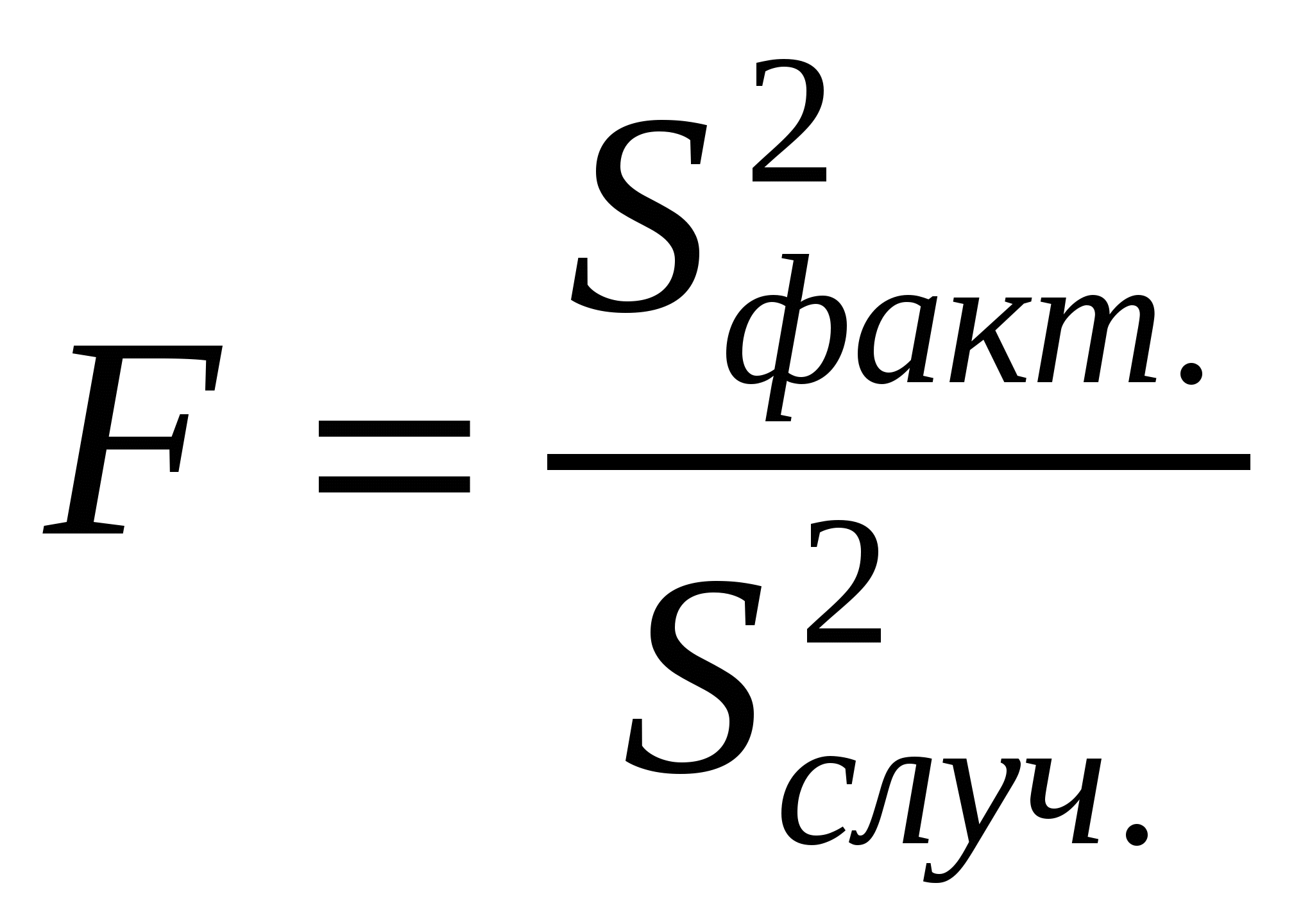
F(α, df1, df2),
где df1 = k − 1, df2 = n − k, k – число градаций,
n – общий объем всех выборок.
Проверяется нулевая гипотеза: «влияние фактора на признак отсутствует». Влияние считается доказанным, если величина расчетного критерия равна или превышает свое табличное значение с принятым уровнем значимости (обычно α = 0.05) (F определяется по табл. 7П). Все параметры однофакторного дисперсионного анализа и порядок их вычислений представлены в таблице 8.
Таблица 8
Составляющие дисперсии
| Суммы квадратов (SS), С |
Сила влияния,
η²
|
Степени свободы,
df
|
Дисперсии
(средний квадрат, MS),
S²
|
Критерий влияния,
F |
Факториальная
|
Сфакт. =
Σ (Mj− M)²
|
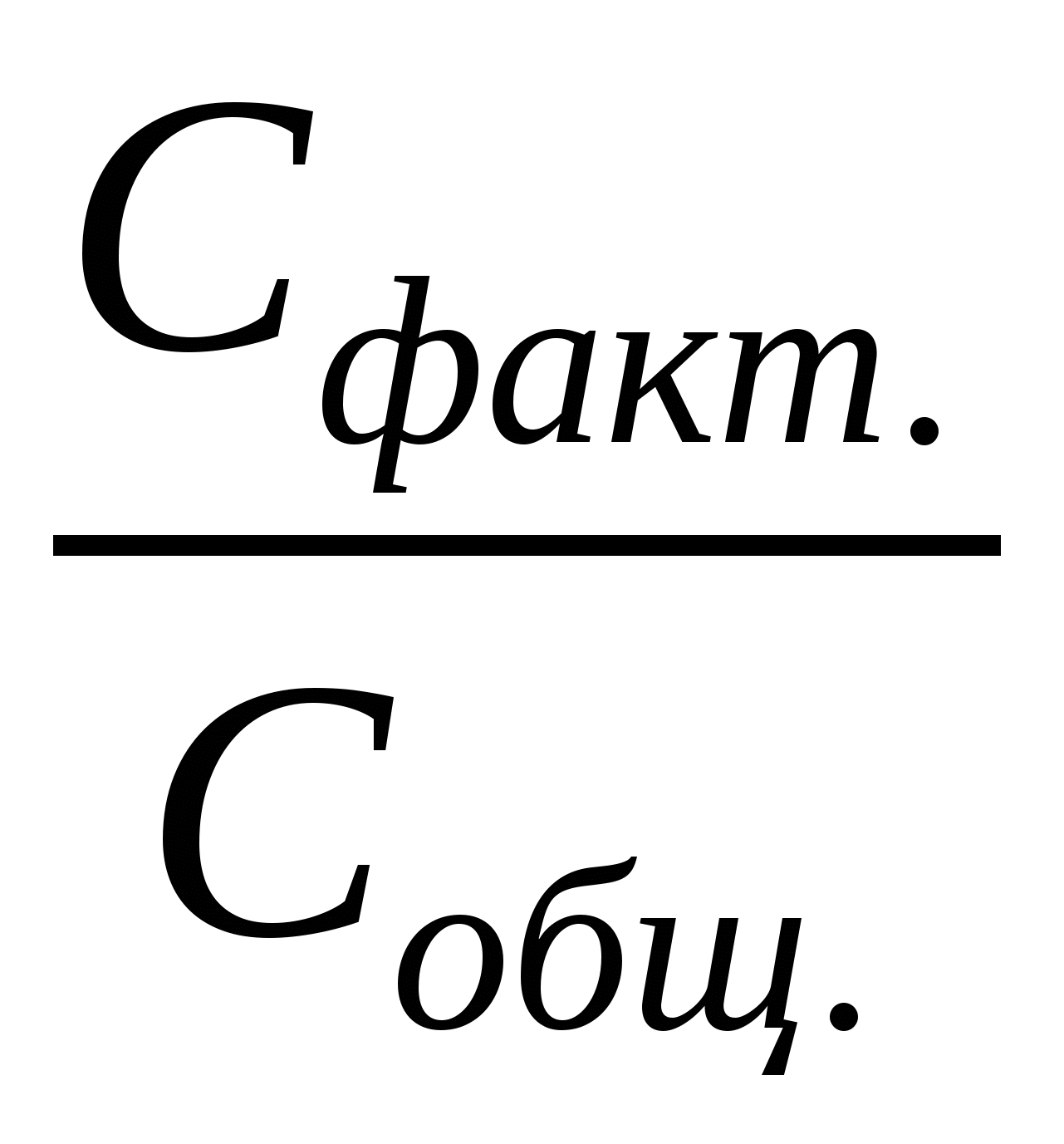
|
k− 1
|
S² факт. =
= 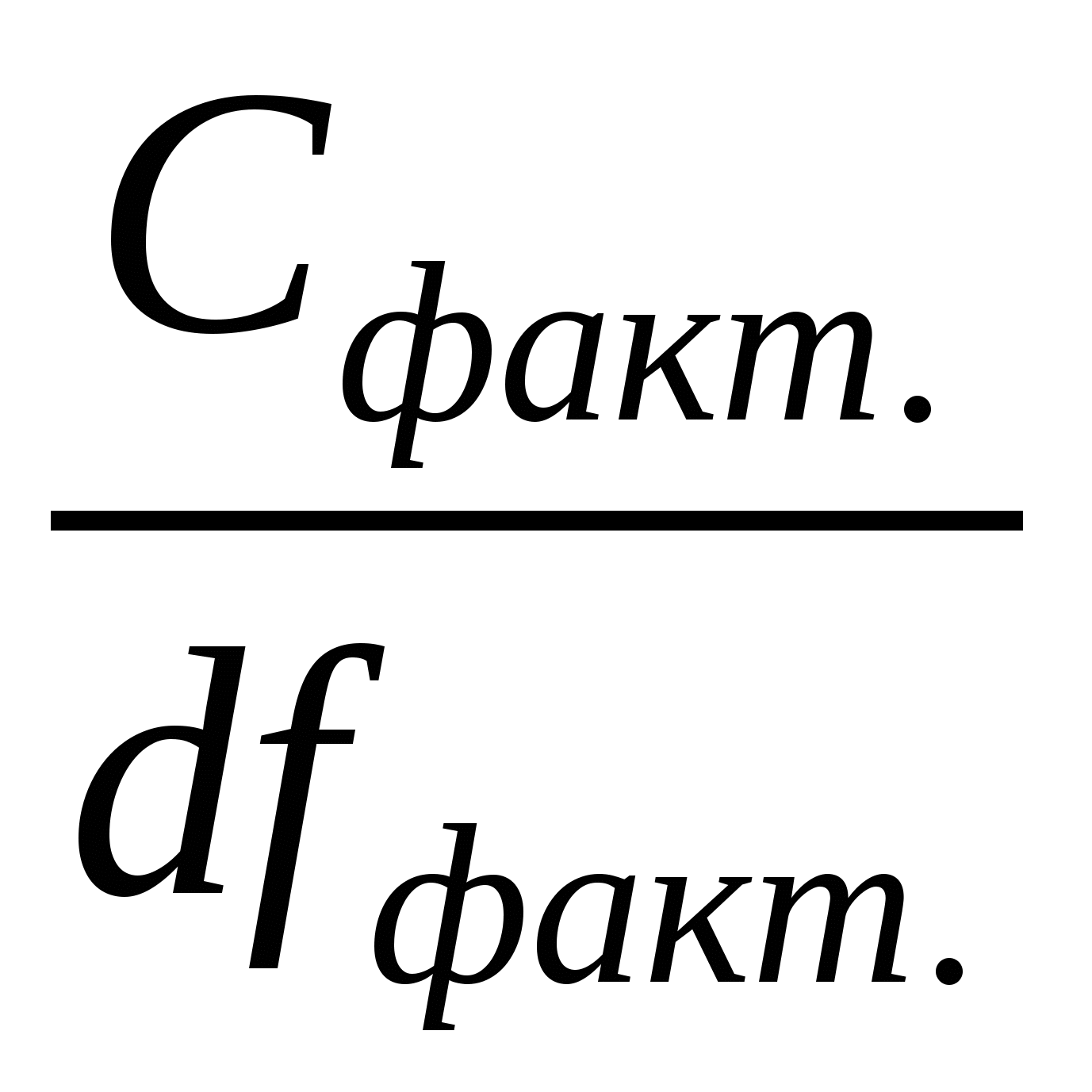
|
F =
|
Случайная
|
Сслуч. =
Σ (xi− Mj)²
|
|
n− k
|
S²случ. =
= 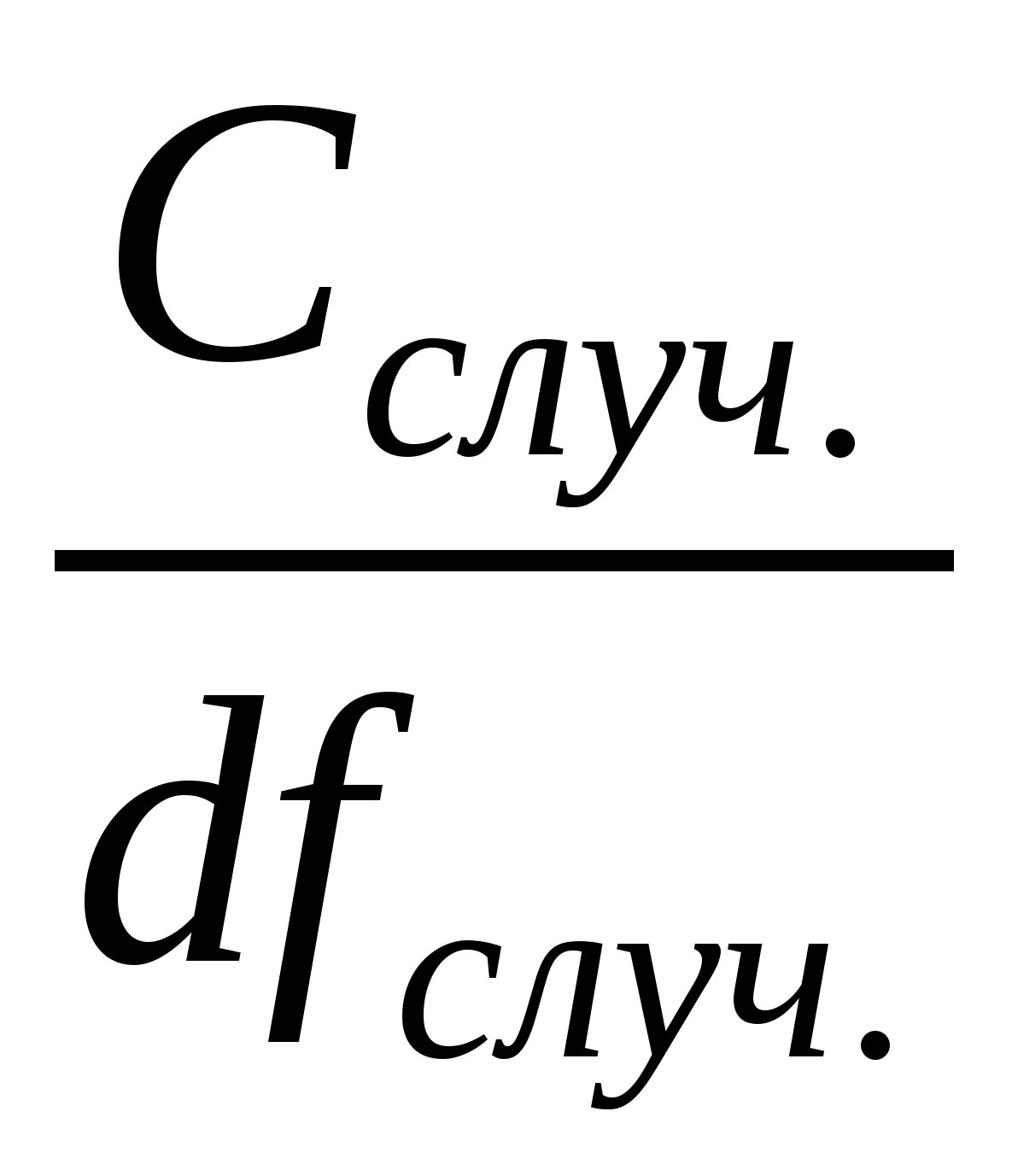
|
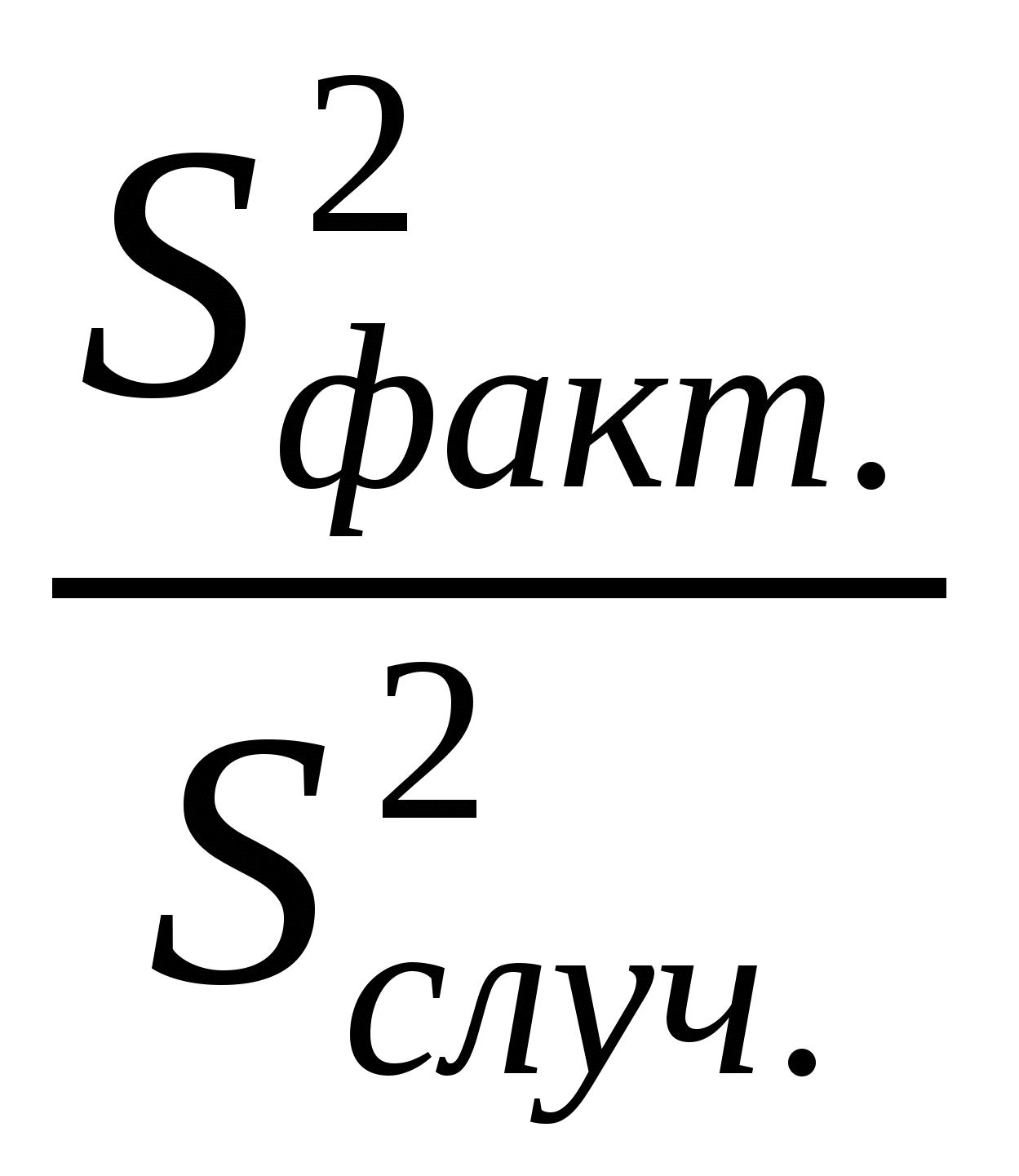
|
Общая
|
Собщ. =
Σ (xi− M)²
|
|
|
|
| |
|
|
 Скачать 3.04 Mb.
Скачать 3.04 Mb.