Элементарная биометрия. Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях
 Скачать 3.04 Mb. Скачать 3.04 Mb.
|
Криволинейная регрессияВ большинстве случаев связь биологических признаков не бывает линейной, они изменяются либо с разной скоростью, либо в разных масштабах. Соответственно на графике форма такой связи отображается не прямой, а кривой линией. Примерами могут служить геометрическая прогрессия роста численности популяции в оптимальных условиях, различие скоростей роста разных частей тела, определяющее аллометрический характер зависимости признаков (лицевой отдел черепа растет более интенсивно, чем мозговой). В подобных случаях эффективнее использовать не уравнения прямой линии (у = ах+b), а разнообразные уравнения кривых линий, например, степенной, гиперболической, экспоненциальной, параболической, логистической и др. Поскольку метод наименьших квадратов исходно ориентирован на линию (поиск уравнения линии, наименее удаленной ото всех эмпирических точек), прямой расчет уравнений кривых в рамках регрессионного анализа невозможен. Натурные данные необходимо предварительно «выпрямить», т. е. сделать возможным вычисление линейного уравнения регрессии с тем, чтобы потом из него получить уравнение криволинейной связи. Общий порядок регрессионного анализа для криволинейной зависимости следующий:
Рассмотрим процесс поиска уравнения криволинейной регрессии на примере изучения зависимости веса печени прыткой ящерицы от длины ее тела (рис. 16). Рассчитанное по исходным данным уравнение линейной регрессии имеет вид: у = 107.9х − 404.2. И хотя коэффициент регрессии достоверен (t= 7.6, α < 0.05) и коэффициент детерминации высок R² = 0.866, это уравнение весьма приблизительно описывает зависимость признаков – для наименьших наблюдаемых значений длины тела оно дает абсурдное (отрицательное) значение массы печени (107.9∙3.4 − 404.2 = −37.3 мг). Линейная модель не годится даже для интерполяции изучаемых данных. Гораздо успешнее справляется с подобной задачей степенная (аллометрическая) функция у= bxa. 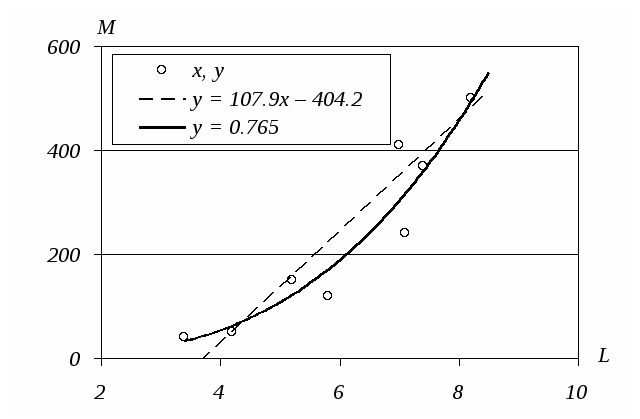 ∙x3.07 0.765∙x3.07 Рис. 16. Зависимость веса печени (M, мг) от длины тела (L, мм) у ящериц Для вычисления коэффициентов этого уравнения воспользуемся преобразованием: Y= lgy, X= lgx, B= lgb. После логарифмирования степенное уравнение приняло линейный вид: lgy= lgb + a∙lgx илиY= B+aX. Теперь остается отыскать коэффициенты уравнения B и a, используя алгоритм метода наименьших квадратов (табл. 19). Таблица 19
Далее рассчитаем суммы, необходимые промежуточные значения и коэффициенты (расчеты выполнялись в среде Excel): ΣY= Σlgy= 20.6, ΣY² = Σ(lgy)² = 48.64, ΣX= Σlgx= 7.043, ΣX² = Σ(lgx)² = 5.659, ΣXY= Σ(lgx∙lgy) = 16.577, MY = ΣY / n = 20.6 / 9 = 2.289, MX = ΣX / n = 7.043 / 9 = 0.7826, CXY = ΣXY − (ΣX)∙(ΣY) / n = 16.572 − 7.043∙20.602 / 9 = 0.45542, CX = ΣX² − (ΣX)² / n = 5.655 − (7.04)² / 9 = 0.14816, CY = ΣY² − (ΣY)² / n = 48.638 − (20.601)² / 9 = 1.4823, a= CXY / CX= 0.45541 / 0.14815 = 3.0739, B= MY −aMX= 2.289 − 3.0739∙0.7826 = −0.11643. Линейное уравнение для преобразованных данных имеет вид: lgy= 3.07∙lgx+ lg(−0.116) или Y' = 3.07∙X− 0.116. Это уравнение дает возможность рассчитать теоретические значения признака Y' (теоретические значения логарифмов массы печени), квадраты отклонений прогнозных значений от реальных: (Y' − Y)², а также их сумму Σ(Y' − Y)² = 0.08239. Эта величина есть остаточная сумма квадратов; вместе с общей суммой квадратов Cy= Cобщ. = 1.4823 она позволяет сформировать таблицу дисперсионного анализа (табл. 20): Смод. = Собщ. − Состат. = 1.4823 − 0.08239 = 1.39993. Таблица 20
Полученное значение F= 118 больше табличного (5.6), следовательно, дисперсия, обусловленная регрессией, достоверно больше случайной, т. е. признак Y действительно зависит от признака X, и линия регрессии адекватна исходным данным. Коэффициент детерминации больше, чем у линейной регрессии, и составляет: R² = Срегр. / Собщ. = 1.399 / 1.4823 = 0.944. Ошибка коэффициента криволинейной регрессии равна: а критерий Стьюдента, проверяющий гипотезу Но: a = 0, составляет t= a / ma = 3.0739 / 0.281 = 10.9. Полученное значение (10.9) больше табличного (t(0.05, 8) = 2.31 для уровня значимости α = 0.05 и числа степеней свободы df = n− 2 = 8), коэффициент регрессии a значимо отличается от нуля; зависимость признака Y от X есть, причем очень тесная. Следует помнить, что при расчете ошибки коэффициента криволинейной регрессии используются стандартные отклонения для преобразованных (у нас – прологарифмированных) значений признаков. В завершение выполним обратное преобразование второго коэффициента регрессии, свободный член равен: b= 10B= 10−0.11643 = 0.764839. Теперь уравнение регрессии принимает вид степенной зависимости: у'= 0.765∙x3.07. Теоретические значения у', рассчитанные по этому уравнению, гораздо ближе к исходным данным, что хорошо видно и на графике (рис. 16), и по большей величине коэффициента детерминации (0.94 > 0.87) (читателю несложно будет проделать все вычисления в среде Excel с помощью программы Регрессия – как для исходных, так и для преобразованных данных). Аллометрическое уравнение (у'= 0.8х3) не только лучше описывает зависимость между признаками в статистическом плане, но и придает ей более ясный биологический смысл (масса печени = 0.8∙длина тела3). Как известно, объемные величины (объем, масса тела) пропорциональны кубу линейных промеров (длина тела). В свою очередь, вес печени и вес тела связаны прямой пропорциональной зависимостью. Так становится понятной наблюдаемая прямая пропорциональность веса печени кубу длины тела. ВМЕСТО послесловия В конце книги авторы посчитали полезным поместить практически неизвестное широкому читателю стихотворное произведение «Гайавата ставит эксперимент», принадлежащее перу одного из самых крупных мировых авторитетов в области математической статистики – Мориса Дж. Кендалла. На первый взгляд оно достаточно далеко от традиционного жанра научной публикации, но на самом деле не только остроумно, иронично и талантливо само по себе, но и весьма точно отражает, разъясняет и иллюстрирует суть наиболее актуальных и сложных дискуссионных проблем современной вариационной статистики. Уж лучше Великого Кендалла обо всем этом, разумеется, не скажешь! Предлагаемая вниманию читателей поэма впервые увидела свет на страницах журнала «American statistic» (1959, № 13) и воспроизводится в поэтическом переводе А. Дмоховского (см. Ричард Беллман «Процессы регулирования с адаптацией»: Пер. с англ. М.: Наука, 1964). ГАЙАВАТА СТАВИТ ЭКСПЕРИМЕНТ 1 Всюду славен Гайавата, Он стрелок непревзойденный. Легкий лук он поднимает – Десять стрел взмывают к небу, И последняя слетает С тетивы тугой, звенящей Прежде, чем вонзится в землю Первая из десяти. Все, кто видел Гайавату, Говорили, что бесспорно Совершенства он достиг. 2 Но какой-то хитрый скептик Тем не менее заметил, Что в стрельбе не только ловкость, Но и меткость ценят люди. И добавил: было б лучше, Если б славный Гайавата В цель попал бы хоть однажды, Пусть хоть выборка при этом Будет меньшего объема. 3 Гайавата рассердился И сказал, что он в колледже Посвятил себя науке, Что статистикой зовется, Он себя считая вправе Поучать своих собратьев, Тут же лекцию прочел им. Вспомнил он закон ошибок, Усеченные кривые, Информации потерю, Заявил, что он добился Несмещенных результатов, И сказал, что после многих Независимых попыток, Даже если в их итоге В цель ни разу не попал он, – Все равно по средней точке Отклонений от мишени Можно сделать твердый вывод, Что стрелял он безупречно (За возможным исключеньем Пресловутой меры нуль). 4 Но упрямые индейцы Возразили Гайавате, Что они не понимают Столь туманных рассуждений. Им совсем не интересен Результат его попыток. И они предполагают, Что охотник должен метко В цель стрелять. А если будет Он впустую тратить стрелы – Должен сам за них платить. 5 Раздраженный Гайавата Стал цитировать обильно Р. А. Фишера и Итса, Приводить работы Финни, Книги Кемпторна Оскара, Главы Кокрана и Кокса, Андерсена и Банкрофта. Он взывал к авторитетам, Убеждая несогласных, Что в стрельбе всего важнее Не прямое попаданье, А научно безупречный Статистический подход. 6 Кое-кто из возражавших Согласился с Гайаватой, Что в подобной точке зренья Есть, возможно, доля смысла, Но, пожалуй, все же лучше Не пускаться в рассужденья, А без промаха стрелять. 7 Наш герой в ответ на это Предложил за луки взяться, Чтоб строптивых оппонентов В правоте своей уверить. Он сказал: «Необходимо Так построить состязанье, Как советует учебник Проводить эксперименты». (Хоть научный этот способ Применяется обычно Для проверки качеств чая, Но порою, как известно, Приложим к другим вещам.) Гайавата разработал Точный план соревнований, Чтоб случайный их порядок В соответствие пришелся С тем характером, который Носят множители в славной Той теории, что ныне Носит имя Галуа. 8 Те, кто выразил готовность Состязаться с Гайаватой, Были круглые невежды В проведеньи испытаний, И поэтому, наверно, Все оставшееся время Проводили в тренировках, Соревнуясь меж собою Или просто в цель стреляя. 9 И во время состязанья Результаты всех стрелявших Были просто превосходны, Но, увы, за исключеньем (Как ни трудно мне признаться) Результата Гайаваты. Гайавата, как обычно, Вверх свои направил стрелы. Он так ловко это сделал, Что остался несмещенным, Но при этом, к сожаленью, В цель ни разу не попал. 10 «Что ж, – сказали тут индейцы, – Мы иного и не ждали». 11 Гайавата, не смущаясь, Попросил перо, бумагу, Произвел расчет дисперсий И в итоге вывел цифры, Из которых стало ясно, Что стрелки смогли добиться Лишь смещенных результатов, И дисперсии при этом Одинаковыми были И совсем не отличались От дисперсии, которой Гайавата сам достиг. (Правда, следует отметить, Что последний этот вывод Убедительнее был бы, Если б в данных Гайаваты, По которым вычислял он Результат эксперимента, Зафиксированы были И прямые попаданья. К сожаленью, оппоненты, В вычислениях не смысля, Не смогли с героем спорить, Что бывает очень часто При анализе дисперсий.) 12 Тем не менее индейцы, Не поверившие цифрам, Отобрали у героя Легкий лук его и стрелы И сказали, что, возможно, Гайавата в самом деле Выдающийся статистик, Но при этом совершенно Бесполезен как стрелок. Что ж касается дисперсий, То какой-то грубый неуч Произнес такое слово, Что его, сказать по чести, В статистическом изданьи Я не смею повторить. 13 И теперь в лесу дремучем Бродит грустный Гайавата. Непрестанно размышляя, Вспоминает он нормальный Тот закон распределенья Отклонений и ошибок, Что лишил его навеки Славы лучшего стрелка. И порою он приходит К трезвой мысли, что наверно Нужно целиться точнее, Несмотря на риск смещенья, Если все же в результате Иногда ему удастся Поражать стрелою цель. Список рекомендуемой лИТЕРАТУРЫ Адлер Ю. П., Макарова Е. В., Грановский Ю. В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976. Ашмарин И. П. и др. Быстрые методы статистической обработки и планирования экспериментов. Л.: Изд-во ЛГУ, 1975. Бейли Н. Статистические методы в биологии. М.: Мир, 1964. Браунли К. А. Статистическая теория и методология в науке и технике. М.: Наука, 1977. Гроссман С., Терней Дж. Математика для биологов. М.: Высшая школа, 1983. Гублер Е. В., Генкина А. А. Применение непараметрических критериев статистики в медико-биологических исследованиях. Л.: Медицина, 1973. Дэвис Дж. Статистический анализ данных в геологии: В 2 кн. М.: Недра, 1990. Животовский Л. А. Популяционная биометрия. М.: Наука, 1991. Зайцев Г. Н. Математический анализ биологических данных. М.: Наука, 1981. Зайцев Г. Н. Математика в экспериментальной ботанике. М.: Наука, 1990. Ивантер Э. В., Коросов А. В. Введение в количественную биологию. Петрозаводск, 2003. Коросов А. В. Экологические приложения компонентного анализа. Петрозаводск, 1996. Лакин Г. Ф. Биометрия. М.: Высшая школа, 1973. Плохинский Н. А. Биометрия. М.: Изд-во МГУ, 1970. Поллард Дж. Справочник по вычислительным методам статистики. М.: Финансы и статистика, 1982. Рокицкий П. Ф. Биологическая статистика. Минск: Вышейшая школа, 1973. Тюрин Ю. Н., Макаров А. А. Статистический анализ данных на компьютере. М.: ИНФРА, 1998. Урбах В. Ю. Биометрические методы. М.: Наука, 1964. Урбах В. Ю. Статистический анализ в биологических и медицинских исследованиях. М.: Медицина, 1975. Фишер Р. Статистические методы для исследователей. М.: Госстатиздат, 1958. Приложение Справочные таблицы Таблица 1П |
