Элементарная биометрия. Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях
 Скачать 3.04 Mb. Скачать 3.04 Mb.
|
Этапы биометрического исследованияБиометрия помогает биологам обнаружить «закономерности». Закономерное – это повторяющееся, причем в известных условиях. Математическая статистика, исследующая массовые проявления, служит средством доказательства существования той или иной закономерности, причинной обусловленности серии фактов. Факт сам по себе, раз случился, достоверен. Доказывать приходится реальность существования причин, вызвавших факты к жизни и тем самым обеспечивающих их общность. Биометрия служит необходимым средством достижения биологом своих целей, установленных исходя из существа биологической проблемы. В этом смысле для биометрического исследования очень важна точная формулировка биологического вопроса. При этом спланировать способ обработки фактических данных нужно загодя, еще перед их сбором! Только в этом случае можно максимально эффективно решить проблему. 1. Определить объект исследования. Объект исследования – это не вид животного или растения, это исследуемый феномен со всеми относящимися к делу внешними компонентами, включая пространство (распространение) и время (динамика). Объектом частного биологического исследования выступает ограниченная во времени и пространстве биосистема. 2. Определить проблему (и актуальность) исследования. Проблема («Что плохо?») в научном плане есть отсутствие знаний об объекте исследования в определенной области его биологии. Потребность в недостающей информации появляется в том случае, когда уже имеются некоторые данные, обрисовывающие границы известного и обнажающие края неизвестного. 3. Определить цель исследования. Цель («Чего хочется?») в обобщенном виде характеризует итог исследования. Только на этом фоне возможны обобщения на больших территориях и временах, т. е. обнаружение неких закономерностей. Цель служит постоянным критерием эффективности выполненных действий, основой рефлексии, ограничителем. 4. Определить задачи исследования. Задачами («Что сделать?») отмечаются шаги к цели, это мост между ней и конкретными средствами ее достижения. Задачи – это руководства к действию, указания, как делать и что будет получено в результате, если предпринять такие-то действия. На этом этапе выясняется объем массивов собираемой информации, вид количественных характеристик (переменных), их число, способы регистрации статуса объектов измерения и факторов среды, схемы опытов и т. п. Знание этих частностей необходимо, чтобы запланировать использование того или иного статистического метода, предъявляющего свои требования к исходным данным. Точнее всего работают параметрические методы, но они требуют регистрации количественной информации в форме рациональных или натуральных чисел. Если же запланировать получение характеристик объектов в приблизительных полуколичественных шкалах (баллы, ранги) или только качественных признаков, то следует иметь в виду, что в конце концов придется пользоваться более грубыми непараметрическими методами статистики. 5. Сбор и накопление данных, изучение биологического явления. При сборе данных важно помнить правило «единообразия и равновероятности» собираемых выборок, чтобы свести к минимуму субъективные и систематические ошибки, уменьшающие точность измерений. Это условие относится к способу формирования выборок, суть которого заключается в создании одинаковых условий наблюдения и обеспечении равной вероятности получаемых результатов: каждая варианта должна иметь возможность представлять весь спектр действующих факторов без ограничений; в противном случае состав выборки будет не гомогенным и статистические законы будут проявляться «неправильно», что сделает невозможным применение точных статистических критериев. 6. Решение биометрической задачи. Статистические методы требуют жесткой определенности формулировок. Чтобы добиться требуемой строгости, исходно рыхлое словесное описание биологического вопроса предварительно необходимо перевести на язык методов математической статистики, после чего выполнить расчетные процедуры и в завершение получить требуемый ответ. Процедура решения биометрической задачи включает несколько этапов. Конкретизация. Формулирование биологической задачи, требующей статистического решения, обозначение объекта исследования, характеристика условий (факторов, методов) получения выборки, явное определение отдельной варианты (объекта измерения) и всей выборки вариант. Формализация. На этом этапе требуется дать ответы на два вопроса общего характера. Ответ на вопрос «Что доказать?» помогает явно назвать один из четырех типов биометрических задач: доказать чужеродность варианты (классификация), доказать отличие двух выборок (сравнение), доказать влияние фактора (множественное сравнение), доказать зависимость признаков (выявление тренда). Ответ на вопрос «Что описать?» заставляет сделать выбор того обобщенного показателя, который интересует исследователя: описание может касаться величины признака (оценивается средней), его изменчивости (оценивается дисперсией), распределения частот (выражается вариационным рядом), выборки в целом (выражается совокупностью ранжированных вариант). Выбор вида статистической задачи. Именно здесь отчетливее всего проявляются уровень биометрической подготовки исследователя, его профессионализм и мастерство, наконец, чутье на адекватный статистический метод. В этом смысле биометрия выступает как своеобразное искусство постановки статистической задачи. Вместе с тем многие биологические задачи решаются по принципу аналогии. Это позволяет предложить «Определитель статистического метода», несколько формальных критериев подбора адекватного статистического приема (табл. 1). Выдвижение нулевой гипотезы. Если первые два этапа осуществляли постановку биологической задачи, то третий призван дать четкую статистическую формулировку поставленного вопроса. Нулевая гипотеза (Н0) – это гипотетическое предположение об отношениях объектов, выраженное в терминах статистики и предназначенное для дальнейшей статистической проверки. В самой общей форме нулевая гипотеза звучит так: «Отличия недостоверны». Согласно нулевой гипотезе, наблюдаемые отличия, например, двух выборок являются случайными, различия между выборочными параметрами есть ошибки репрезентативности; в действительности обе выборки вместе составляют один и тот же однородный материал и принадлежат к одной генеральной совокупности. Таблица 1
В процессе статистического анализа нулевая гипотеза либо отвергается (опровергается, отклоняется), и тогда различия считаются достоверными, либо принимается (сохраняется). Последнее, однако, не означает доказательства случайности различий (их отсутствия), а лишь говорит о том, что при данном объеме и качестве материала различия остаются недоказанными. Опираясь на полученный в процессе научной работы материал, статистика способна лишь доказать выдвинутые гипотезы или же отсеять и отвергнуть те предположения, для которых недостаточно информации, отделить, как зерна от плевел, истинные отличия от случайных, привнесенных неучтенными факторами, вычленить реальную закономерность из обилия сырого экспериментального материала. Решение по алгоритму. Выполнение расчетов с помощью выбранного метода. Чтобы избежать возможных ошибок при «ручном счете», необходимо придерживаться нескольких правил. Так, арифметические ошибки нетрудно выявить, если еще до начала расчетов ориентировочно прикинуть ожидаемый результат. Для этого полезно дважды пересчитывать рабочие формулы, меняя местами слагаемые и сомножители. При использовании стандартных формул целесообразно вначале выписать их в символьной форме и лишь затем подставлять числовые значения. Очень важно также не путать сумму квадратов (Σx²) с квадратом суммы ((Σx)²) вариант, объем выборки (n) с числом градаций или групп (k). Лучше всего формировать таблицы вычислений по приведенным в книге алгоритмам. Полезно проверять схождение сумм по строкам и столбцам, а вычисленных величин – по модели анализа. Например, при вычислении критерия хи-квадрат сумма частот эмпирического распределения должна точно совпадать с суммой теоретических частот. Подозрение на допущенную ошибку должны вызывать отрицательные суммы квадратов (за исключением регрессионного и корреляционного анализов) и минусовые значения критерия Стьюдента (его всегда берут по модулю), величины критерия, в десятки и сотни раз превышающие табличные, а также несовпадение величины исходного признака с рассчитанным по регрессионной модели. Наконец, следует помнить, что если «на глаз» распределение количественных признаков приближается к нормальному, то стандартное отклонение примерно равно четверти от всего размаха выборки: S≈ (max − min)/ 4. Только распределение Пуассона имеет равные среднюю и дисперсию (M≈ S²). Статистический вывод. Статистический вывод, главный результат статистического анализа, – это заключение о справедливости или опровержении нулевой гипотезы. Строится он на основе сравнения полученной (эмпирической) величины статистического критерия с табличной (теоретической). Если расчетная величина больше табличной, говорят о достоверном отличии параметров (о влиянии, об исключении), т. е. об опровержении нулевой гипотезы. Если же вычисленные значения критерия меньше табличного, нулевая гипотеза остается в силе, отличия не считаются достоверными (значимыми). На практике для правильного статистического вывода можно воспользоваться упрощенной схемой сравнения эмпирических значений критерия с табличными (рис. 1). Числа 0.95 и 0.05 – это доверительная вероятность и уровень значимости (вероятность правильности или неправильности вывода). Разместив в этой схеме табличные и эмпирические значения критериев, нетрудно заметить, что вычисленная величина лежит правее табличной, в критической области, а это говорит о достоверности отличий сравниваемых параметров, в данном случае двух средних арифметических. Сказанное можно проиллюстрировать следующим примером. Пусть при сравнении двух средних арифметических нулевая гипотеза состояла в том, что отличие средних арифметических случайно. В расчетах было получено значение критерия T = 3.5. Табличная величина для этого случая равна T = 2.1. Поскольку полученное значение критерия (3.5) больше табличного (2.1), можно утверждать, что эти средние арифметические достоверно отличаются. Слово «достоверно» значит буквально «статистически доказано»: отличие двух сравниваемых средних и без того бросалось в глаза, но лишь статистическое доказательство показало реальность этих различий, позволило распространять конкретный вывод на все явление. Критерий доказал, что отличие средних не случайно, а закономерно. 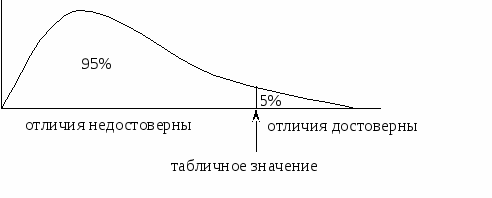 Рис. 1. Схема использования критериев. Отмечены критические зоны для уровней значимости α = 0.05 и α = 0.01 (доверительные вероятности Р = 0.95 и Р = 0.99). Границами зон служат значения критериев из таблиц Приложения при данном уровне значимости. Если вычисленные величины критерия попадают в критическую зону (правее табличных), значит, отличие сравниваемых параметров достоверно Ответ на вопрос. Формулируется биологическое утверждение, доказанное статистически. Если удалось доказать достоверность неких отличий, то для биолога принципиально важна их направленность, не только факт отличий, например, средних арифметических, но и как именно они отличаются, какая величина превышает другую. Биологический ответ есть, по существу, перифраза статистического вывода, «одетого» в биологические термины и поэтому приобретающего биологический смысл и содержание. 7. Биологическая интерпретация результатов обработки. Если статистический вывод не отвергает нулевую гипотезу, то важных с биологической точки зрения заключений сделать нельзя. Сохранение гипотезы о случайности отличия показателей не дает нам полную уверенность в том, что их действительно нет. Возможно, в нашем распоряжении просто оказалось недостаточно данных, чтобы сделать достоверный вывод. Может быть, исследование следует по-иному спланировать и повторить. Если же статистический анализ выявил достоверность отличия, это дает основание сформулировать более содержательное и убедительное биологическое заключение, в частности, рассматривать выявленные отличия как результат действия какого-то систематического фактора, интерпретировать зависимость как биологическую закономерность, говорить об особых свойствах «выпадающей» из совокупности варианты (объекта). | ||||||||||||||||||||||||||||||||||||||||||||||||
