Элементарная биометрия. Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях

• Название: Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях
• Анкор: Элементарная биометрия.doc
• Дата: 04.01.2018
• Размер: 3.04 Mb.
• Имя файла: Элементарная биометрия.doc
• Тип: Книга; #13667
• страница: 7 из 32

статистическая оценка генеральных параметров

Биометрия изучает поведение биологических случайных величин, которые точно не предсказуемы, хотя и не абсолютно случайны. В этом разделе будут рассмотрены способы определения диапазона возможной изменчивости изучаемых биологических признаков. Приблизительный прогноз всегда можно дать в виде интервала между конкретными минимальными и максимальны­ми значениями, в пределах которого будет находиться интере­сующая нас величина. Ясно, например, что рост очередного встречного взрослого человека вряд ли пре­высит два метра или будет меньше полутора метров. Более точный (вероятностный) прогноз можно дать, ориентируясь на распределение случайных величин. Распределение – это соотно­шение между значениями случайной величины и частотой их встречаемости. Как мы видели на примере веса тела землероек, числовые значения вариант располагаются в некоторой ограниченной зоне, в цент­ре которой их особенно много, а по краям мало. Ключом к получению вероятностного прогноза служит знание законов распределения случайных величин. Очень большое число случайных величин, распространенных в природе, может быть описано с помощью закона нормального распределения, который задается уравнением: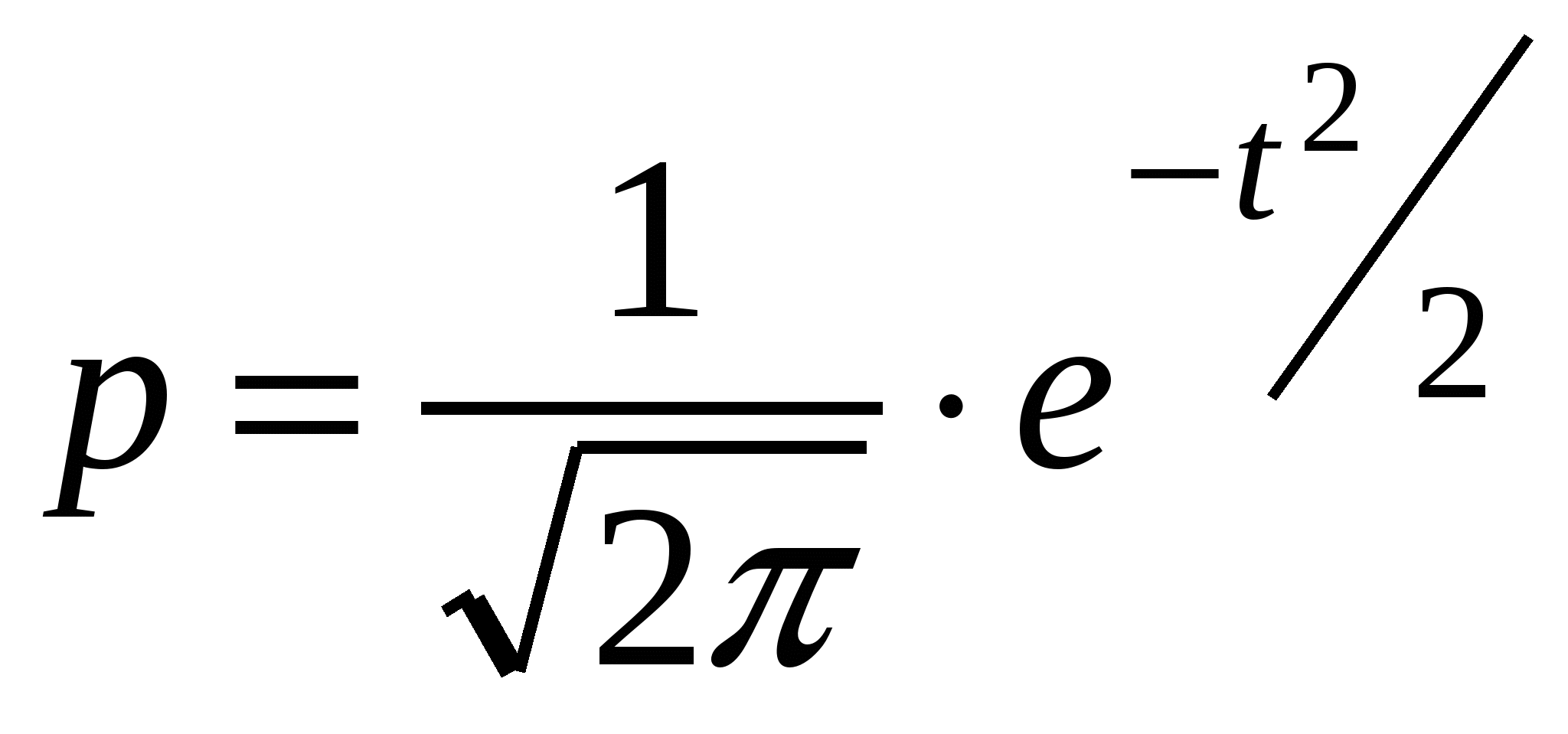

,

где – нормированное отклонение;

M, S – параметры нормального распределения.

Эта модель лежит в основе многих статистических методов.

Свойства нормального распределения

Приведенное уравнение определяет ход кривой линии, имеющей характерную колоколообразную форму, и позволяет вычислить ординаты нормальной кривой, или «плотность вероятности» (p). Вероятность (статистическая, или частость) – численная мера возможного, определяется как отношение числа вариант (исходов испытаний) определенного вида к общему числу вариант (опытов). Поскольку нормальное распределение характерно для непрерывных случайных величин, говорят не о вероятности какого-то определенного значения варианты, но о «плотности вероятности», отражая тем самым плавность изменения вероятности значений для разных значений t, чем ближе к центру распределения, тем плотность вероятности выше.

С помощью представленного выше уравнения можно рассчитать вероятность появления нового значения случайной величины t в интервале той или иной ширины и дать статистическую оценку – найти интервал значений признака, в котором с той или иной вероятностью заключено значение генерального параметра. Формула количественно выражает вполне определенные свойства поведения случайной величины, из которых можно назвать следующие практически важные следствия:

1. Все варианты лежат в интервале плюс-минус беско­нечность. Иными словами, с вероятностью P = 1 (P = 100%) мы вправе ожидать появление новой варианты в пределах от −∞ до +∞. Слева и справа от средней арифметической лежит по 50% вариант (свойство симметрии нормального распределения), т. е. с вероятностью P = 0.5 (50%) можно предска­зать появление новой варианты в интервалах M − ∞ и M + ∞.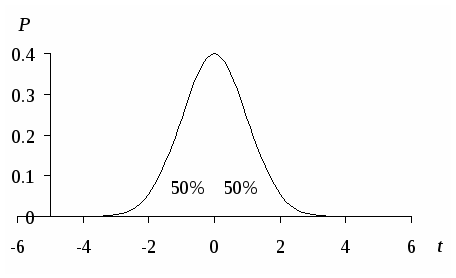



2. Между M − 1.96S и М + 1.96S лежит 95% вариант. Это позволяет с 95%-ной вероятностью предполагать, что новая варианта окажется в интервале М ± 1.96S (округленно М ± 2S – так называемое правило двух стандартных отклонений).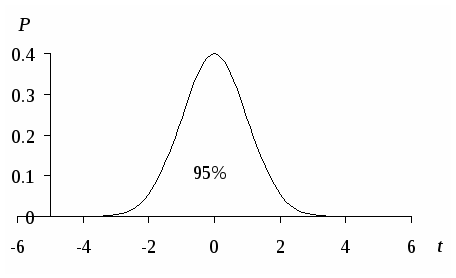



3. С вероятностью P = 0.99 значение новой варианты бу­дет заключено в пределах М ± 2.58S и с вероятностью P = 0.999 – в интервале М ± 3.3S.
Исходя из сказанного можно оценить вероятность появле­ния новых значений признака. В отношении непрерывных слу­чайных величин (метрических признаков) эта процедура сво­дится к так называемой интервальной оценке. Для полученных ранее характеристик, массы бурозубок, средней M= 9.26 и стандартного отклонения S= 0.79 (г), находим прогнозный интервал: M± 1.96S= 9.26 ± 1.53. Новое значение признака с вероятностью P = 0.95 меж­ду 7.68 и 10.82 г. Предсказание веса землероек, конечно, не имеет большого практического значения. Гораздо важнее может быть прогноз численности ценных промысловых видов, сельскохозяйственных вредителей, вспышек болезней, урожая культур­ных растений и т. п.

Важнейшее значение для практического применения имеет «соглашение о 95%». В соответствии с ним совокупности, состоящей из 95% особей (объектов), мы доверяем так же, как и 100%-й. Термин «доверительная вероятность P = 0.95» означает, что, согласно принятому допущению, 95% вариант достаточно полно характеризуют изучаемое явление (в данном случае изменчивость веса землероек), что позволяет ограни­читься рассмотрением вариант в области М ± 1.96S, охватываю­щей эту 95%-ю совокупность. Так, мы принимаем, что нормальный вес землероек данного вида может изменяться в пределах 7.7–10.8 г, не больше и не меньше. За этими пределами мы обнаруживаем животных иного вида или статуса.

При этом в биометрии обычно довольствуются доверительной вероятностью P = 0.95 (уровень значимости α = 0.05), хотя в наиболее ответственных исследованиях принимают и более строгие уровни – P = 0.99 и P = 0.999. Однако это имеет смысл лишь при очень больших выборках исходных данных, точно описывающих закономерности изменчивости признаков. Обычно же выборки не очень велики, что позволяет ограничиться меньшей степенью доверительной вероятности Р = 0.95.

Уровень значимости – понятие, альтернативное довери­тельной вероятности и, соответственно, его величина составляет разность между единицей и значением доверительной вероятности (α = 1 − P). Для доверительной вероятности 0.95 уро­вень значимости составляет 0.05, а для 0.99 и 0.999 – соответ­ственно 0.01 и 0.001. Уровень значимости, равный 0.05 (5%), можно интерпретировать так: имеется всего 5% шансов, что полученная величина не будет соответствовать изучаемой со­вокупности. Уровень значимости – это тот теоретический про­цент значений нормального распределения, который можно от­бросить, не учитывать, дабы с меньшими усилиями получить основную информацию об изучаемом явлении. Можно целую жизнь положить на попытки отловить обыкновенную землеройку-бурозубку весом 2.5 г, но так и не собрать выборку, доста­точную по объему, чтобы это реализовать (миллионы особей). Для практического понимания достаточно знать, что уровень значимости – это приблизительная вероятность ожидаемой ошибки наших вы­водов. И с этой позиции 5% – достаточно мало. Использование доверительной вероятности и уровня значимости можно назвать теоретической базой разумного ограничения времени и масштабов ис­следования, позволяющей получить достоверную общую ин­формацию за счет исключения ничтожной доли частной.

Генеральная совокупность

Генеральная совокупность – все варианты одного типа. В предметной биологии это понятие можно интерпретировать как мыслимое множество вариант, сформированных при одинаковых (внешних и внутренних) условиях.

Теоретическая бесконечность генеральной совокупности означает, что ее никогда нельзя познать до конца, в действительности мы всегда имеем дело с выборками. Выборочная совокупность, выборка – это множество вариант одного типа, ограниченное способом отбора (методами получения вариант) из генеральной совокупности. Отличие выборок от генеральной совокупности состоит в том, что действующие в генеральной совокупности факторы не могут проявиться в полной мере в любой отдельной выборке. Каждая новая выборка обязательно будет отличаться от предыдущей в силу случайности, варианты новой выборки будут нести одинаковый отпечаток действия доминирующих факторов, но разные следы действия случайных факторов. По этой причине параметры (средняя M и стандартное отклонениеS) разных выборок из одной генеральной совокупности никогда не совпадут ни друг с другом, ни со значениями генеральных параметров (обычно обозначаемых буквами μ, σ), они будут немного отличаться, смещаясь относительно друг друга и варьируя вокруг генеральных значений.

Отличие генеральных параметров от их оценок по выборкам состоит еще и в том, что в первом случае они рассчитаны по всем вариантам, а во втором – по ограниченному их числу. Интуитивно понятно, что, чем меньше объем выборок, тем менее точным будут выборочные оценки генеральных параметров и, напротив, чем больше выборка, тем ближе выборочные средние и дисперсии лежат к генеральным значениям. Это явление называется закон больших чисел – с ростом числа наблюдений значения выборочных параметров стремятся воспроизвести генеральные.