Элементарная биометрия. Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях

• Название: Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях
• Анкор: Элементарная биометрия.doc
• Дата: 04.01.2018
• Размер: 3.04 Mb.
• Имя файла: Элементарная биометрия.doc
• Тип: Книга; #13667
• страница: 8 из 32

Ошибка репрезентативности выборочных параметров

По части никогда не удается полностью охарактеризовать целое, всегда остается вероятность того, что выборочная оценка недостаточна близка к значению параметра генераль­ной совокупности, имеет некоторую ошибку. Отличия значений выборочных параметров от генеральных называются ошибкой репрезентативности данного параметра, или просто (статистической) ошибкой. При уве­личении объема выборки ошибки репрезентативности стремятся к нулю (следствие закона больших чисел). Численно выраженные статистические ошибки служат мерой тех пределов, в которых выборочные параметры могут отклоняться от значений генеральных параметров. Например, если для нескольких выборок, полученных из одной и той же генеральной совокупности, посчитать средние, а затем оценить изменчивость этих средних, то стандартное отклонение средних (S_M) и будет численной мерой ошибки репрезентативности выборочной средней. Она обозначается буквой m.

Величина ошиб­ки тем больше, чем больше варьирование признака (S) и чем мень­ше выборка (n). Ошибку репрезентативности имеют все статистические параметры, рассчитанные по выборке. Для практики статистического оценивания разработаны специальные формулы. Для нормального распределения они имеют следующий вид. Ошибка средней: ,

ошибка стандартного отклонения: ,

ошибка коэффициента вариации: .

Вычисленные значения ошибок подставляют к соответствую­щим параметрам со знаками плюс-минус (параметр ± ошибка) и в такой форме представляют в научных отчетах и публика­циях. В примере с бурозубками для разных параметров имеем:

, M = 9.3 ­­± 0.11 г,

, S = 0.89 ± 0.079 г,

, CV = 9.6 ± 0.9%.

Не следует путать статистическую ошибку с методическими ошибками и ошибками точности (точности измерений, анализов, подсчетов и т. д.), хотя методические погрешности и увеличивают ошибку репрезентативности, но другим путем – методические огрехи увеличивают изменчивость признака, стандартное отклонение.

При всей неиз­бежности статистической ошибки она может быть сведена к ми­нимуму отбором достаточного числа особей (вариант). С ростом объема выборки оценки параметров стабилизируются, а их ошибки репрезентативности уменьшаются.

Доверительный интервал

П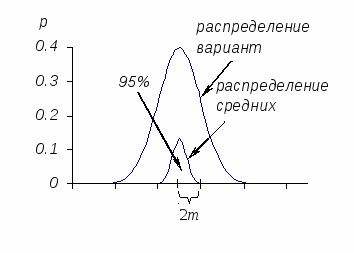араметры генеральной совокупности практически всегда остаются не­известными, о них судят по выборочным оценкам, используя для этого значения ошибок репрезентативности. Теоретические исследования поведения выборочных средних (как случайных величин) показали, что они подчиняются нормальному закону, большинство из них (95%) находится поблизости от генеральной средней – в диапа-зоне M_ген. ± 1.96m (приближенно ±2­m). Это обстоятельство позво-ляет делать обратное заключение – генеральная средняя находится в диапазоне M_выбор. ± 1.96m, т. е. предсказывать ширину интервала, в котором заключен генеральный параметр, давать интервальную оценку генеральному параметру.
В соответствии с законом нормального распределения можно ожидать, что генеральный параметр (истинное значение) окажется в ин­тервале

от М − tm до М + tm,

где m – ошибка средней арифме­тической,

t – квантиль распределения Стьюдента (табл. 6П) при данном числе степеней свободы (df)и уровне зна­чимости (обычно α = 0.05).

Сказанное можно перефразировать так: с вероятностью Pможно ожидать, что генеральная средняя находится в доверительном интервале М ± tm, построенном вокруг выборочной средней арифметической M.

Доверительный интервал – интервал значений изучаемого признака, в котором с той или иной вероятностью P находится значение генерального параметра.

Возвращаясь к примеру о весе землероек-бурозубок, мы теперь можем записать доверительные интервалы при разных уровнях вероятности (граничные значения t взяты для случая n = ∞):

для Р = 0.95 М ± tт = 9.3 ± 1.96 ∙ 0.11 = 9.3 ± 0.21 г;

для Р = 0.99 М ± tт = 9.3 ± 2.58 ∙ 0.11 = 9.3 ± 0.28 г.

Здесь искомая генеральная средняя величина веса землероек с вероятностью P = 95% находится в пределах 9.11-9.53 г, а при P = 99% – 9.04-9.6 г.

Если объем выборки, для которой были получены параметры и ошибка репрезентативности m, был невелик (n< 50), то необходимо вводить поправки на объем выборки, расширяя область возможного пребывания генерального параметра. Это понятно, поскольку при дефиците информации любые заключения не могут быть очень точными. Так, для выборки объемом n = 20 экз. ошибка средней составит г, а доверительный интервал: М± tт = 9.3 ± 2.09∙0.2 = 9.3 ± 0.41 г – от 8.9 до 9.7 г (при уровне значимости α = 0.05 и числе степеней свободы df= n − 1 = 20 − 1 = 19 табличная величина статистики Стьюдента равна t = 2.09).

Аналогичным образом можно построить доверительный интервал для стандартного отклонения (S ± tm_S), коэффициента вариации (CV ± tm_CV), а также других статистических параметров (коэффициентов асимметрии, эксцесса, регрессии, корреляции).