Элементарная биометрия. Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях

• Название: Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях
• Анкор: Элементарная биометрия.doc
• Дата: 04.01.2018
• Размер: 3.04 Mb.
• Имя файла: Элементарная биометрия.doc
• Тип: Книга; #13667
• страница: 5 из 32

Вычисление параметров выборок

Средняя арифметическая

Одной из важнейших обобщающих характеристик вариаци­онного ряда является средняя величина признака (обычно обознача­ется буквой М). Существует несколько видов средних (сред­няя арифметическая – простая и взвешенная, средняя гармо­ническая, средняя квадратичная), но в практике биологических исследований наибольшее значение имеет средняя арифметиче­ская – величина, вокруг которой «концентрируются» варианты.

Общая формула для определения величины средней ариф­метической – это отношение суммы значений всех вариант (x_i) выборки к их числу (объему выборки, n):

.

В нашем примере с определением массы бурозубок средняя величина равна M= 9.298412698 г. При расчетах статистических параметров на ЭВМ следует помнить, что большое количество значащих цифр обычно не имеет никакого биологического смысла. Записывая такие статистические параметры, как средняя и стандартное отклонение, следует оставлять в лучшем случае на одну значащую цифру больше, чем имели значения вариант, а оценки ошибок – на две значащих цифры. Масса тела бурозубок колебалась от 7.3 до 11.9 г, отсюда средняя с учетом округления должна иметь вид M= 9.3 г.

Средняя арифметическая характеризует действие только систематических факторов, поскольку сумма случайных отклонений влево и вправо от средней в силу симметричности нормального распределения обращается в нуль. Поэтому модель варианты меняется: x_i = M ± x_случ.

В биологических исследованиях зачастую встречается ситуа­ция, когда требуется первичная статистическая обработка большого числа выборок, но необязательно с большой точностью. Это может понадобиться для предварительного рас­смотрения и оценки материала, в частности для оперативного выявления общих тенденций его изменчивости, с тем, чтобы в дальнейшем перейти к специальным методам статистического анализа. Для этих слу­чаев предложен простой экспресс-метод с использова­нием полученного для данной выборки размаха значений (Lim). В случае нормального распределения средняя арифметическая находится точно по центру (совпадает со значением медианы), т. е. левая и правая границы распределения находятся на одинаковом расстоянии от средней. Исходя из этих соображений, среднюю арифметическую можно рассчитать по формуле медианы:



Для бурозубок эта средняя составит M = (7.3 + 11.9) / 2 = 9.6 г, что вполне соответствует первой точной оценке.

В случаях, когда необходимо объединить результаты расчетов по нескольким выборкам и на этой основе найти общую среднюю, характеризующую весь изученный материал, пользуются взвешенной средней, которая учитывает объемы частных выборок:

,

где M_j – значение частной средней,

n_j – условные «веса» частного значения, объемы выборок.

Чтобы рассчитать среднюю взвешенную, необходимо значения всех частных средних арифметических помножить на свои «веса», все эти произведения сложить и сумму разде­лить на сумму весов (общий объем всех выборок). Пусть получены результаты определения средней величины выводка у рыжих полевок (экз./ самку) по месяцам: май 5.0, июнь 5.4, июль 6.2, август 6.0, сентябрь 4.5, причем известно число определений (самок) для каждого месяца: 22, 43, 103, 33 и 5. Взвешенная средняя арифметическая составит:

M= (5∙22 + 5.4∙43 + 6.2∙103 + 6∙33 + 4.5∙5) / (22 + 43 + 103 + 33 + 5) = 5.8.

Средняя, рассчитанная обычным спо­собом, оказалась заниженной:

М = (5 + 5.4 + 6.2 + 6 + 4.5) / 5 = 5.4.

В число прочих констант вариационного ряда входит медиана (Me) – значение, делящее размах выборки пополам, и мода (Mo) – класс (или значение), представленный наибольшим числом вариант.
Стандартное отклонение

Среднее квадратичное отклонение (или стандартное отклонение) – вторая по значению константа вариаци­онного ряда. Она является мерой разнообразия входящих в груп­пу объектов и показывает, на сколько в среднем отклоняются варианты от средней арифметической изучаемой совокупности. Чем сильнее раз­бросаны варианты вокруг средней, чем чаще встречаются край­ние или другие отдаленные классы отклонений от средней ва­риационного ряда, тем большим оказывается и среднее квад­ратичное отклонение. Стандартное отклонение есть мера изменчивости признаков, обусловлен­ная влиянием на них случайных факторов. Квадрат стандартного отклонения (S²) называется дисперсией.

Что такое «случайное» при детальном рассмотрении? В формуле модели вариант случайный компонент предстает в виде некой «добавки» к доле варианты, сформированной под действием систематических факторов, ± x_случ.. Она, в свою очередь, складывается из эффектов влияния неопределенно большого числа факторов: x_случ. = Σx_случ.k.

Каждый из этих факторов может обнаружить свое сильное действие (дать большой вклад), а может почти не участвовать в становлении конкретной варианты (слабое действие, незначительный вклад). Причем доля случайной «прибавки» для каждой варианты оказывается различной! Рассматривая, например, размеры дафний, можно увидеть, что одна особь крупнее, другая мельче, поскольку одна родилась на несколько часов раньше, другая позже, или одна генетически не вполне идентична прочим, а третья росла в более прогреваемой зоне аквариума и т. д. Если эти частные факторы не входят в число контролируемых при сборе вариант, то они, индивидуально проявляясь в разной степени, обеспечивают случайное варьирование вариант. Чем больше случайных факторов, чем они сильнее, тем дальше будут раз­бросаны варианты вокруг средней и тем большим оказывается характеристика варьирования, среднее квад­ратичное отклонение. В контексте нашей книги термин «случайное» есть синоним слова «неизвестное», «неподконтрольное». Пока мы каким-либо способом не выразим интенсивность фактора (группировкой, градацией, числом), до тех пор он останется фактором, вызывающим случайную изменчивость.

Смысл стандартного отклонения (вариант от средней) выражает формула:

,

где x – значение признака у каждого объекта в группе,

М – средняя арифметическая признака,

п – число вари­ант выборки.

Выполнять расчеты удобнее с помощью рабочей формулы: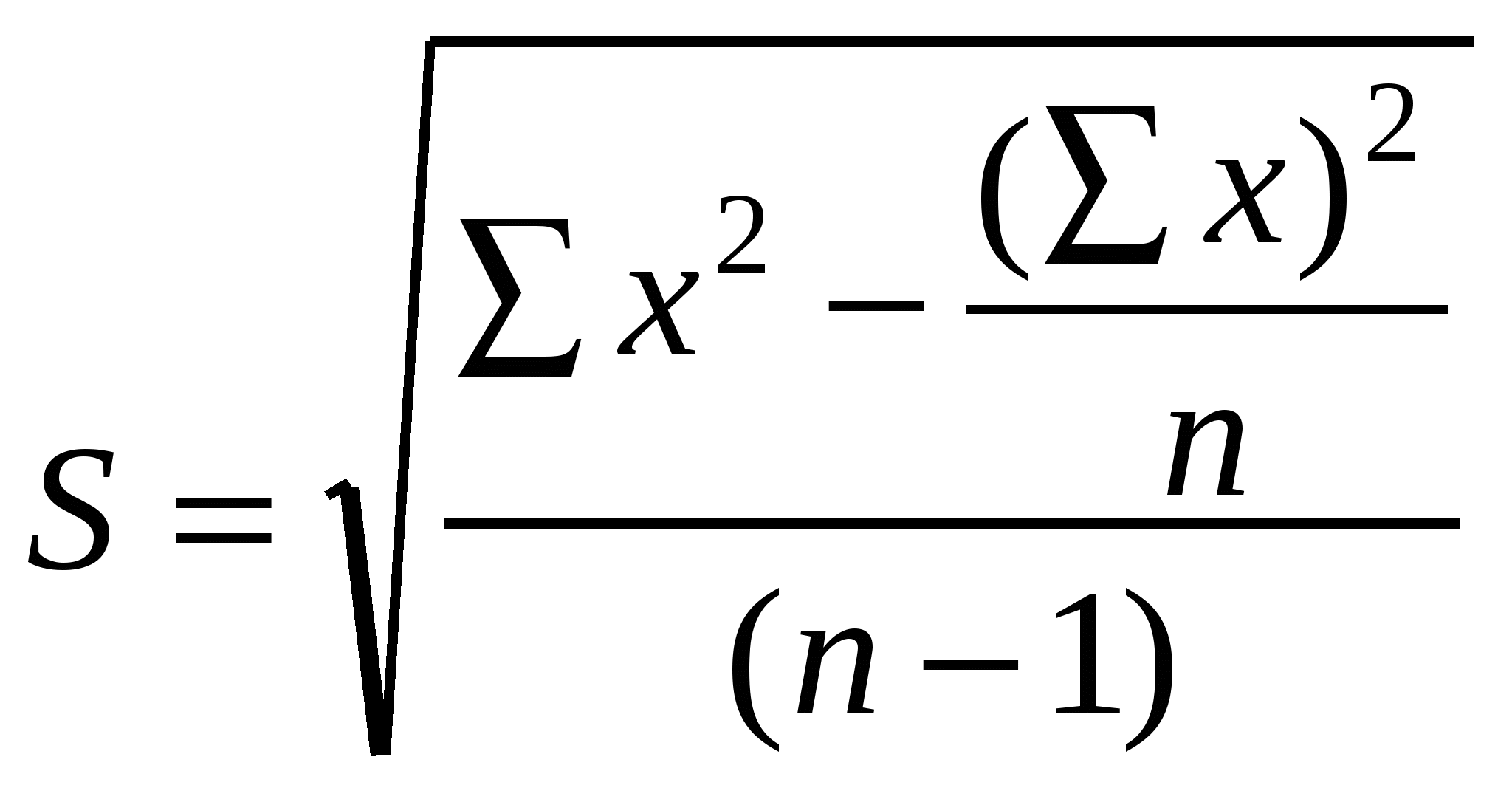

,

где Σ x² – сумма квадратов значений признака для всех вариант,

Σ x –сумма значений признака,

n – объем вы­борки.

Для примера с массой тела бурозубок стандартное отклонение будет равно: S = 0.897216496, а после необходимого округления S = 0.897 г.

В некоторых случаях бывает необходимо определить взвешенное сред­нее квадратичное отклонение для суммарного распределения, составленного из нескольких выборок, для которых значения стандартных отклонений уже известны. Эта задача решается с помощью формулы: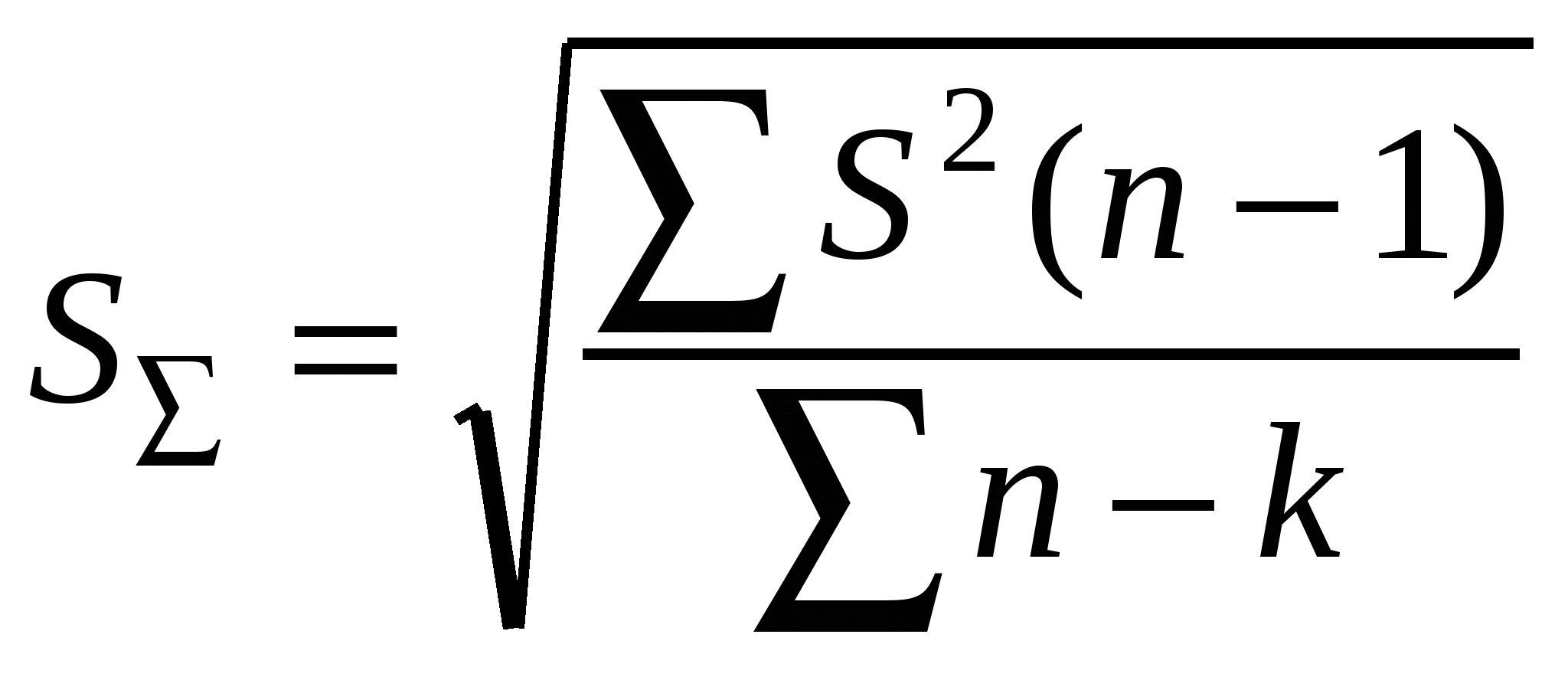

,

где S_Σ – усредненная величина среднего квадратичного откло­нения для суммарного распределения,

S ­­– усредняемые значе­ния стандартного отклонения,

п–объемы отдельных выборок,

k – число усредняе­мых стандартных отклонений.

Рассмотрим такой пример. Четыре независимых определе­ния веса печени (мг) у землероек-бурозубок в июне, июле, ав­густе и сентябре дали следующие величины стандартных отклонений: 93, 83, 50, 71 (при n = 17, 115, 132, 140). Подставив в вышеприведенную фор­мулу нужные значения, получим стандартные отклонения для суммарной выбор­ки (для всего бесснежного периода):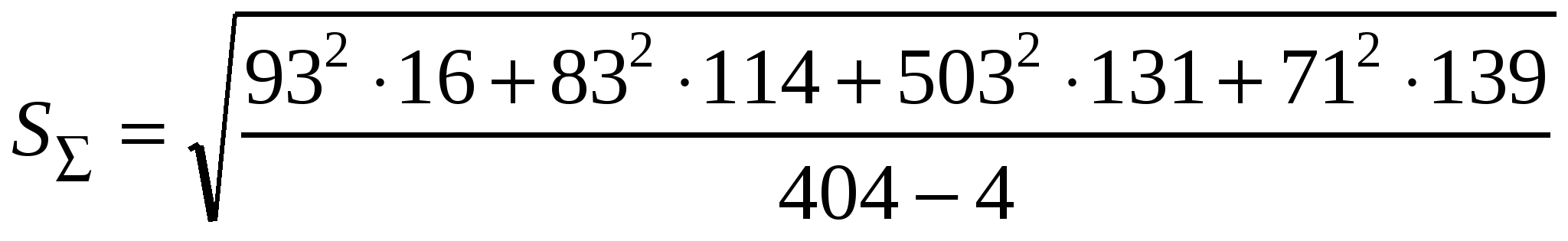

= 69.9.

В случае, если требуется первичная статистическая обработка большого числа выборок, но необязательно с большой точностью, для оценки стандартного отклонения можно воспользоваться экспресс-методом, основанным на знании закона нормального распределения. Как уже отмечалось, крайние значения для выборки (с вероятностью P = 95%) можно считать границами, удаленными от средней на расстояние 2S: x_min = M − 2S, x_max = M + 2S. Это значит, что в лимите (Lim), в диапазоне от максимального до минимального выборочного значения, укладываются четыре стандартных отклонения:

Lim = (M + 2S) − (M − 2S) = 4S.

Однако этот вывод справедлив только по отношению к выборкам большого размера, тогда как для небольших выборок необходимо делать поправки. Рекомендуется следующая формула приблизительного расчета стандартного отклонения (Ашмарин и др., 1975):

,

где величина d взята из таблицы 3 (против соответствую­щего объема выборки, n).
Таблица 3

п	d	п	d	п	d	n	d
2	1.128	7	2.704	12	3.258	17	3.588
3	1.693	8	2.847	13	3.336	18	3.640
4	2.059	9	2.970	14	3.407	19	3.689
5	2.326	10	3.079	15	3.472	20	3.735
6	2.534	11	3.173	16	3.532	более	4

Выборочное стандартное отклонение веса тела бурозубок (n = 63), рассчитанное по приведенной формуле, составляет:

S= (11.9 − 7.3) / 4 = 1.15 г,

что достаточно близко к точному значению, S = 0.89 г.

Использование экспресс-оценок стандартного отклонения значительно сокращает время расчетов, существенно не сказываясь на их точности. Отмечается лишь небольшая тенденция к завышению получаемых этим методом значений стандартного отклонения при небольших объемах выборок.

Стандартное отклонение – величина именованная, поэтому с ее помощью можно сравнивать характер варьирования лишь одних и тех же признаков. Чтобы сопоставить изменчивость разнородных признаков, выраженных в различных единицах измерения, а также нивелировать влияние мас­штаба измерений, используют так называемый коэффициент вариации (СV), безразмерную величину, отношение выборочной оценки S к собственной средней M:

.

В нашем примере с весом тела бурозубок:

 9.6%.

Индивидуальная изменчивость (варьирование) признаков – одна из наиболее емких характеристик биологи­ческой популяции, любого биологического процесса или явле­ния. Коэффициент вариации может считаться вполне адекватным и объективным показателем, хорошо отражающим фактическое разнообразие совокупности независимо от абсолютной величины признака. Индекс был создан для унификации показа­телей изменчивости разных или разноразмерных признаков пу­тем приведения их к одному масштабу. Практика показывает, что для многих биологических признаков наблюдается увеличение изменчивости (стандартного отклонения) с ростом их величины (средней арифметической). При этом коэффициент вариации остается примерно на одном и том же уровне – 8–15%. За увеличение коэффициента вариации ответственны, как правило, растущие отличия распределения признака от нормального закона.