Элементарная биометрия. Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях

• Название: Книга служит элементарным пособием для практического применения вариационной статистики в биологических исследованиях
• Анкор: Элементарная биометрия.doc
• Дата: 04.01.2018
• Размер: 3.04 Mb.
• Имя файла: Элементарная биометрия.doc
• Тип: Книга; #13667
• страница: 17 из 32

Множественная корреляция

Разобранные выше примеры корреляционных зависимостей касались главным образом взаимосвязи двух сопряженных про­цессов, явлений или варьирующих признаков. Между тем в практике биологических исследований нередко приходится сталкиваться с более сложными случаями, например, когда со­пряжены не два, а три или более изменчивых фактора (призна­ка). В такой ситуации возникает необходимость изучить множественные связи между большим числом взаимодействующих переменных, выступающих как в виде целой системы коррелированных признаков организма, так и в форме совместного влияния сложной совокупности факторов на определенное явление. Корреляционная зависимость нескольких переменных носит название множествен­ной корреляции и оценивается коэффициентом, определяемым на основе корреляций между всеми парами признаков. Например, коэффициент множественной корреляции между тремя признаками А, В и С вычисляется по фор­муле: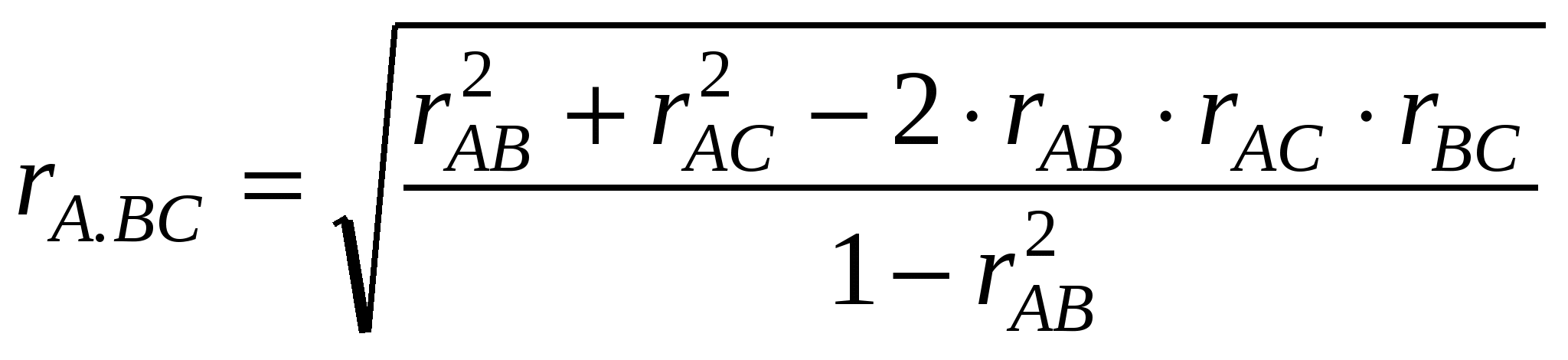

.

Полученная величина характери­зует связь первого признака (A) с двумя другими (B и C). Покажем этот способ на примере совокупного действия двух факторов, В и С (температуры и влажности), на суточную ак­тивность травяных лягушек (A). Опреде­ление парных корреляций дало следующие результаты (n = 110): r_АB= +0.58; r_АC= +0.80; r_BC = −0.45. Отсюда

 = 0.86.

Сводный коэффициент корреляции оказался довольно высоким и, как показывает его сопоставление со стандартным значением по таблице 15П, вполне достоверным (при α < 0.001).

С другой стороны, если обнаружена значительная корреля­ция между признаками A и С и между В и С, то не исключена возможность мнимой корреляционной зависимости между A и В,которая создается за счет одновременного влияния на них тре­тьего признака С. Например, установленная по ис­следованиям в Карелии корреляция между численностью лес­ных полевок и урожаем семян сосны, скорее всего, объясняется не значением последних в питании грызунов (т. е. прямой при­чинной связью), а тем, что оба эти явления (численность поле­вок и урожай семян) контролируются одними и теми же эколо­гическими факторами (прежде всего метеорологическими) и по­этому изменяются параллельно, хотя непосредственно между собой не связаны.

В этом и подобных случаях (например, когда настоящие за­висимости между признаками животных маскируются влиянием возраста или когда связи между отдельными промерами орга­низма создаются за счет влияния живого веса и т. д.) возника­ет задача изучить корреляцию между двумя признаками (A и В), исключив влияние на эту связь третьего признака (С), как бы элиминировав его.

Частная корреляция

Этой цели служит коэффициент частной корреляции, оцени­вающий связь между первым и вторым признаками при посто­янных значениях третьего и вычисляемый по формуле:

,

где A и В – факторы, связь которых требуется изучить;

С – фактор, влияние которого необходимо исключить из корреля­ционной зависимости между A и В (реперный признак);

r_АB, r_АС, r_BС – соответст­вующие парные коэффициенты корреляции, вычисляемые обыч­ным способом;

r_А(BС) – искомый коэффициент частной корреляции, по­казывающий связь между двумя признаками при исключении влияния третьего.

Этот же метод можно применить и для элиминации двух факторов при четырех переменных и т. д. Формула для расчетов примет в этом случае следующий вид: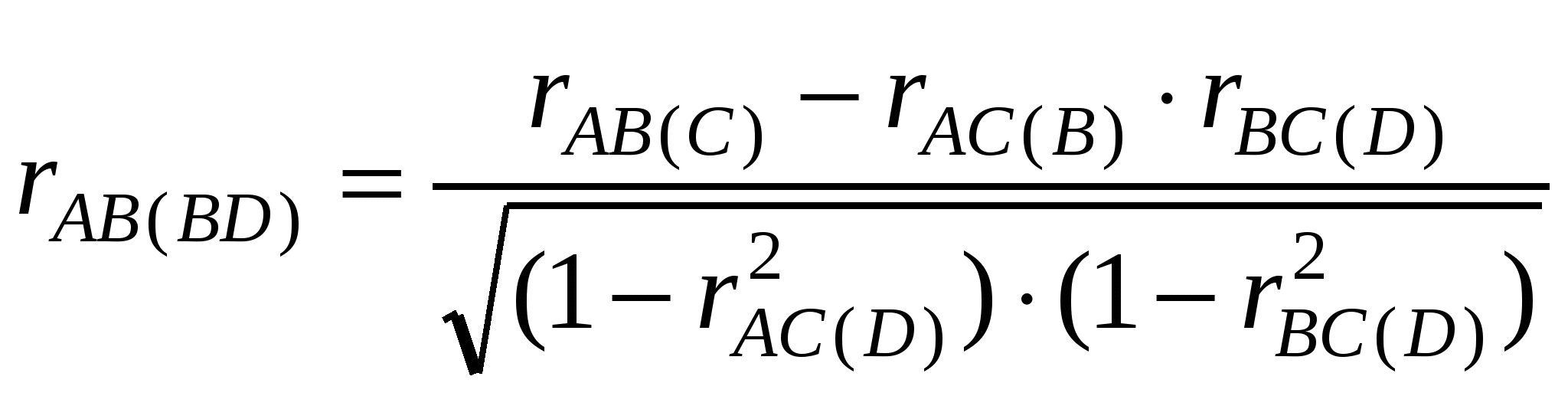

.

Рассмотрим нахождение коэффициента частной корреляции на упрощенном примере (взятом из книги П. Ф. Рокицкого). Получены данные о корреляции между давлением крови (A), содержанием в ней холестерина (В) и возрастом (С) у 142 женщин. Соответствующие коэффициенты корреляции таковы: r_АB= +0.25; r_АC= +0.33; r_BC= 0.51.

Известно, что повышенное артериальное давление может быть связано с высоким содержанием холестерина в стенках кровеносных сосудов, однако и давление крови, и концентрации холестерина увеличиваются с возрастом. Поэтому возникает вопрос, создается ли корреляция между давлением крови и со­держанием в ней холестерина за счет их общей связи с возрас­том или же она реально существует для каждого возраста (и независимо от него). Элиминируя эффект возраста по приве­денной выше формуле, получим:

= 0.12.

По таблице 15П можно установить, что при п = 150 для достоверности коэффициента корреляции даже при уровне значимости α = 0.05 его величина должна быть не меньше 0.159. В данном же случае полученное значение меньше табличного и, следовательно, коэффициент корреляции от нуля достоверно не отличается. Таким образом, внутри отдельных возрастных групп корреляционной связи между дав­лением крови и содержанием холестерина, по крайней мере на изученном материале, не обнаруживается. Пока нет оснований отбрасывать нулевую гипотезу.

Второй пример демонстрирует использование коэффициента частной корреляции для более глубокого проникновения в структуру нескольких факторов наведения. Рассмотрим выборку объектов разного статуса (11 видов мелких млекопитающих), взяв в качестве признаков их численность в семи биотопах прибайкальской равнины. Реперным признаком послужила суммарная численность вида во всех биотопах. Здесь коэффициент корреляции отражает сходство между биотопами по соотношениям численности 11 видов. Например, оказалось, что между березняком и экотоном (граница между березняком и коренными лесами) и общая корреляция (r= 0.92), и частная (r= 0.64) высока и положительна. Можно утверждать, что население животных этих биотопов почти идентично.

В свою очередь, корреляция между кедровником и лугом не проявилась (r= −0.08), но коэффициент частной корреляции был велик и отрицателен (r= −0.43). Этим оттеняется тот факт, что виды, отсутствующие на лугу, многочисленны в кедровнике (красная полевка, мышь), а обычные в агроценозе – крайне редки в тайге (серые полевки).

Частная корреляция показала, что население этих биотопов во многом диаметрально противоположно. Она выявила два вида факторов наведения. Один из них хорошо известен – это сезонное расселение видов в другие биотопы. В течение периода размножения видовой состав тайги и луга меняется несогласованно (одни виды идут из тайги в агроценозы, другие – в противоположном направлении) и численность всех видов относительно выравнивается, r= −0.08. Частная корреляция устраняет эффект прироста численности за счет иммигрантов и выдвигает на первый план контраст «базовой» численности, которую формируют характерные обитатели биотопов: в тайге это лесные полевки, на лугу – серые. Так проявляется второй фактор: отличие качества среды в разных биотопах. Он обеспечивает формирование принципиально несходных зооценозов, что и показывает высокой частной корреляцией r= −0.43.