лекцииММиИТпП-ч.1. Конспект лекций ч. 1 Омск

• Название: Конспект лекций ч. 1 Омск
• Дата: 15.11.2021
• Размер: 1.27 Mb.
• Имя файла: лекцииММиИТпП-ч.1.docx
• Тип: Конспект; #273057
• страница: 13 из 16

4. Моделирование в условиях неопределенности

Развитие современных технологий во всех сферах деятельности человека и разработка соответствующих моделей приводят к необходимости учета максимально возможного количества информации об исследуемом объекте. При этом вопросы моделирования сложных процессов и явлений чаще всего формулируются и обсуждаются на профессиональном языке (искусственном или подмножестве естественного), отражающем специфику области исследования. Следствием этого является использование в процессе моделирования качественных элементов: описаний, понятий и отношений с неопределенными или нечеткими границами, высказываний с многозначной шкалой истинности и т.д.

В тех случаях, когда информация существенно неопределенная, задание строгих границ «волевым» порядком или искусственное введение однозначности означает не что иное, как огрубление исходных данных, и может приводить к получению пусть четкого, но неверного результата. Исследование и учет однозначности (определенности) или неоднозначности (неопределенности) всех параметров и отношений, описывающих исследуемое явление, представляет собой необходимый и важнейший элемент математического моделирования.

Известные закономерности, описывающие процессы и явления объективного мира, можно условно разделить на две группы: однозначно определенные (детерминированные) и находящиеся в условиях неопределенности.

К первой группе относят те закономерности, которые по заданным с определенной точностью характеристикам воздействий позволяют установить вполне определенный (детерминированный) отклик (реакцию) исследуемого объекта. Например, материальное тело падает с некоторой высоты. При заданной точности определения начальных условий и действующих на тело внешних сил можно однозначно, с определенной точностью установить его скорость при соприкосновении с Землей, время полета и т.д. С математической точки зрения эти закономерности описываются на основе аксиом традиционной математикой с использованием вполне определенных величин.

Вторая группа закономерностей описывает случайные события (такие, которые при заданном комплексе условий могут протекать по-разному при одних и тех же условиях). Например, при бросании игрального кубика нельзя заранее однозначно сказать, какая цифра выпадет. Если попытаться учесть природу этих закономерностей как явлений, находящихся в условиях неопределенности, то надо иметь в виду, что описание этой неопределенности может быть разным в зависимости от количества и качества имеющейся информации.

Часто граница, отделяющая случайное событие от неслучайного, очень размытая. Одна из концепций случайности (которая преобладала до начала XX столетия) состояла в том, что если при описании исследуемого объекта предусмотреть все связанные с ним «детали», то никакой случайности не будет. Однако в настоящее время принято придерживаться другой концепции. Вернемся к примеру с падением материального тела. При полете последнего необходимо учитывать температуру окружающей среды, скорость ветра, положение относительно поверхности Земли и другие факторы, которые имеют неоднозначный характер и могут, в свою очередь, влиять друг на друга. Поэтому в «чистом виде» однозначно определенных процессов (явлений), наверное, нет, т.е. при описании достаточно сложных процессов закономерности всегда носят стохастический характер.

4.1. Причины появления неопределенностей и их виды

При решении задач математического моделирования (задачи проектирования, описания различных технологических процессов, выбора оптимальных параметров и т.д.) уже на стадии концептуальной постановки необходимо задуматься над тем, насколько однозначно определены параметры, в терминах которых осуществляется математическое описание объекта моделирования. На этом этапе необходимо определить для каждого параметра, можно ли считать его однозначно определенным или ему присуща некоторая неопределенность. Причем неопределенными могут быть не только параметры, но и связи между ними. Неопределенность понимается в том смысле, что соответствующие характеристики рассматриваемой системы находятся в условиях приближения и неполноты информации. Эта неопределенность может быть связана, с одной стороны, с тем, что параметры могут изменяться случайным образом, а с другой стороны, с тем, что они могут адаптироваться (изменяться, устанавливаться) в процессе функционирования исследуемой системы.

К наиболее значимым причинам появления неопределенности можно отнести следующие:

показатели системы практически всегда зависят от большого количества различных факторов, причем часть из них может быть даже неизвестна исследователю;

при построении модели обычно ограничиваются отбором наиболее существенных (по мнению субъекта или в силу объективных обстоятельств) переменных, что, конечно, приводит к огрублению модели;

математические погрешности, возникающие при линеаризации модели или использовании разложения в ряд при ограничении на число членов ряда; ошибки измерений и по грешности при проведении эксперимента и т.п.

В общем случае все причины возникновения неопределенности можно разбить на две основные группы: субъективные и объективные. Субъективные причины обусловлены некоторыми частными, нерегулярно повторяющимися явлениями, поэтому их достаточно сложно учесть при решении прикладных задач. Объективные причины чаще всего связаны с физическими особенностями исследуемого явления.

Например, если рассматривать задачу исследования некоторого технологического процесса, то к субъективным причинам можно отнести квалификацию работников, проводящих и регламентирующих исследуемый процесс, их навыки, реакцию, время адаптации и т.д. К объективным причинам появления неопределенности для такого типа задач можно отнести:

физико-механические свойства поставляемых материалов (в частности, предел текучести, модуль Юнга, коэффициенты теплопроводности, теплоемкости, теплоотдачи и т.д.);

анизотропию свойств;

поля остаточных напряжений;

геометрические характеристики заготовок (форма и размеры);

характер износа инструмента и т.д.

В свою очередь каждая из указанных объективных причин появления неопределенности может быть обусловлена целым рядом предпосылок. Так, неоднородность свойств материала, с одной стороны, определяется как неоднородность по объему, обусловленная особенностями технологического процесса (отливки, прокат, армированные и порошковые композиты и прочие), а с другой – как неоднородность партий поставляемых заготовок. При решении прикладных задач для устранения неопределенностей обычно вводится предположение о принятии в качестве физико-механических характеристик некоторых предельных или средних значений (из возможных диапазонов). На наш взгляд, подобное предположение является весьма спорным в силу нелинейности исследуемых процессов и сложного характера взаимодействия отдельных частей объекта между собой. Поэтому возникает необходимость учета распределения соответствующей неопределенной величины.

В зависимости от полноты описания неопределенность можно разбить на три основные группы: неизвестность, недостоверность и неоднозначность. Рассмотрим группы описания неопределенности более подробно (рис. 4.1).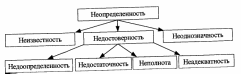

Рис. 4.1. Виды описания неопределенности
Неизвестность – это начальная стадия описания неопределенности, при которой информация полностью отсутствует.

Недостоверность – это вторая стадия описания неопределенности, которая для различных стадий сбора информации может

классифицироваться как неполнота, недостаточность, недоопреде-ленность и неадекватность. Неполнота характеризуется тем, что собрана не вся возможная информация; недостаточность – собрана не вся необходимая информация. Недоопределенность – для некоторых элементов определены не их точные описания, а лишь множества, которым эти описания принадлежат; неадекватность – ряд элементов исследуемого объекта описан по аналогии с уже имеющимися описаниями подобных элементов, т.е. имеет место так называемое «замещающее» описание, которое не всегда удовлетворяет целям исследования.

Дальнейший анализ неопределенности, учет новых факторов, определяющих исследуемое явление, может привести либо к устранению неопределенности (все элементы описаны однозначно), либо к неоднозначности.

Неоднозначность – это конечная (по полноте возможного описания) степень неопределенности, когда вся возможная информация собрана, но полностью необходимое описание не получилось. Причины возникновения неоднозначности могут быть лингвистические и физические (рис. 4.2).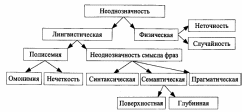


Рис. 4.2. Причины возникновения неоднозначности
Физическая неопределенность связана либо с наличием нескольких возможностей, каждая из которых случайным образом может стать реальностью, либо с неточностью вычислений или измерений. Таким образом, физическая неопределенность связана или с физической сущностью исследуемого явления, или с его измеряемыми проявлениями.

Лингвистическая неопределенность связана с использованием некоторого естественного языка. Она порождается, с одной стороны, множественностью значений слов (понятий и отношений) – полисемией (греч. – многозначность), с другой – неоднозначностью смысла фраз.

Можно выделить два вида полисемии: омонимию и нечеткость.

Омонимия (греч. одноименность) характеризуется тем, что одним и тем же словом можно характеризовать различные физические объекты. Например: коса – это вид побережья, инструмент или прическа. Если же объекты описания сходны по сути, но описывают некоторое множество понятий, то ситуацию относят к нечеткости. Например, понятие несколько шагов. Это может быть два шага, три шага, четыре шага и т. д.

Рассматривая источники неоднозначности смысла фраз, можно выделить синтаксическую, семантическую и прагматическую неоднозначность. При синтаксической неопределенности уточнение синтаксиса позволяет понять смысл фразы. Пример: «казнить нельзя помиловать» – «казнить, нельзя помиловать» или «казнить нельзя, помиловать». Семантическая неопределенность бывает поверхностная и глубинная. В первом случае отдельные слова понятны, но неясен смысл фразы («голубые зеленые мысли яростно спят»), во втором случае непонятны и все отдельные слова («глокая куздра штеко будланула бокра и курдячит бокренка»). Прагматическая неопределенность связана с совместным проявлением синтаксической и семантической неопределенностей. Она чаще всего проявляется при работе с незнакомыми объектами и, возможно, в незнакомой (например, языковой) среде.

Как уже отмечалось, на стадии концептуальной постановки задачи необходим детальный анализ степени неопределенности всех характеристик системы и связей между ними. При переходе к математической постановке задачи перед исследователем встают непростые вопросы: каким типом переменных описать те или иные параметры и как описать связь между этими параметрами?

Если цели исследования предполагают однозначное описание явления (процесса) или если параметры системы и связи между ними определены единственно возможным образом, то в этом случае применяется четкое описание, т.е. все характеристики считаются детерминированными и связи между соответствующими четкими переменными – однозначными. В противном случае в зависимости от целей исследования и требуемой полноты описания можно использовать различные математические подходы представления неопределенностей. Отметим, что усложнение модели (например, иерархичность) также может привести к необходимости использования других типов описания переменных, характеризующих исследуемое явление.

Математически неопределенность может быть описана стохастически, статистически, с позиций теории нечетких множеств, а также интервально (рис. 4.3). Отмеченные формы описания перечислены по возрастанию степени неопределенности. Рассмотрим физический смысл этих неопределенностей.


Рис. 4.3. Формы описания неопределенности
Стохастическое описание используется тогда, когда неопределенные параметры имеют вероятностный (случайный) характер.

При этом необходимо, чтобы был определен закон распределения таких случайных параметров. Стохастическим описанием занимается теория вероятностей и теория случайных процессов.

Статистическое описание является, по существу, частным случаем стохастического описания. Эту форму описания применяют, когда заданы только выборочные оценки каких-либо характеристик случайной величины или наборы значений некоторых случайных параметров. Статистическим описанием занимается математическая статистика.

При описании с позиций нечетких множеств неопределенный параметр задается некоторым множеством возможных его значений, характеризующихся той или иной степенью принадлежности (с помощью так называемой функции принадлежности) объекту, описываемому этим нечетким множеством. Функция принадлежности может принимать значения от 1 (полная принадлежность) до 0 (полная непринадлежность). Интерпретацией функции принадлежности является субъективная мера того, насколько полно элемент (параметр) соответствует понятию, смысл которого описывается нечетким множеством. Этим описанием занимается теория нечетких множеств.

Интервальное описание можно использовать, когда неопределенные параметры заданы только диапазонами возможных значений (верхней и нижней границами), причем параметр может принимать любое значение внутри интервала и ему нельзя приписать никакой вероятностной меры. Интервальное описание является предметом исследования интервальной математики.

Следует отметить, что зависимость математического подхода к описанию переменных от полноты имеющейся информации весьма условна. Так, при численной реализации тех или иных алгоритмов моделей на ЭВМ даже для детерминированных переменных (неявным образом) используется аппарат интервальных вычислений, так как расчеты на ЭВМ ведутся с интервальными величинами. Поэтому считать, что интервальное описание переменных «менее определенное», чем стохастическое, наверное, нельзя. Однако с этим утверждением можно согласиться, если интервальное описание вводится уже на стадии концептуальной и математической постановок задач.

Многообразие форм описания неопределенностей приводит к различным особенностям постановки и решения соответствующих задач.

4.2. Вопросы для самопроверки

Сформулируйте основные причины появления неопределенностей. Какие из них являются субъективными, а какие – объективными?

Как различается неопределенность в зависимости от полноты и качества описания?

Какие основные причины возникновения неоднозначности вы знаете?

Приведите примеры лингвистических и физических неоднозначностей.

Как описывается неопределенность математически?

Приведите примеры математического описания неопределенностей для различных физических явлений.