лекцииММиИТпП-ч.1. Конспект лекций ч. 1 Омск

• Название: Конспект лекций ч. 1 Омск
• Дата: 15.11.2021
• Размер: 1.27 Mb.
• Имя файла: лекцииММиИТпП-ч.1.docx
• Тип: Конспект; #273057
• страница: 11 из 16

2.5. Этапы построения математической модели

Процесс создания математических моделей трудоемок, длителен и связан с использованием труда различных специалистов достаточно высокого уровня, обладающих хорошей подготовкой как в предметной области, связанной с объектом моделирования, так и в области прикладной математики, современных численных методов, программирования, знающих возможности и особенности современной вычислительной техники. Отличительной особенностьюматематических моделей, создаваемых в настоящее время, является их комплексность, связанная со сложностью моделируемых объектов. Например, при моделировании процессов деформирования различных конструкций под действием приложенной нагрузки приходится учитывать не только происходящие при деформировании процессы массопереноса, но и теплоперенос, а также связанные с этими процессами изменения структуры и свойств материала.

В некоторых случаях необходимо учитывать влияние различных видов излучения, воздействия гравитационных и электромагнитных полей, предыстории деформирования. Кроме того, для современных моделей характерно представление объекта моделирования в виде более или менее сложной системы взаимодействующих элементов.

Все отмеченные выше особенности приводят к усложнению модели и необходимости совместного использования нескольких теорий (нередко – из разных областей знания), применения современных вычислительных методов и вычислительной техники для получения и анализа результатов моделирования.

Внедрение вычислительной техники во все сферы человеческой деятельности привело к повсеместному использованию математических моделей. Заметим, что ЭВМ - это только «железо», а «умным» и полезным его делают программы, которые в большинстве случаев являются реализациями алгоритмов соответствующих математических моделей. Поэтому необходимо создание большого количества разнообразных математических моделей с широкими возможностями, отвечающих различным, зачастую противоречивым, требованиям. В случае сложных объектов удовлетворить всем предъявляемым требованиям в одной модели обычно невозможно. Приходится создавать целый спектр моделей одного и того же объекта (в некоторых случаях - иерархическую совокупность «вложенных» одна в другую моделей), каждая из которых наиболее эффективно решает возложенные на нее задачи. Например, в конструкторской и технологической практике, как правило, применяется широкий спектр моделей – от простых расчетных формул (часть, из которых представляет собой аппроксимацию экспериментальных данных) на первоначальной стадии до весьма сложных моделей, приближающихся к исследовательским, - на завершающей стадии разработки конструкции или технологического процесса.

Модели, ориентированные на исследовательские цели, способны представлять объект в широком диапазоне исходных параметров с удовлетворительной точностью. При этом практически нет ограничений по сложности подобной модели, а также времени, затрачиваемом на получение результатов.

Исследовательские модели могут быть ориентированы как на количественные, так и на качественные результаты. К моделям, используемым в автоматизированных системах управления (АСУ), в отличие от исследовательских, предъявляются достаточно жесткие ограничения относительно времени, затрачиваемого на получение результатов, а также точности самих результатов.

Необходимость массового построения моделей требует разработки некоторой совокупности правил и подходов, которые позволили бы снизить затраты на разработку моделей и уменьшить вероятность появления трудно устранимых впоследствии ошибок. Подобную совокупность правил можно было бы назвать технологией создания математических моделей.

Процесс построения любой математической модели можно представить последовательностью этапов, представленных на рис. 2.1.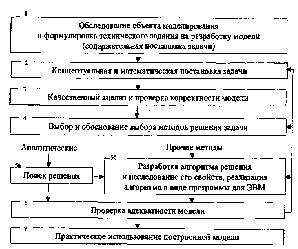


Рис. 2.1. Этапы построения математической модели

2.5.1. Обследование объекта моделирования

Математические модели, особенно использующие численные методы и вычислительную технику, требуют для своего построения значительных интеллектуальных, финансовых и временных затрат. Поэтому решение о разработке новой модели принимается лишь в случае отсутствия иных, более простых путей решения возникших проблем (например, модификации одной из существующих моделей). Необходимость в новой модели может появиться в связи с проведением научных исследований (особенно – на стыке различных областей знания), выполнением проектных и конструкторских работ на производстве, созданием систем автоматического управления, планирования и контроля. Человека или организацию, заинтересованных в разработке новой математической модели, для краткости будем называть заказчиком. После принятия решения о необходимости построения новой математической модели заказчик ищет исполнителя своего заказа. В качестве исполнителя, как правило, может выступать рабочая группа, включающая специалистов разного профиля: прикладных математиков, специалистов, хорошо знающих особенности объекта моделирования, программистов.

Итак, если решение о создании модели принято и рабочая группа сформирована, то можно приступать к этапу обследования объекта моделирования. Основной целью данного этапа является подготовка содержательной постановки задачи моделирования.

Перечень сформулированных в содержательной (словесной) форме основных вопросов об объекте моделирования, интересующих заказчика, составляет содержательную постановку задачи моделирования.

Подготовка списка вопросов, на которые должна ответить новая модель, зачастую является самостоятельной проблемой, требующей для своего решения специалистов со специфическими знаниями и способностями. Они должны не только хорошо разбираться в предметной области моделирования, знать возможности современной вычислительной математики и техники, но и быть достаточно коммуникабельными, т.е. уметь общаться с людьми, «разговорить» практиков, хорошо «чувствующих» объект моделирования, нюансы его поведения. Подобных специалистов в настоящее время называют постановщиками задач.

На основании анализа всей собранной информации постановщик задачи должен сформулировать такие требования к будущей модели, которые, с одной стороны, удовлетворяли бы заказчика, а с другой – позволяли бы реализовать модель в заданные сроки и в рамках выделенных материальных средств.

Специалисты-постановщики должны обладать способностью из большого объема слабо формализованной разнообразной информации об объекте моделирования, из различных нечетко высказанных и сформулированных пожеланий и требований заказчика к будущей модели выделить то главное, что может быть действительно реализовано. Из перечисленных требований, предъявляемых к постановщикам задач, видно, насколько велика возложенная на них ответственность и насколько могут быть тяжелы допущенные ими ошибки и просчеты. Неправильная оценка срока и стоимости реализации требуемой модели может привести к неудаче всего проекта, к напрасной потере времени и средств.

Специалисты, предрасположенные к работе в качестве постановщиков задач, особенно ценятся и являются, без преувеличения, золотым фондом научных коллективов. По этому поводу Г.Биркгоф отмечает, что прикладники-математики, «способные к глубокому общению с другими учеными и инженерами и знакомые с мощью и ограничениями цифровых машин, ... призваны стать вождями завтрашнего математического мира, но их будет крайне трудно найти и развить». С учетом данного высказывания, а также имея в виду конечную цель деятельности рабочей группы – построение математической модели, - представляется целесообразным рекомендовать в качестве руководителя группы именно прикладника-математика.

Этап обследования проводится членами рабочей группы под руководством постановщиков задач и включает следующие работы:

тщательное обследование собственно объекта моделирования с целью выявления основных факторов, механизмов, влияющих на его поведение, определения соответствующих параметров, позволяющих описывать моделируемый объект;

сбор и проверка имеющихся экспериментальных данных об объектах-аналогах, проведение при необходимости дополни тельных экспериментов;

аналитический обзор литературных источников, анализ и сравнение между собой построенных ранее моделей данного объекта (или подобных рассматриваемому объекту);

анализ и обобщение всего накопленного материала, разработка общего плана создания математической модели.

На основе собранной информации об объекте моделирования постановщики совместно с заказчиком формулируют содержательную постановку задачи моделирования, которая, как правило, не бывает окончательной и может уточняться и конкретизироваться в процессе разработки модели. Однако, с учетом изложенного выше, все последующие уточнения и изменения содержательной постановки должны носить частный, не принципиальный характер. Если объектом моделирования является технологический процесс, машина, конструкция или деталь, то содержательную постановку задачи моделирования очень часто называют технической постановкой задачи.

Весь собранный в результате обследования материал о накопленных к данному моменту знаниях об объекте, содержательная постановка задачи моделирования, дополнительные требования к реализации модели и представлению результатов оформляются в виде технического задания на проектирование и разработку модели.

Техническое задание является итоговым документом, заканчивающим этап обследования, который, как уже отмечалось, является очень важным и ответственным. Чем более полную информацию удастся собрать об объекте на этапе обследования, тем более четко можно выполнить содержательную постановку задачи, более полно учесть накопленный опыт и знания, избежать многих сложностей на последующих этапах разработки модели. Особенно строго необходимо формулировать требования к будущей модели. Неконкретные и нечеткие требования могут серьезно затруднить процесс сдачи модели заказчику, вызвать бесконечные доработки и улучшения. В целом этап проработки технического задания может составлять до 30% времени, отпущенного на создание всей модели, и даже более – с учетом возможного уточнения и переформулировки.

Понимая огромную важность рассматриваемого этапа, техническое задание следует подвергать внутренней (внутри организации) и внешней экспертизе независимыми экспертами, не участвующими в его разработке. Обязательным условием на этапе разработки технического задания является участие в его обсуждении всех членов рабочей группы.

2.5.2. Концептуальная постановка задачи моделирования

В отличие от содержательной концептуальная постановка задачи моделирования, как правило, формулируется членами рабочей группы без привлечения представителей заказчика, на основании разработанного на предыдущем этапе технического задания, с использованием имеющихся знаний об объекте моделирования и требований к будущей модели.

Анализ и совместное обсуждение членами рабочей группы всей имеющейся информации об объекте моделирования позволяет сформировать содержательную модель объекта, являющуюся синтезом когнитивных моделей, сложившихся у каждого из членов рабочей группы. На основании содержательной модели разрабатывается концептуальная, или «естественнонаучная» (физическая, химическая, биологическая и т.д.), постановка задачи моделирования, служащая основой для концептуальной модели объекта.

Концептуальная постановка задачи моделирования – это сформулированный в терминах конкретных дисциплин (физики, химии, биологии и т.д.) перечень основных вопросов, интересующих заказчика, а также совокупность гипотез относительно свойств и поведения объекта моделирования.

Наибольшие трудности при формулировке концептуальной постановки приходится преодолевать в моделях, находящихся на «стыке» различных дисциплин. Различия традиций, понятий и языков, используемых для описания одних и тех же объектов, являются очень серьезными препятствиями, возникающими при создании «междисциплинарных» моделей. Например, такие понятия как «прибыль» и «баланс» вызывают совершенно разные ассоциации у экономиста и математика-прикладника.

Можно сказать, что когнитивные модели, стоящие за этими понятиями, у этих двух специалистов совершенно различны. Если экономист, говоря о прибыли и балансе, связывает с этими понятиями конкретное производство, цену и себестоимость продукции, то для математика данные понятия выглядят более формально – как результаты решения некоторых математических уравнений. При этом практически невозможно научить математика мыслить как экономиста, а экономиста – как математика. И тот, и другой способ восприятия имеет свои достоинства и недостатки. Экономист никогда не сделает ошибок, которые может допустить математик, обращаясь с параметрами модели формально, без должных знаний в рассматриваемой предметной области. В то же время, используя формальные преобразования математических соотношений, математик может получить решения, которые очень сложно получить экономисту, пользующемуся своими подходами и методами (обычно более простыми с точки зрения математики). Поэтому эффективность деятельности рабочей группы в большой степени зависит от способности ее членов поставить себя на место специалиста другого профиля, изучить его точку зрения (т.е. особенности его когнитивной модели) и найти некоторый компромисс, учитывающий все ценное.

Выше отмечалось, что концептуальная модель строится как некоторая идеализированная модель объекта, записанная в терминах конкретных (например, естественнонаучных) дисциплин. Для этого формулируется совокупность гипотез о поведении объекта, его взаимодействии с окружающей средой, изменении внутренних параметров. Как правило, эти гипотезы правдоподобны в том смысле, что для их обоснования могут быть приведены некоторые теоретические доводы и использованы экспериментальные данные, основанные на собранной ранее информации об объекте. В выборе и обосновании принимаемых гипотез в значительной степени проявляется искусство, опыт и знания, накопленные членами рабочей группы. Согласно принятым гипотезам определяется множество параметров, описывающих состояние объекта, а также перечень законов, управляющих изменением и взаимосвязью этих параметров между собой.

2.5.3. Математическая постановка задачи моделирования

Законченная концептуальная постановка позволяет сформулировать математическую постановку задачи моделирования, включающую совокупность различных математических соотношений, описывающих поведение и свойства объекта моделирования.

Математическая постановка задачи моделирования – это совокупность математических соотношений, описывающих поведение и свойства объекта моделирования.

Как было отмечено выше, совокупность математических соотношений определяет вид оператора модели. Наиболее простым будет оператор модели в случае, если он представлен системой алгебраических уравнений. Подобные модели можно назвать моделями аппроксимационного типа, так как для их получения часто используют различные методы аппроксимации имеющихся экспериментальных данных о поведении выходных параметров объекта

моделирования в зависимости от входных параметров и воздействий внешней среды, а также от значений внутренних параметров объекта.

Однако область применения моделей подобного типа ограничена. Для создания математических моделей сложных систем и процессов, применимых для широкого класса реальных задач требуется, как уже отмечалось выше, привлечение большого объема знаний, накопленных в рассматриваемой дисциплине (а в некоторых случаях и в смежных областях). В большинстве дисциплин (особенно естественнонаучных) эти знания сконцентрированы в аксиомах, законах, теоремах, имеющих четкую математическую формулировку.

Следует отметить, что во многих областях знаний (механике, физике, биологии и т.д.) принято выделять законы, справедливые для всех объектов исследования данной области знаний, и соотношения, описывающие поведение отдельных объектов или их совокупностей. К числу первых в физике и механике относятся, например, уравнения баланса массы, количества движения, энергии и т.д., справедливые при определенных условиях для любых материальных тел, независимо от их конкретного строения, структуры, состояния, химического состава. Уравнения этого класса подтверждены огромным количеством экспериментов, хорошо изучены и в силу этого применяются в соответствующих математических моделях как данность. Соотношения второго класса в физике и механике называют определяющими, или физическими уравнениями, или уравнениями состояния. Они устанавливают особенности поведения материальных объектов или их совокупностей (например, жидкостей, газов, упругих или пластических сред и т.д.) при воздействиях различных внешних факторов.

В качестве классических примеров определяющих соотношений можно привести закон Гука в теории упругости или уравнение Клапейрона для идеальных газов. Очевидно, определяющие соотношения должны отражать реальное атомно-молекулярное строение исследуемых материальных объектов.

Соотношения второго класса гораздо менее изучены, а в ряде случаев их приходится устанавливать самому исследователю (особенно при анализе объектов, состоящих из новых материалов). Необходимо отметить, что определяющие соотношения – это основной элемент, «сердцевина» любой математической модели физико-механических процессов. Именно ошибки в выборе или установлении определяющих соотношений приводят к количественно (а в некоторых случаях и качественно) неверным результатам моделирования.

Совокупность математических соотношений указанных двух классов определяет оператор модели. В большинстве случаев оператор модели включает в себя систему обыкновенных дифференциальных уравнений (ОДУ), дифференциальных уравнений в частных производных (ДУЧП) и/или интегро-дифференциальных уравнений (ИДУ). Для обеспечения корректности постановки задачи к системе ОДУ или ДУЧП добавляются начальные и/или граничные условия, которые, в свою очередь, могут быть алгебраическими или дифференциальными соотношениями различного порядка.

Можно выделить несколько наиболее распространенных типов задач для систем ОДУ или ДУЧП:

задача Коши, или задача с начальными условиями, в которой по заданным в начальный момент времени переменным (начальным условиям) определяются значения этих искомых переменных для любого момента времени;

начально-граничная, или краевая, задача, когда условия на искомую функцию выходного параметра задаются в начальный момент времени для всей пространственной области и на границе последней в каждый момент времени (на исследуемом интервале);

задачи на собственные значения, в формулировку которых входят неопределенные параметры, определяемые из условия качественного изменения поведения системы (например, потеря устойчивости состояния равновесия или стационарно го движения, появление периодического режима, резонанс и т.д.).

Для контроля правильности полученной системы математических соотношений требуется проведение ряда обязательных проверок.

Контроль размерностей, включающий правило, согласно которому приравниваться и складываться могут только вели чины одинаковой размерности. При переходе к вычислениям данная проверка сочетается с контролем использования одной и той же системы единиц для значений всех параметров.

Контроль порядков, состоящий из грубой оценки сравнительных порядков складываемых величин и исключением мало значимых параметров.

Контроль характера зависимостей заключается в проверке того, что направление и скорость изменения выходных параметров модели, вытекающие из выписанных математических соотношений, такие, как это следует непосредственно из «физического» смысла изучаемой модели.

Контроль экстремальных ситуаций – проверка того, какой вид принимают математические соотношения, а также результаты моделирования, если параметры модели или их комбинации приближаются к предельно допустимым для них значениям, чаще всего к нулю или бесконечности. В подобных экстремальных ситуациях модель часто упрощается, математические соотношения приобретают более наглядный смысл, упрощается их проверка. Например, в задачах механики де формируемого твердого тела деформация материала в исследуемой области в изотермических условиях возможна лишь при приложении нагрузок, отсутствие же нагрузок должно приводить к отсутствию деформаций.

Контроль граничных условий, включающий проверку того, что граничные условия действительно наложены, что они использованы в процессе построения искомого решения и что значения выходных параметров модели на самом деле удовлетворяют данным условиям.

Контроль физического смысла – проверка физического или иного, в зависимости от характера задачи, смысла исходных и промежуточных соотношений, появляющихся по мере конструирования модели.

Контроль математической замкнутости, состоящий в проверке того, что выписанная система математических соотношений дает возможность, притом однозначно, решить поставленную математическую задачу. Например, если задача свелась к отысканию п неизвестных из некоторой системы алгебраических или трансцендентных уравнений, то контроль замкнутости состоит в проверке того факта, что число независимых уравнений должно быть п. Если их меньше п, то надо установить недостающие уравнения, а если их больше п, то либо уравнения зависимы, либо при их составлении допущена ошибка. Однако если уравнения получаются из эксперимента или в результате наблюдений, то возможна постановка задачи, при которой число уравнений превышает п, но сами уравнения удовлетворяются лишь приближенно, а решение ищется, например, по методу наименьших квадратов. Неравенств среди условий также может быть любое число, как это бывает, например, в задачах линейного программирования.

Свойство математической замкнутости системы математических соотношений тесно связано с введенным Ж. Адамаром понятием корректно поставленной математической задачи, т.е. задачи, для которой решение существует, оно единственно и непрерывно зависит от исходных данных. В данном случае решение считается непрерывным, если малому изменению исходных данных соответствует достаточно малое изменение решения.

Понятие корректности задачи имеет большое значение в прикладной математике. Например, численные методы решения оправдано применять лишь к корректно поставленным задачам. При этом далеко не все задачи, возникающие на практике, можно считать корректными (например, так называемые обратные задачи). Доказательство корректности конкретной математической задачи - достаточно сложная проблема, она решена только для некоторого класса математически поставленных задач. Проверка математической замкнутости является менее сложной по сравнению с проверкой корректности математической постановки. В настоящее время активно исследуются свойства некорректных задач, разрабатываются методы их решения. Аналогично понятию «корректно поставленная задача» можно ввести понятие «корректная математическая модель».

Математическая модель является корректной, если для нее осуществлен и получен положительный результат всех контрольных проверок: размерности, порядков, характера зависимостей, экстремальных ситуаций, граничных условий, физического смысла и математической замкнутости.

Существование и единственность решения задачи Коши доказана математиками. Поэтому данную математическую модель можно считать корректной.

Математическая постановка задачи еще более абстрактна, чем концептуальная, так как сводит исходную задачу к чисто математической (например, к задаче Коши), методы решения которой достаточно хорошо разработаны. Умение свести исходную проблему к известному классу математических задач и обосновать правомочность такого сведения требует высокой квалификации математика-прикладника и особенно высоко ценится в исследовательских коллективах.

2.5.5. Выбор и обоснование выбора метода решения задачи

При использовании разработанных математических моделей, как правило, требуется найти зависимость некоторых неизвестных заранее параметров объекта моделирования (например, координат и скорости центра масс тела, точности броска), удовлетворяющих определенной системе уравнений. Таким образом, поиск решения задачи сводится к отысканию некоторых зависимостей искомых величин от исходных параметров модели. Как уже было отмечено выше, все методы решения задач, составляющих «ядро» математических моделей, можно подразделить на аналитические и алгоритмические.

Следует отметить, что при использовании аналитических решений для получения результатов «в числах» также часто требуется разработка соответствующих алгоритмов, реализуемых на ЭВМ. Однако исходное решение при этом представляет собой аналитическое выражение (или их совокупность). Решения же, основанные на алгоритмических методах, принципиально не сводимы к точным аналитическим решениям рассматриваемой задачи.

Выбор того или иного метода исследования в значительной степени зависит от квалификации и опыта членов рабочей группы. Как уже было отмечено, аналитические методы более удобны для последующего анализа результатов, но применимы лишь для относительно простых моделей. В случае, если математическая задача (хотя бы и в упрощенной постановке) допускает аналитическое решение, последнее, без сомнения, предпочтительнее численного.

Алгоритмические методы сводятся к некоторому алгоритму, реализующему вычислительный эксперимент с использованием ЭВМ. Точность моделирования в подобном эксперименте существенно зависит от выбранного метода и его параметров (например, шага интегрирования). Алгоритмические методы, как правило, более трудоемки в реализации, требуют от членов рабочей группы хорошего знания методов вычислительной математики, обширной библиотеки специального программного обеспечения и мощной вычислительной техники. Современные модели на базе алгоритмических методов разрабатываются в исследовательских организациях, которые зарекомендовали себя как авторитетные научные школы в соответствующей области знания.

Как отмечалось ранее, приближенные и численные методы исследования поставленных математических задач относятся к обширному разделу – современной вычислительной математике. Численные методы применимы лишь для корректных математических задач, что существенно ограничивает использование их в математическом моделировании.

Общим для всех численных методов является сведение математической задачи к конечномерной. Это чаще всего достигается дискретизацией исходной задачи, т.е. переходом от функции непрерывного аргумента к функциям дискретного аргумента. Например, траектория центра тяжести баскетбольного мяча определяется не как непрерывная функция времени, а как табличная (дискретная) функция координат от времени, т.е. определяющая значения координат лишь для конечного числа моментов времени. Полученное решение дискретной задачи принимается за приближенное решение исходной математической задачи.

Применение любого численного метода неминуемо приводит к погрешности результатов решения задачи. Выделяют три основных составляющих возникающей погрешности при численном решении исходной задачи:

неустранимая погрешность, связанная с неточным заданием исходных данных (начальные и граничные условия, коэффициенты и правые части уравнений);

погрешность метода, связанная с переходом к дискретному аналогу исходной задачи (например, заменяя производную разностным аналогом);

ошибка округления, связанная с конечной разрядностью чисел, представляемых в ЭВМ.

Естественным требованием для конкретного вычислительного алгоритма является согласованность в порядках величин перечисленных трех видов погрешностей.

Численный, или приближенный, метод реализуется всегда в виде вычислительного алгоритма. Поэтому все требования, предъявляемые к алгоритму, применимы и к вычислительному алгоритму. Прежде всего, алгоритм должен быть реализуем – обеспечивать решение задачи за допустимое машинное время. Важной характеристикой алгоритма является его точность, т.е. возможность получения решения исходной задачи с заданной точностью за конечное число действий. Очевидно, чем меньше е, тем больше затрачиваемое машинное время. Для очень малых значений е время вычислений может быть недопустимо большим. Поэтому на практике добиваются некоторого компромисса между точностью и затрачиваемым машинным временем. Очевидно, что для каждой задачи, алгоритма и типа ЭВМ имеется свое характерное значение достигаемой точности.

Время работы алгоритма зависит от числа действий, необходимых для достижения заданной точности. Для любой математической задачи, как правило, можно предложить несколько алгоритмов, позволяющих получить решение с заданной точностью, но за разное число действий. Алгоритмы, включающие меньшее число действий для достижения одинаковой точности, будем называть более экономичными, или более эффективными.

В процессе работы вычислительного алгоритма на каждом акте вычислений возникает некоторая погрешность. При этом от действия к действию она может возрастать или не возрастать (а в некоторых случаях даже уменьшаться). Если погрешность в процессе вычислений неограниченно возрастает, то такой алгоритм называется неустойчивым, или расходящимся. В противном случае алгоритм называется устойчивым, или сходящимся.

Выше уже отмечалось, что вычислительная математика объединяет огромный пласт разнообразных, быстро развивающихся численных и приближенных методов, поэтому практически невозможно привести их законченную классификацию. Стремление получить более точные, эффективные и устойчивые вычислительные алгоритмы приводит к появлению многочисленных модификаций, учитывающих специфические особенности конкретной математической задачи или даже особенности моделируемых объектов.

Можно выделить следующие группы численных методов по объектам, к которым они применяются:

интерполяция и численное дифференцирование;

численное интегрирование;

определение корней линейных и нелинейных уравнений;

решение систем линейных уравнений (подразделяют на прямые и итерационные методы);

решение систем нелинейных уравнений;

решение задачи Коши для обыкновенных дифференциальных уравнений;

решение краевых задач для обыкновенных дифференциальных уравнений;

решение уравнений в частных производных;

решение интегральных уравнений.

Огромное разнообразие численных методов в значительной степени затрудняет выбор того или иного метода в каждом конкретном случае. Поскольку для реализации одной и той же модели можно использовать несколько альтернативных алгоритмических методов, то выбор конкретного метода производится с учетом того,

какой из них больше подходит для данной модели с точки зрения обеспечения эффективности, устойчивости и точности результатов, а также более освоен и знаком членам рабочей группы. Освоение нового метода, как правило, очень трудоемко и связано с большими временными и финансовыми затратами. При этом основные затраты связаны с разработкой и отладкой необходимого программного обеспечения для соответствующего класса ЭВМ, обеспечивающего реализацию данного метода.

Следует отметить, что вычислительная математика в определенном смысле являет собой более искусство, нежели науку (в понимании последней как области культуры, базирующейся на формальной логике). Очень часто эффективность применяемых методов, разработанных программ определяется нарабатываемыми годами и десятками лет интуитивными приемами, не обоснованными с математических позиций. В связи с этим эффективность одного и того же метода может весьма существенно отличаться при его применении различными исследователями.

2.5.6. Реализация математической модели в виде программы для ЭВМ

При создании различных программных комплексов, используемых для решения разнообразных исследовательских, проектно-конструкторских и управленческих задач, в настоящее время, основой, как правило, служат математические модели. В связи с этим возникает необходимость реализации модели в виде программы для ЭВМ. Процесс разработки надежного и эффективного программного обеспечения является не менее сложным, чем все предыдущие этапы создания математической модели. Успешное решение данной задачи возможно лишь при уверенном владении современными алгоритмическими языками и технологиями программирования, знании возможностей вычислительной техники, имеющегося программного обеспечения, особенностей реализации на ЭВМ методов вычислительной математики, наличии опыта решения подобных задач.

Процесс создания программного обеспечения можно разбить на ряд этапов:

составление технического задания на разработку пакета про грамм программного обеспечения;

проектирование структуры программного комплекса;

кодирование алгоритма;

тестирование и отладка;

сопровождение и эксплуатация.

Техническое задание на разработку программного обеспечения оформляют в виде спецификации. Примерная форма спецификации включает следующие семь разделов:

1. 
   Название задачи – дается краткое определение решаемой за дачи, название программного комплекса, указывается система программирования для его реализации и требования к аппаратному обеспечению (компьютеру, внешним устройствам и т.д.).
   
2. 
   Описание – подробно излагается математическая постановка задачи, описываются применяемая математическая модель для задач вычислительного характера, метод обработки входных данных для задач не вычислительного (логического) характера и т.д.
   

3. 
   Управление режимами работы программы – формируются основные требования к способу взаимодействия пользователя с программой (интерфейс «пользователь-компьютер»).
   
4. 
   Входные данные – описываются входные данные, указываются пределы, в которых они могут изменяться, значения, которые они не могут принимать, и т.д.
   
5. 
   Выходные данные – описываются выходные данные, указывается, в каком виде они должны быть представлены (в числовом, графическом или текстовом), приводятся сведения о точности и объеме выходных данных, способах их сохранения и т.д.
   
6. 
   Ошибки - перечисляются возможные ошибки пользователя при работе с программой (например, ошибки при вводе входных данных), указываются способы диагностики (в данном случае под диагностикой понимается выявление, обнаружение ошибок при работе программного комплекса) и защиты от этих ошибок на этапе проектирования, а также возможная реакция пользователя при совершении им ошибочных действий и реакция программного комплекса (компьютера) на эти действия.
   
7. 
   Тестовые задачи – приводятся один или несколько тестовых примеров, на которых в простейших случаях проводится отладка и тестирование программного комплекса.
   

На этапе проектирования формируется общая структура программного комплекса. Вся программа разбивается на программные модули. Для каждого программного модуля формулируются требования по реализуемым функциям и разрабатывается алгоритм, выполняющий эти функции. Определяется схема взаимодействия программных модулей, называемая схемой потоков данных программного комплекса. Разрабатывается план и задаются исходные данные для тестирования отдельных модулей и программного комплекса в целом.

Большинство программ, реализующих математические модели, состоят из трех основных частей:

препроцессора (подготовка и проверка исходных данных модели);

процессора (решение задачи, реализация вычислительного эксперимента);

постпроцессора (отображение полученных результатов).

Лишь для относительно простых случаев эти три составные части могут быть оформлены в виде одной программы. При решении современных задач по моделированию поведения жидкостей, газов и твердых тел каждая из частей может включать в себя целый комплекс программ. Например, постпроцессор должен уметь представлять информацию не только в табличном, но и графическом виде (диаграммы, графики зависимости от различных параметров, отображение скалярных, векторных (тензорных) полей и т.п.). Возможности пре- и постпроцессора наиболее широко реализуются в современных системах автоматизированного проектирования (САПР), где они в значительной степени могут сократить время на получение данных и оценку результатов моделирования.

Как правило, создание современных математических моделей в какой-либо области и доведение их до программных комплексов требует значительных временных затрат (минимум 3–5 лет). Требуется время не только на освоение методик и подходов к моделированию в исследуемой области, но и на наработку библиотек программ по решению возникающих математических задач, по подготовке исходных данных и отображению получаемых результатов. Качественные, надежные, обладающие дружественным интерфейсом, легко модифицируемые и хорошо сопровождаемые программные комплексы можно создавать лишь при наличии хорошо продуманной стратегии развития программного обеспечения, обеспечивающей его модульность и совместимость по входным и выходным параметрам.

Большое значение следует придавать освоению современных технологий программирования: структурной, абстрактной, объектно-ориентированной и визуальной. Назначение любой технологии - это в первую очередь повышение надежности программного обеспечения и увеличение производительности труда программиста. Причем чем серьезней и объемней программный проект, тем большее значение приобретают вопросы использования современных технологий программирования. Пренебрежение данными вопросами может привести к значительным временным издержкам и снижению надежности программного комплекса.

Важнейшим фактором, определяющим надежность и малые сроки создания программного комплекса для решения конкретного класса задач, является наличие развитой библиотеки совместимых между собой программных модулей. Программа получается более надежной и создается за меньшие сроки при максимальном использовании стандартных программных элементов. Для эффективной разработки программного обеспечения в области математического моделирования необходимо обратить внимание на создание следующих стандартных библиотек программ:

приближенные и численные методы (процессоры);

средства подготовки исходных данных (препроцессоры);

средства визуализации и представления результатов (постпроцессоры).

Разработка таких общих библиотек программ возможна лишь при стандартизации потоков передачи данных между препроцессором, процессором и постпроцессором. В простейшем случае речь может идти об унификации форматов передаваемых файлов.

2.5.7. Проверка адекватности модели

Под адекватностью математической модели будет пониматься степень соответствия результатов, полученных по разработанной модели, данным эксперимента или тестовой задачи. Прежде чем переходить к проверке адекватности модели, необходимо убедиться в правильном комплексном функционировании всех алгоритмов и программ модели, выполнить независимое тестирование и отладку всех отдельных алгоритмов (например, используемых программных модулей, реализующих используемый численный метод).

Проверка адекватности модели преследует две цели:

1. 
   убедиться в справедливости совокупности гипотез, сформулированных на этапах концептуальной и математической постановок. Переходить к проверке гипотез следует лишь после проверки использованных методов решения, комплексной отладки и устранения всех ошибок и конфликтов, связанных с программным обеспечением;
   
2. 
   установить, что точность полученных результатов соответствует точности, оговоренной в техническом задании.
   

Проверка разработанной математической модели выполняется путем сравнения с имеющимися экспериментальными данными о реальном объекте или с результатами других, созданных ранее и хорошо себя зарекомендовавших моделей. В первом случае говорят о проверке путем сравнения с экспериментом, во втором – о сравнении с результатами решения тестовой задачи.

Решение вопроса о точности моделирования зависит от требований, предъявляемых к модели, и ее назначения. При этом должна учитываться точность получения экспериментальных результатов или особенности постановок тестовых задач. В моделях, предназначенных для выполнения оценочных и прикидочных расчетов, удовлетворительной считается точность 10–15%. В моделях, используемых в управляющих и контролирующих системах, требуемая точность может быть 1–2% и даже более.

Как правило, различают качественное и количественное совпадение результатов сравнения. При качественном сравнении требуется лишь совпадение некоторых характерных особенностей в распределении исследуемых параметров (например, наличие экстремальных точек, положительное или отрицательное значение параметра, его возрастание или убывание и т.д.). Фактически при качественном сравнении оценивается совпадение лишь вида функции распределения параметров (убывающая или возрастающая, с одним экстремумом или с несколькими). Вопрос о количественном сравнении можно ставить лишь после удовлетворительного ответа на вопрос о качественном соответствии результатов. При количественном сравнении большое значение следует придавать точности исходных данных для моделирования и соответствующих им значений сравниваемых параметров.

Неадекватность результатов моделирования возможна, по крайней мере, по трем причинам:

а) значения задаваемых параметров модели не соответствуют допустимой области этих параметров, определяемой принятой системой гипотез;

б) принятая система гипотез верна, но константы и параметры в использованных определяющих соотношениях установлены не точно.

в) неверна исходная совокупность гипотез.

Все три случая требуют дополнительного исследования как моделируемого объекта (с целью накопления новой дополнительной информации о его поведении), так и исследования самой модели (с целью уточнения границ ее применимости).

В данном случае не анализируется влияние выбранного численного метода на точность получаемого решения, а значит, и на адекватность модели. Вопрос о сходимости алгоритма и устойчивости получаемого выбранным численным методом решения, а также накопление погрешностей, связанных с ошибками округления при использовании ЭВМ, здесь не рассматривается.

При возникновении проблем, связанных с адекватностью модели, ее корректировку требуется начинать с последовательного анализа всех возможных причин, приведших к расхождению результатов моделирования и результатов эксперимента. В первую очередь требуется исследовать модель и оценить степень ее адекватности при различных значениях варьируемых параметров (начальных и граничных условиях, параметров, характеризующих свойства объектов моделирования). Если модель неадекватна в интересующей исследователя области параметров, то можно попытаться уточнить значения констант и исходных параметров модели. Если же и в этом случае нет положительных результатов, то единственной возможностью улучшения модели остается изменение принятой системы гипотез. Данное решение фактически означает возвращение ко второму этапу процесса разработки модели и может повлечь не только серьезное изменение математической постановки задачи, но и методов ее решения (например, переход от аналитических к численным), полной переработки программного обеспечения и нового цикла проверки модели на адекватность. Поэтому решение об изменении принятой системы гипотез должно быть всесторонне взвешено и приниматься только в том случае, если исчерпаны все прочие возможности по улучшению адекватности модели.

Надлежит предостеречь начинающих исследователей от попыток «перепрыгнуть» рассмотренный этап моделирования, от желания быстрее перейти к решению «настоящей задачи». Как показывает собственный опыт авторов, подобный образ действий приводит к огромным временным издержкам (не говоря уже о психологических). Особенно опасной является ситуация, в которой при решении реальной задачи с использованием не проверенной должным образом модели получаются правдоподобные результаты. Для других условий модель может дать качественно неверные результаты, но истоки ошибок разработчики будут искать уже не в модели.

2.5.8. Практическое использование построенной модели и анализ результатов моделирования

Дескриптивные модели, рассмотренные выше, предназначены для описания исследуемых параметров некоторого явления или процесса, а также для изучения закономерностей изменения этих параметров. Эти модели могут использоваться:

для изучения свойств и особенностей поведения исследуемого объекта при различных сочетаниях исходных данных и разных режимах;

как моделирующие блоки в различных САПР и автоматизированных системах управления (АСУ);

при построении оптимизационных моделей и моделей - имитаторов сложных систем и комплексов.

Модели, разрабатываемые для исследовательских целей, как правило, не доводятся до уровня программных комплексов, предназначенных для передачи сторонним пользователям. Время их существования чаще всего ограничено временем выполнения исследовательских работ по соответствующему направлению. Эти модели отличает поисковый характер, применение новых вычислительных процедур и алгоритмов, неразвитый программный интерфейс.

Модели и построенные на их основе программные комплексы, предназначенные для последующей передачи сторонним пользователям или коммерческого распространения, имеют развитый дружественный интерфейс, мощные пре- и постпроцессоры. Данные модели обычно строятся на апробированных и хорошо себя зарекомендовавших постановках и вычислительных процедурах. Программные комплексы имеют подробные и качественно составленные описания и руководства для пользователя; по всем неясным вопросам фирма-производитель проводит консультации. Однако следует помнить, что такие коммерческие модели предназначены только для решения четко оговоренного класса задач. Как правило, они не могут быть модернизированы и усовершенствованы. Так, пользователь не имеет возможности самостоятельно расширять библиотеку используемых численных методов или изменять систему исходных гипотез.

Независимо от области применения созданной модели группа разработчиков обязана провести качественный и количественный анализ результатов моделирования.

Работая с моделью, разработчики становятся специалистами в области, связанной с объектом моделирования. Они достаточно хорошо представляют свойства объекта, могут предсказать и объяснить его поведение. Поэтому всесторонний анализ результатов моделирования позволяет:

выполнить модификацию рассматриваемого объекта, найти его оптимальные характеристики или, по крайней мере, лучшим образом учесть его поведение и свойства;

обозначить область применения модели, что особенно важно в случае использования моделей для систем автоматического управления;

проверить обоснованность гипотез, принятых на этапе математической постановки, оценить возможность упрощения модели с целью повышения ее эффективности при сохранении требуемой точности;

показать, в каком направлении следует развивать модель в дальнейшем.

2.5.9. Вопросы для самопроверки

Кто участвует в разработке содержательной постановки задачи?

На основании какой информации выполняется формулировка концептуальной постановки задачи моделирования?

Какие функции выполняет постановщик задач?

Какая из постановок задачи (содержательная, концептуальная или математическая) является самой абстрактной?

Что включает понятие корректности математической задачи?

Каким условиям должна удовлетворять корректная модель?

К каким математическим задачам можно применять численные методы?

Назовите три составляющие погрешности численных методов.

Какие цели преследует проверка адекватности модели?

Перечислите причины возможной неадекватности модели.

Для решения каких задач может быть использована математическая модель?

Выполните содержательную, концептуальную и математическую постановки для математической модели, описывающей взлет космического аппарата с Луны.

Выполните содержательную, концептуальную и математическую постановки для математической модели, описывающей посадку спутника в атмосфере Земли.

Выполните содержательную, концептуальную и математическую постановки для математической модели, описывающей движение шарика в сферической ямке. Выберите и реализуйте метод решения полученной математической задачи. Исследуйте траектории шарика в зависимости от начальных условий.

Выполните содержательную, концептуальную и математическую постановки для математической модели, описывающей движение срубленного дерева.

Выполните содержательную, концептуальную и математическую постановки для математической модели, описывающей движение заряженной частицы в магнитном поле.

Космический аппарат совершает движение по орбите вокруг Земли и может быть виден некоторым наблюдателем, находящимся на ее поверхности в точке с заданными координатами. Выполните содержательную, концептуальную и математическую постановки для математической модели, описывающей движение космического аппарата по небосводу Земли с точки зрения наблюдателя.

Выполните содержательную, концептуальную и математическую постановки для математической модели, описывающей движение лыжника, выполняющего прыжок с трамплина.

Выполните содержательную, концептуальную и математическую постановки для математической модели, описывающей процесс нагревания и закипания чайника.

Разработайте математическую модель какого-либо процесса в интересующей вас области знаний, опишите особенности каждого из этапов моделирования, сравните их с этапами построения математической модели предыдущего задания.