лекцииММиИТпП-ч.1. Конспект лекций ч. 1 Омск

• Название: Конспект лекций ч. 1 Омск
• Дата: 15.11.2021
• Размер: 1.27 Mb.
• Имя файла: лекцииММиИТпП-ч.1.docx
• Тип: Конспект; #273057
• страница: 12 из 16

3. Структурные модели

Важно отметить, что при установлении различных связей между элементами могут возникать новые свойства построенной модели, которыми не обладает каждый из элементов в отдельности. Эти так называемые «системные» свойства модели, появляющиеся при объединении отдельных элементов в одно целое, играют важную роль в моделировании сложных систем, так как позволяют исследовать новые качества объекта с помощью вычислительного эксперимента. Поэтому важно знать общие правила построения структурных моделей, которые приводятся в данной главе и иллюстрируются на нескольких примерах, взятых из различных областей целенаправленной деятельности человека.

Как было отмечено выше, одним из важных этапов математического моделирования является переход от содержательной (технической) и концептуальной постановок задачи к математической, т.е. переход с технического языка (или – «языка природы») описания исследуемого объекта к языку математических формул и уравнений. Однако на практике такой переход бывает совсем не просто осуществить. В некоторых случаях это связано со сложностью самого исследуемого объекта, в других – с отсутствием необходимой информации об объекте или соответствующего математического аппарата. Поэтому часто возникает необходимость «разбить» поставленную задачу на несколько более простых подзадач, которые имеют известные решения или которые можно решить с помощью апробированных методов.

Для этой цели удобно использовать методы структурного моделирования, позволяющие еще на стадии постановки упростить решаемую задачу путем исследования внутренней структуры рассматриваемого объекта, изучения свойств отдельных элементов объекта и связей между ними. При этом следует отметить, что важное значение имеет способ разбиения исследуемого объекта на отдельные элементы и установление связей между ними, которые зависят от целей моделирования. Очевидно, что такое разбиение неоднозначно. Чем сложнее исходная задача, тем больше элементов необходимо вводить в рассмотрение и учитывать огромное количество связей между ними. Это обычно приводит к многоуровневым структурным схемам древовидной формы с различной иерархией элементов, которую необходимо учитывать при математическом моделировании. При этом структурные схемы, связи подсистем и их элементов несложно изобразить графически, что делает анализируемые объекты более понятными, «прозрачными».

3.1. Что такое структурная модель?

Очень часто для достижения практических целей возникает необходимость рассматривать исследуемый объект как совокупность отдельных элементов, связанных (взаимодействующих) между собой некоторым образом, в то же время взаимодействующих с окружающим миром как нечто целое. В этом случае исследуемый объект удобно представить в виде системы, а при его моделировании использовать методы системного анализа.

Напомним основные понятия системного анализа, которые будут использоваться в дальнейшем. Одним из основополагающих понятий системного анализа является понятие искусственной системы, которую определим следующим образом.

Система есть совокупность взаимосвязанных элементов, выделенных из среды и взаимодействующих с окружающей средой как целое для достижения поставленной цели.

Следует отметить, что важным признаком для выделения системы из среды является возможность определения взаимодействия этой системы с окружением независимо от поведения ее отдельных элементов (именно это подразумевается под словами «взаимодействующая ... как целое»). Выделяет систему из среды исследователь, который отделяет ее элементы от среды в соответствии с поставленной целью. Под средой здесь понимается совокупность всех объектов, изменение свойств которых влияет на систему, а также тех объектов, чьи свойства изменяются в результате поведения системы.

Из приведенных определений видно, насколько важна роль исследователя – он формулирует цели, выделяет систему и определяет среду. При этом сам может отнести себя к среде и строить изолированные системы, включить себя в систему и строить ее с учетом своего влияния на ее функционирование (адаптивные системы), а также выделить себя и из системы, и из среды, рассматривая систему как открытую или развивающуюся. В принципе исследователя можно не рассматривать как элемент системы или среды, но, дополнительное введение исследователя помогает при построении систем и их классификации. Для описания систем в системном анализе рассматриваются четыре основные модели. Если внутреннее строение системы неизвестно (или не интересует исследователя), то применяется модель «черного ящика». В этой модели системы отсутствуют (или не используются в явной форме) сведения о внутреннем содержании «ящика» (поэтому он и называется «черным»), а только задаются входные и выходные связи со средой. Обычно это сводится к заданию двух множеств входных и выходных параметров, но никаких соотношений между ними не задается. Примером модели «черного ящика» может служить экспериментальное исследование некоторого сложного объекта, когда экспериментатор, изменяя входные пара метры объекта, получает на выходе различные его характеристики. Очевидно, что исследование внутреннего устройства системы невозможно с помощью модели «черного ящика»; применение последней можно считать оправданным лишь на самых ранних этапах исследования нового объекта. Для этого необходимы более развитые модели. Одной из таких моделей является модель состава системы, описывающая, из каких элементов и подсистем состоит данная система. При этом элементами системы называются те ее части, которые полагаются неделимыми; части, состоящие более чем из одного элемента, называются подсистемами. Например, если в качестве системы рассмотреть автомобиль, то ее подсистемой можно считать систему управления, а элементами последней – руль, педали и т.д.

Сложность построения модели состава системы состоит в ее неоднозначности. Это можно объяснить следующим образом. Во-первых, понятие «элементарности» можно определять по-разному. Во-вторых, модель состава (как и любая другая модель) является целевой и для отличающихся целей один и тот же объект может потребовать различного разбиения на части. В-третьих, всякое разбиение целого на части является относительным. Например, тормозную подсистему автомобиля можно отнести как к ходовой части, так и к подсистеме управления.

В большинстве случаев модели состава системы оказывается недостаточно для ее описания. Мало знать состав системы, кроме этого необходимо установить связи между отдельными элементами, которые называются отношениями. Совокупность необходимых и достаточных для достижения цели отношений между элементами называется моделью структуры системы. Основной сложностью при описании структуры (списка отношений) является обоснование конечного числа связей, наиболее существенных по отношению к рассматриваемой цели. Например, при моделировании механической системы, движущейся в околоземном пространстве, обычно не учитываются силы взаимного притяжения отдельных материальных точек (элементов), но учитывается сила притяжения к Земле (отношения).

Следует отметить, что структура системы является абстрактной моделью, так как рассматривает только связи (отношения) между элементами, а не сами элементы (понятно, что на практике говорить об отношениях без элементов просто не имеет смысла). Однако в некоторых случаях модель структуры теоретически может быть исследована отдельно, если, например, отношения заданы в виде математических формул или уравнений.

Теперь, имея три формальные модели системы - «черного ящика», состава и структуры - и объединив их, можно получить еще одну модель, которую называют структурной схемой системы, или моделью «белого ящика». Данная модель включает все элементы системы, все связи между элементами внутри системы и связи системы (или ее отдельных элементов) с окружающей средой (входы и выходы системы), как изображено на рис. 3.1. Заметим, что под «всеми» элементами и связями понимаются, конечно, значимые с точки зрения цели и задач разрабатываемой модели.

Следует отметить, что структурная схема системы является формальной моделью, отделенной от содержательного наполнения. Это позволяет рассматривать ее как особый математический объект и исследовать его свойства. Такой объект называется графом. Он состоит из обозначений элементов произвольной природы, называемых вершинами, и обозначений связей между ними, называемых ребрами.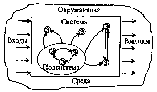


Рис. 3.1. Структурная схема системы
На рис. 3.2 приведен пример графа, у которого вершины обозначены в виде кружочков, а ребра - в виде линий. Стрелки указывают на несимметричность некоторых связей. Такой граф называется ориентированным. Каждая пара вершин может быть соединена с любым числом ребер. Чтобы ввести другие различия между ребрами, кроме несимметричности, им приписывают различные веса. Такие графы называются взвешенными. В качестве весов могут выступать различные характеристики графа, например длина ребра, число каналов электросети, тип покрытия в сети автомобильных дорог и т.д.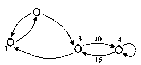


Рис. 3.2. Пример графа
В настоящее время для графов разработана целая теория, имеющая многочисленные приложения. Графы могут изображать любые структуры. Некоторые графы получили специальные названия: линейные, древовидные (иерархические), сетевые, матричные и т.д. Пример сетевого графа приведен на рис. 4.3.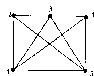


Рис 3.3. Сетевой граф
Как отмечено выше, граф (структурная схема) является формальной моделью, которую необходимо наполнить конкретным содержанием. Только после этого структурная схема становится структурной моделью исследуемого объекта. Например, если в качестве вершин графа, изображенного на рис. 3.3, считать цилиндрические шарниры, а ребер - прямолинейные стержни, то получим структурную модель стержневой конструкции, широко применяемую при моделировании в строительной механике. Если же в качестве вершин рассматривать узлы связи, а за ребра принять линии связи, то получим структурную модель сети электросвязи.

Таким образом, можно дать следующее определение структурной модели.

Структурная модель системы – это совокупность конкретных элементов данной системы, необходимых и достаточных отношений между этими элементами и связей между системой и окружающей средой.

Рассмотрим пример построения структурной модели, поясняющий это определение. Пусть требуется построить структурную модель абсолютно твердого тела, совершающего поступательное движение под действием приложенной силы (рис. 3.4). Напомним, что абсолютно твердое тело при движении не изменяет форму и размеры. Поэтому такое тело можно представить как совокупность материальных точек (элементов), соединенных прямолинейными невесомыми недеформируемыми стержнями.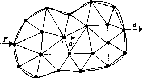


Рис. 3.4. Структурная модель абсолютно твердого тела при поступательном движении
Сила Р выступает в качестве воздействия внешней среды на тело, а откликом на это воздействие (выходным параметром) служит ускорение тела а (или любой его точки вследствие их равенства при поступательном движении).

Таким образом, для того чтобы данная структурная модель правильно описывала поступательное движение тела, необходимо и достаточно, чтобы выполнялось условие недеформируемых стержней в качестве связей между элементами (материальными точками) могут выступать пружинки с различными упругими свойствами (рис. 3.5).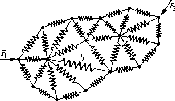


Рис. 3.5. Структурная модель упругого тела
Из последнего соотношения следует, что число элементов и их распределение внутри тела не имеют значения. Другое дело, когда необходимо описать вращательное движение твердого тела вокруг некоторой заданной оси под действием приложенного момента сил. В этом случае распределение элементов внутри объема тела должно быть таким, чтобы выполнялось условие равенства моментов инерции реального тела и его структурной модели относительно заданной оси.

Из этого равенства вытекают необходимые и достаточные условия на отношения между элементами данной структурной модели (длины и ориентации стержней, массы материальных точек), что хорошо видно из рис. 3.6.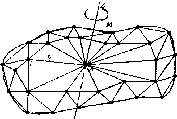


Рис. 3.6. Структурная модель вращающегося тела
Еще больше усложнится структурная модель в случае описания движения деформируемого, например упругого, тела.

В этой структурной модели для получения необходимых и достаточных отношений между элементами кроме распределения масс по объему тела необходимо учесть распределение жесткостей пружинок, чтобы совокупность последних описывала упругие свойства реального тела.

Из этого примера видно, что структурное моделирование позволяет описывать поведение довольно сложных систем. При этом чем сложнее система, тем структурное моделирование становится все более эффективным (а в некоторых случаях – просто необходимым). Например, при описании поступательного движения твердого тела структурная модель, в принципе, не нужна, так как в этом случае тело можно представить в виде одной материальной точки, масса которой равна массе тела. В других рассмотренных выше примерах структурная модель помогает описать поведение достаточно сложных механических систем с помощью взаимодействующих простейших элементов. Для некоторых механических систем структурное моделирование является едва ли не единственным способом описания их поведения. Это относится, например, к моделированию поведения структурно-неоднородных материалов (композитов, полимеров, керамик и т.д.).

Следует отметить, что той информации, которая содержится в структурной схеме системы, очень часто бывает недостаточно для исследования. Поэтому графы надо рассматривать как вспомогательный инструмент при моделировании. Главным же при структурном моделировании является установление конкретных функциональных связей между входными, внутренними и выходными параметрами. Поэтому без достаточно широкого арсенала методов математического моделирования здесь также не обойтись. В большинстве случаев приходится составлять уравнения, описывающие поведение каждого элемента структуры с учетом взаимодействия всех элементов. Это приводит к необходимости решения систем уравнений с большим числом переменных. Однако с появлением современной вычислительной техники такие подходы к моделированию сложных систем становятся все более распространенными. В заключение данного параграфа кратко остановимся на классификации структурных моделей и примерах их применения.

Структурные модели бывают четырех видов: пространственные, временные, физические и иерархические.

Пространственные структуры обычно используют для описания геометрии исследуемого объекта и расположения в пространстве его отдельных элементов. Такие структуры хорошо описываются с помощью сетевых и матричных графов, вершины которых указывают места расположения элементов, а ребра – расстояния между ними или другие условия соединения. Пример пространственной структурной модели – структурная схема телефонной сети некоторого населенного пункта, в которой вершинами являются узлы связи, а ребрами - линии связи с указанием, например, числа каналов связи. Другим примером пространственной структуры может служить конечно-элементная сетка, с помощью которой описывается геометрия исследуемого объекта при его, например, прочностном расчете методом конечных элементов.

Временные структурные модели широко используются в сетевом и календарном планировании, а также в теории массового обслуживания. Во временных структурах в качестве элементов выступают этапы происходящего процесса или состояния системы в некоторый момент времени. Отношениями здесь служат условия перехода от одного этапа к другому или из одного состояния системы в другое. Например, на производстве широко применяют так называемые сетевые графики (технологические карты). Они представляют собой графы, вершинами которых служат необходимые производственные операции, а с помощью ребер указывается последовательность и длительность этих операции. При моделировании систем массового обслуживания удобно применять структурную схему «гибели и размножения», которая представляет собой линейный граф (последовательный набор состояний системы, вытянутый в одну цепочку). Считается, что система обслуживает случайный поток заявок, поступающих в нее. Тогда отношениями между элементами системы (ее состояниями в различные моменты времени) служат условия поступления новой заявки, которые можно характеризовать, например, интенсивностью соответствующих случайных потоков событий.

Физические структурные модели применяются для описания сложных физических свойств исследуемого объекта с помощью простых структурных элементов. Пример моделирования упругих свойств тела был приведен выше.

Для моделирования управляемых систем широко применяются иерархические структурные схемы, предполагающие наличие нескольких уровней обработки информации и принятия решений. Основная задача иерархической структуры - распределение функций обработки информации и принятия решений между отдельными элементами. На рис. 3.7 приведен пример двухуровневой веерной иерархической структуры управления системой. В данной системе существует один привилегированный элемент, который имеет возможность управлять остальными элементами. Этот привилегированный элемент обычно называется центром (Ц), а остальные элементы – производителями (П).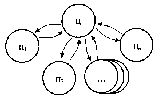

Рис. 3.7. Двухступенчатая веерная структурная схема
Отношениями в этой модели служат условия обмена информацией, денежными и материальными ресурсами между центром и производителями. Следует отметить, что в приведенной структурной схеме отношения между производителями (горизонтальные связи) отсутствуют. Неравноправие элементов системы проявляется в том, что центр назначает правила формирования воздействий на производителей и тем самым имеет возможность направлять в нужное для него русло действия нижних элементов. Данную схему несложно обобщить до многоуровневой веерной структуры, которая широко используется в экономике.

В заключение можно отметить следующее. Как было показано, структурные модели нашли широкое применение в различных областях целенаправленной деятельности человека. В некоторых случаях они помогают построить модель исследуемой системы или процесса, а иногда являются единственно эффективным инструментом при моделировании. Однако остается вопрос: «Как правильно строить структурные модели?» Постараемся дать на него ответ.

3.2. Способы построения структурных моделей

При структурном моделировании широко применяются методы анализа и синтеза. С помощью методов анализа производится разделение рассматриваемого объекта на части и исследование каждой из этих частей в отдельности. Методы синтеза, наоборот, служат для соединения частей в целое. Следует отметить, что при структурном моделировании методы анализа и синтеза необходимо применять совместно. Важно не просто разбить целое на отдельные элементы, но и соединить эти элементы таким образом, чтобы они снова образовали единое целое. С этой точки зрения синтез является завершающим этапом анализа, так как только после этого этапа можно объяснить целое через его части – в виде структуры целого. Это связано с тем, что при анализе теряются важные свойства объекта как целого (разобранный автомобиль не поедет), так и отдельных его элементов (оторванный руль «не рулит»). Поэтому, как отмечал один из ведущих специалистов по системному анализу Р. Акофф, результатом анализа является лишь вскрытие структуры системы, знание о том, как система работает, но не понимание того, почему и зачем она это делает. Только после синтеза можно объяснить поведение системы, рассматривая каждый элемент и его роль через призму всей системы.

Таким образом, анализ и синтез нельзя рассматривать как отдельные методы. Они дополняют друг друга и при структурном моделировании должны применяться совместно. Только в этом случае построенная структурная модель будет отражать основные свойства исследуемого объекта согласно поставленным целям.

Теперь рассмотрим методы анализа и синтеза более подробно. Начнем с методов анализа, которые нашли широкое применение в науке и практике. В математике давно с успехом применяются такие аналитические методы, как разложение функций в ряды, спектральный анализ, дифференциальное и интегральное исчисление; в физике – методы молекулярной динамики; на производстве – конвейерная технология изготовления.

Как было отмечено выше, основной операцией при анализе является разделение целого на части. В дальнейшем эту операцию будем называть декомпозицией и понимать под ней метод разложения системы на отдельные элементы. В результате декомпозиции исходная система распадается на подсистемы, задача – на подзадачи и т.д. При необходимости операция декомпозиции может повторяться несколько раз, что приводит к древовидным структурам системы.

Основной проблемой при декомпозиции является ее неоднозначность. Понятно, что одну и ту же систему можно разбить на различные подсистемы в зависимости как от опыта исследователя, так и от применяемой методики анализа. Поэтому в системном анализе существуют специальные критерии для обоснования процесса декомпозиции. Одним из таких критериев является полнота декомпозиции, которая в свою очередь связана с полнотой модели системы, взятой в качестве исходной при декомпозиции.

Как было указано выше, в системном анализе рассматриваются только четыре формальные модели системы: «черного ящика», состава, структуры и «белого ящика». Очевидно, что для декомпозиции подходят только последние три модели, которые позволяют рассматривать систему через взаимодействие ее отдельных элементов. Поэтому одной из проблем системного анализа является накопление наборов полных формальных моделей (полнота здесь рассматривается относительно поставленной цели) для различных исследуемых систем, получивших в теории искусственного интеллекта название фреймов.

Известны фреймы для некоторых информационных, организационных и социальных систем. Однако построение и обоснование фреймов для произвольной системы остается сложной задачей, от решения которой во многом зависит успех декомпозиции. Рассмотрим, например, педагогический процесс в высшем учебном заведении (вузе). Фреймом при декомпозиции в данном случае может служить формальная модель деятельности человека, предложенная еще К. Марксом в «Капитале» для анализа процесса труда (рис. 3.8). В качестве элементов здесь выделены: субъект деятельности, объект, на который направлена деятельность, и средства, используемые в процессе деятельности, а также все возможные связи между ними и окружающей средой. Используя эту формальную модель, можно построить модель педагогического процесса в вузе, вариант которой изображен на рис. 3.9. Здесь субъектом выступает преподаватель вуза, объектами – студенты, а средствами – методические, информационные и технические средства обучения (учебные программы изучаемых предметов, методические и учебные пособия, лабораторная база и т.д.). Окружающая среда описывается с помощью трех элементов: школы, вуза и министерства, которые оказывают существенное влияние на организацию учебного процесса (понятно, что число элементов, входящих в приведенную структурную модель, может быть гораздо больше).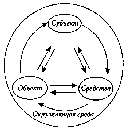


Рис 3.8. Полная формальная модель деятельности человека
Однако при декомпозиции необходимо учитывать и другой критерий - простоту, который требует сокращения размеров древовидной структуры. Таким образом, при декомпозиции должен быть принят некий компромисс между полнотой и простотой, который может быть достигнут в том случае, если в структурную модель включаются только элементы, существенные по отношению к цели анализа.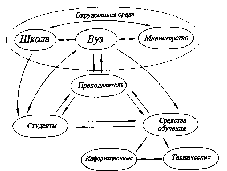


Рис 3.9. Формальная модель педагогического процесса в вузе
Число уровней декомпозиции (уровней древовидной структуры) выбирается из следующих соображений. Декомпозиция по каждой из ветвей древовидной структуры ведется до тех пор, пока не приведет к получению элементов системы, не требующих дальнейшего разложения. Такие составляющие называются элементарными. Отметим, что понятие элементарности составляющей системы должно быть конкретизировано в каждом рассматриваемом случае отдельно. При этом могут быть использованы как формализованные (с помощью критериев), так и неформализованные (с помощью экспертов) способы. Например, в некоторых случаях многомерную задачу механики сплошной среды удается разложить на последовательность одномерных задач, имеющих простое (аналитическое) решение. Тогда каждую из этих одномерных задач можно считать элементарной частью исходной системы.

Часть системы, которую нельзя считать элементарной на основании выбранных критериев, подлежит дальнейшей декомпозиции. При этом могут использоваться различные фреймы. Если исследователь «перебрал» все фреймы, но не достиг элементарности на какой-либо ветви древовидной структуры, то вводятся новые элементы в модель, взятую в качестве основания, и декомпозиция продолжается по ним.

Следует отметить, что в результате декомпозиции будет реализован лишь первый этап структурного моделирования, а именно - этап анализа. После этого этапа удается разделить исследуемую систему на отдельные элементы (или исходную задачу - на более простые подзадачи). Однако, как было отмечено выше, на поведение каждого элемента нужно смотреть с точки зрения целей всей системы. Другими словами, полученная совокупность элементов кроме внешней целостности (т.е. определенной обособленности от окружающей среды) должна обладать и внутренней целостностью.

Внешняя целостность хорошо описывается моделью «черного ящика», а внутренняя - связана с моделью структуры системы, т.е. установлением отношений между элементами. Для этого используется операция агрегирования - объединение нескольких элементов в единое целое. Результатом агрегирования является система, которую называют агрегатом. Свойства агрегата не являются только совокупностью свойств его отдельных элементов. Агрегат может обладать такими свойствами, которых нет ни у одного из его элементов, взятых в отдельности. Другими словами, объединение элементов в систему влечет появление нового качества, которое не могло появиться без этого объединения. Такое «внезапное» появление новых качеств у агрегата получило название эмерджентности (от англ. – внезапно возникающий). Следует отметить, что новые свойства возникают благодаря конкретным связям между элементами. Другие связи могут дать другие новые свойства агрегата.

Хорошей иллюстрацией свойства эмерджентности является пример, предложенный М. Арбибом. Пусть имеется некоторый цифровой автомат 5, увеличивающий на 1 любое целое число, поступающее на его вход. При последовательном соединении двух автоматов в цепочку это свойство не изменяется. Если же соединить два таких автомата последовательно в кольцо (рис. 3.10), то в полученном агрегате обнаружится новое свойство: он генерирует возрастающие последовательности на выходах А и В, причем одна последовательность состоит из четных, а другая – из нечетных чисел. Другим ярким подтверждением свойства эмерджентности может служить пример из материаловедения. Известно, что тип кристаллической решетки (способ соединения атомов) определяет твердость материала. При этом твердость получаемого агрегата, состоящего из одинаковых элементов, может различаться в десятки тысяч раз (графит и алмаз).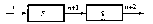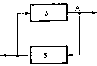




Рис. 3.10. Пример вычислительного агрегата
Возникновение качественно новых свойств при агрегировании есть частное, но яркое проявление одного из законов диалектики - закона перехода количества в качество. При этом считается, что чем больше свойства агрегата отличаются от свойств его элементов, тем выше организованность системы. Кибернетик У. Эшби доказал, что у системы тем больше возможностей в выборе поведения, чем сильнее степень согласованности поведения ее элементов. Высшая степень проявления согласованности поведения элементов системы – самоорганизация системы, изучением которой занимается относительно молодая междисциплинарная область знаний – синергетика.

Таким образом, как следует из вышеизложенного, при агрегировании большое значение имеет установление связей между элементами, т.е. выбор модели структуры. Значит, в самом общем виде агрегирование можно определить как установление отношений на заданном множестве элементов. Такое установление отношений может быть проведено различными способами: построением математических зависимостей, структурированием, статистической обработкой, классификацией и т.п. В результате получаются различные агрегаты, основными из которых являются следующие: конфигуратор, классификатор, оператор, статистик и структура. Рассмотрим эти агрегаты более подробно.

Конфигуратором называется такой агрегат, который состоит из качественно различных языков описания исследуемого объекта и обладает тем свойством, что число этих языков минимально, но необходимо для выполнения заданной цели. Следует отметить, что конфигуратор является содержательной моделью высшего возможного уровня. Перечислив языки, на которых будет вестись описание системы, мы тем самым определяем тип системы и ее основные свойства.

Например, в радиотехнике для описания одного и того же прибора используется следующий конфигуратор: блок-схема, принципиальная схема и монтажная схема. Этот конфигуратор полностью описывает рабочие характеристики прибора. Однако если кроме цели производства радиоаппаратуры ставится цель ее сбыта, то в конфигуратор необходимо добавить язык рекламы (маркетинг, дизайн, цена и т.п.).

В инженерной графике для описания поверхности любого трехмерного тела в качестве конфигуратора используются совокупность трех ортогональных проекций. Число их нельзя уменьшить и нецелесообразно увеличивать.

А какой конфигуратор применяется при математическом моделировании? Выбор языка зависит от вида модели. Понятно, что основной язык для математической модели – язык математических формул. Однако, как было отмечено выше, важными этапами математического моделирования являются содержательная и концептуальная постановки задачи. На этапе содержательной постановки осуществляется словесная постановка задачи на том языке, на котором она формулируется заказчиком. На этапе концептуальной постановки выполняется запись задачи на языке тех областей знаний, которые используются при моделировании рассматриваемого объекта. Поэтому конфигуратором в данном случае можно считать содержательную, концептуальную и математическую постановки задачи.

В качестве классификатора выступает агрегат, устанавливающий отношения эквивалентности между элементами системы, т.е. описывающий условия образования классов.

Следующим типом агрегата является оператор, который ставит в соответствие некоторому набору отдельных элементов один элемент.

Наиболее распространенный в математическом моделировании вид оператора – функция. Этот вид оператора появляется, если агрегируемые элементы измеряются в числовых шкалах. В таком случае можно задать отношение на множестве элементов в виде числовой функции многих переменных, которая и является агрегатом.

Приведенный вид функции - один из простейших. В общем случае области определения и значений функции могут относится к более сложным пространствам и множествам. Конкретное задание функции связано с построением математической модели рассматриваемой системы. Поэтому на выбор функции накладываются ограничения, вытекающие из содержательной постановки задачи, т.е. этот выбор не является свободным. В тех же (достаточно редких) случаях, когда оператор-функция является вполне адекватной математической моделью всей системы, свобода выбора функции, агрегирующей набор внутренних переменных, вообще отсутствует. Такой случай имеет место, например, когда закономерности природы удается с достаточной степенью адекватности отобразить безразмерными степенными одночленами физических размерных величин. При этом можно утверждать, что если удалось построить безразмерный степенной одночлен из размерных физических величин, образующих конфигуратор определенного явления, то установлен физический закон данного явления. Это легко можно показать на примере второго закона Ньютона, описывающего поступательное движение твердого тела.

К сожалению, построить функциональную зависимость, адекватно описывающую поведение сложной системы, очень трудно, а иногда практически невозможно. Гораздо проще установить функциональные зависимости между отдельными элементами системы. В этом случае оператор будет представлять собой некоторую (часто нелинейную) систему уравнений. Как правило, внутренними переменными системы являются не числа, а функции одного или нескольких аргументов. Тогда выходными параметрами могут выступать также функции, или функционалы.

При математическом моделировании сложных систем построить оператор бывает совсем не просто. Это связано со многими причинами. Основной из этих причин можно считать недостаток информации о характере и механизмах взаимодействия между отдельными элементами системы. Например, эти взаимодействия могут носить случайный характер, закон которого нам неизвестен. В этом случае говорят, что моделирование ведется в условиях неопределенности, а оператор/может быть найден только с некоторой ограниченной точностью, например с точностью до конечного числа параметров.

Обычно считается, что параметры носят случайный характер или могут быть определены в ходе самого моделирования с помощью методов идентификации. В этом случае используются системы с обратной связью. Назовем оператор, который задается с помощью алгоритма, реализующего некоторый набор правил, имитатором.

Отдельно при агрегировании рассматривается ситуация, когда все параметры, описывающие поведение элементов системы, являются случайными величинами. В этом случае вводится понятие агрегата-статистика, определяющего отношения на множестве случайных параметров системы. Для его построения используются функции выборочных значений случайных величин, в качестве которых широко используются функции распределения вероятностей или плотности распределения вероятностей случайных событий.

На практике используются достаточные и оптимальные статистики. Достаточными статистиками называются такие агрегаты, которые извлекают всю полезную информацию об интересующем нас параметре из совокупности наблюдений. Например, для систем, результат деятельности которых нас интересует только в среднем, достаточным статистиком может служить математическое ожидание выходной случайной величины. Однако на практике достаточные статистики применяются редко, так как при таком агрегировании потери информации неизбежны. Чаще применяются оптимальные статистики – такие агрегаты, которые позволяют свести потери информации к минимуму. Например, математическое ожидание и дисперсия случайной величины в совокупности являются оптимальным статистиком для многих технических систем.

Последним из рассматриваемых видов агрегатов, но не последним по частоте применения при структурном моделировании является структура системы, т.е. агрегат, устанавливающий типы связей между отдельными элементами системы. Наиболее широко подобный вид агрегирования применяется при моделировании технических, информационных и организационных систем. Например, в материаловедении в качестве структуры материала используются разные модели кристаллических решеток, устанавливающие типы связи между атомами и симметрийные свойства кристалла. В информационных системах применяется структура в виде первичной сети, указывающей направление и интенсивность передачи информации. В организационных системах структура описывает иерархию в процессе принятия решений и распределение власти и ответственности (ответственность за принятые решения).

После рассмотрения основных подходов к построению структурных моделей перейдем к примерам, иллюстрирующим эффективность этих подходов при моделировании различных систем и процессов.

3.3. Вопросы для самопроверки

Что такое искусственная система? В каком случае совокупность от дельных элементов будет системой, а в каком - нет? Приведите примеры.

Когда на практике можно применять модель «черного ящика»? Какие основные недостатки имеет данная модель?

В чем сложность построения модели «белого ящика»? Какие виды неопределенностей вы знаете?

Что такое структурная схема системы? Чем отличается граф от сети?

В чем заключается основная особенность иерархических структурных схем? Где применяются иерархические структуры?

Почему синтез считают завершающим этапом анализа?

Что такое фрейм? Является он формальной или содержательной структурной моделью?

Сформулируйте условия окончания декомпозиции системы.

Что такое агрегат? Может ли агрегат обладать новыми свойствами по сравнению с теми, которыми обладают составляющие его элементы?

Какой агрегат называется оператором? Переменные и параметры оператора. Какие виды неопределенности оператора вы знаете?

Постройте структурную модель системы управления, которая реализована в вашем учебном заведении.

Постройте структурную модель спортивной команды (например, хоккейной или футбольной).

Постройте структурную модель автомобиля.

Постройте структурную модель солнечной системы.

Постройте агрегат-классификатор численных методов решения систем алгебраических уравнений.

Постройте одномерную структурную модель упрочняющегося упругопластического тела, для которого задана диаграмма приведенного вида. Постройте определяющие соотношения, соответствующие вашей структурной модели.