Лекции по статистике [Фляжникова]. Конспект лекций Дисциплина Статистика
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
|
Тема 4. Статистические таблицы и графики 1. Статистические таблицы Таблица – это форма наиболее рационального изложения цифрового материала. Основа (остов) статистической таблицы - это ряд взаимопересекающихся горизонтальных и вертикальных линий, образующих по горизонтали строки, а по вертикали графи (столбцы). Каждая строка и графа имеет свое наименование, которая должна соответствовать содержанию таблицы. Таблица должна иметь указания, что это таблица и название, определяющее ее содержание. В таблице есть подле6жщее и сказуемое. Подлежащим таблица называется объект, который в ней характеризуется цифрами, сказуемое таблицы образует система показателей, которыми характеризуется объект изучения, т.е. подлежащее таблицы. Виды таблиц. 1. Простые таблицы – это те таблицы, в подлежащем которых нет группировок. Они бывают перечневые, хронологические и территориальные; 2. Групповые таблицы. В них объект разделен на группы по тому или иному признаку; 3. Комбинационные таблицы. В них объект разделен на группы по двум и более признакам, взятым в комбин6ации 2. Графики и их виды Графиком называют наглядное изображение статистических величин при помощи геометрических линий и фигур или географических картосхем (картограмм). В каждом графике существуют основные элементы: 1. графический образ (основа графика) – это геометрические знаки, совокупность точек, линий, фигур, с помощью которых изображаются статистические величины; 2. поле графика – это то место, где расположены графические образы; 3. пространственные ориентиры, определяющие размещение геометрических знаков на поле; 4. масштабные ориентиры, дающие этим знакам количественную определенность; 5. экспликация графика, включающая в себя его название и соответствующие пояснения отдельных его частей. Масштабные ориентиры определяются системой масштабных шкал. Масштабом графика называется условная мера перевода числовой величины в графическую. Масштабная шкала – это линия, отдельные точки которой могут быть в соответствии с принятым масштабом прочитаны как определенное значение статистического показателя. Виды статистических графиков. Статистические графики классифицируются с разных точек зрения. Мы уже приводили их классификацию по характеру применяемых графических образов. С точки зрения разрешаемых задач статистические графики можно разделить на 1) графики сравнения статистических показателей; 2) графики структуры и структурных сдвигов; 3) графики динамики; 4) графики контроля выполнения плана; 5) графики пространственного размещения и пространственной распространенности (картограммы и картодиаграммы); 6) графики вариационных рядов; 7) графики зависимости варьирующих признаков. Тема 5. Абсолютные и относительные величины. 1. Абсолютные величины. В итоге статистической сводки образуются обобщающие показатели, характеризующие результаты познания количественной стороны общественных явлений. К таким показателям относят абсолютные, относительные и средние величины. Абсолютные величины бывают двух видов индивидуальные; суммарные. Индивидуальные характеризуют размеры отдельных единиц совокупности. Индивидуальные абсолютные величины получают в результате статистического наблюдения и фиксируют в первичных документах. Суммарные абсолютные величины определяют путем суммирования отдельных индивидуальных величин. Абсолютные величины отражают естественную основу явлений, они выражаются либо численностью единиц совокупности, либо в их абсолютных размерах в натуральных единицах, вытекающих из физических свойств. Абсолютные величины измеряются в следующих единицах измерения: натуральных (тонны, кг., гр., шт.); в трудовых (часы, дни, месяца, человеко-часы, человеко-дни); стоимостные (руб., млн. руб.); комбинированные (тон. км., цент/га.). При определении суммарных показателей, когда индивидуальные величины характеризуют отдельные разновидности продукции, близкие по своим свойствам, применяются условные натуральные измерители. При определении абсолютных показателей их могут сравнивать, при этом рассчитывая абсолютные отклонения. Пример. Стоимость основных фондов тыс. руб.
По данным таблицы можно сделать вывод, что стоимость О.Ф. на конец года увеличилась на 45 тысяч рублей. 2. Относительные величины. Одной из наиболее распространенных обобщающих величин в статистике является относительная величина. Относительные величины представляют собой меру количественного соотношения конкретных явлений в общественной жизни. Относительная величина рассчитывается как отношение двух взаимосвязанных показателей. При этом в числителе находится сравниваемая величина, а знаменатель содержит базу относительного сравнения. Если база сравнения принята за единицу, то рассчитываемый показатель называется коэффициент. Если база сравнения принята за сто, то называется процент. Если база принимается за тысячу, то исчисляемая величина называется промилей. Если за десять тысяч, то продецемилей. Относительные величины бывают следующих видов: Процент выполнения плана: факт/план Относительная величина структуры – характеризует долю отдельных частей в общей совокупности. Относительные величины структуры называют удельным весом единиц в общей совокупности.
3. Относительные величины динамики, они характеризуют изменения явлений во времени по сравнению с уровнем, принятым за базу сравнения. Пример. у0 у1 у2 у3 у4
Относительные величины динамики принято называть темпами роста (Т). Цепные темпы роста Базисные темпы роста - за основу принимается постоянная база сравнения, т.е. начальный уровень ряда динамики. Относительные величины координации, характеризующие отношения отдельных частей совокупности с одной из них, принятой за базу сравнения (численность сел. жителей на 100 человек городских жителей). Относительные величины интенсивности – показатели, характеризующие меру распространения или развития данного явления в определенной среде, они рассчитываются как отношение абсолютной величины к размеру среды, в которой они находятся (производство сельскохозяйственной продукции с 1 га сельскохозяйственных угодий; фонд отдачи, т.е. сколько рублей товарной продукции получено на 1 рубль вложенные в основные средства). Относительные величины сравнения, получаются путем сравнения одноименных уровней, относящихся к разным объектам, территориям за один и тот же период или на один и тот же момент времени (производство хлеба на вяземском заводе по сравнению с сафоновским). Тема 6. Средние величины и Показатели вариации 1. Сущность средних величин и их значение в статистическом анализе. Средней величиной является обобщающая характеристика большого количества индивидуальных значений варьирующего признака. Средняя величина – то общее, что характерно для всей совокупности, но исключает те отличия, которые наблюдаются у отдельных единиц как бы взаимно погашая их. Средние величины должны определятся не для всех совокупностей, а только для тех, которые являются однородными. Средние величины, полученные для неоднородных совокупностей не только не имеют ценностей, но даже могут принести вред искажая истинный характер общественного явления. Таким образом, в статистике средней величиной является обобщающий показателей, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности. Значение средней величины в следующем: их используют для оценки результатов использования научных разработок в производстве, в социальной жизни, а также в изыскании скрытых и неиспользованных резервов. 2. Виды средних величин. 1. Средняя арифметическая величина. Самым распространенным видом расчета средней величины является определение средней арифметической. Пример. 5 рабочих токарей делают одинаковые детали за смену: первый – 12 второй – 9 третий – 11 четвертый – 13 пятый – 15 Определить среднюю производительность. Всего – 60. Производительность – 12= 60/5 В этом случае производятся вычисления по формуле средней арифметической простой где х – варианта; n – число единиц совокупности несгруппированного ряда. Данная формула применяется в том случае, если в исходных данных значение каждого варианта встречается один раз. Если же значение вариант (х) встречается по несколько раз, т.е. имеет место частота, то расчет средней арифметической производится по формуле средней арифметической взвешенной где х – варианта; Пример. Определить среднюю грузоподъемность одного крана, если имеется:
Средние арифметические применяются в тех случаях, когда общий объем варьирующего признака для всей совокупности образуется как сумма значений признаков отдельных ее единиц. При расчетах средней арифметической выделяются ее основные свойства: - среднее от постоянной величины равна ей самой: произведение средней на сумму частот равно сумме произведений вариант на частоты: изменение каждого варианта на одну и туже величину изменяет среднюю величину на эту же величину: изменение каждого варианта на одно и тоже число изменяет среднюю во столько же раз: изменение каждой частоты в одно и тоже число раз не изменяет величину средней: алгебраическая сумма отклонений всех вариантов от средней равна 0: Определение средней арифметической по данным интервального вариационного ряда происходит следующим образом, – для каждого ряда определяется среднее значение интервала как полусумма его нижнего и верхнего значения вариант, а далее расчет ведется по формуле средней арифметической взвешенной. Пример. Распределение рабочих цеха по производительности
2. Средняя гармоническая величина. Это величина обратная среднеарифметической. Она применяется, когда известны отдельные значения варьирующего признака и вся совокупность признаков, а частоты неизвестны. Существует два вида среднегармонической: Средняя гармоническая простая определяется: 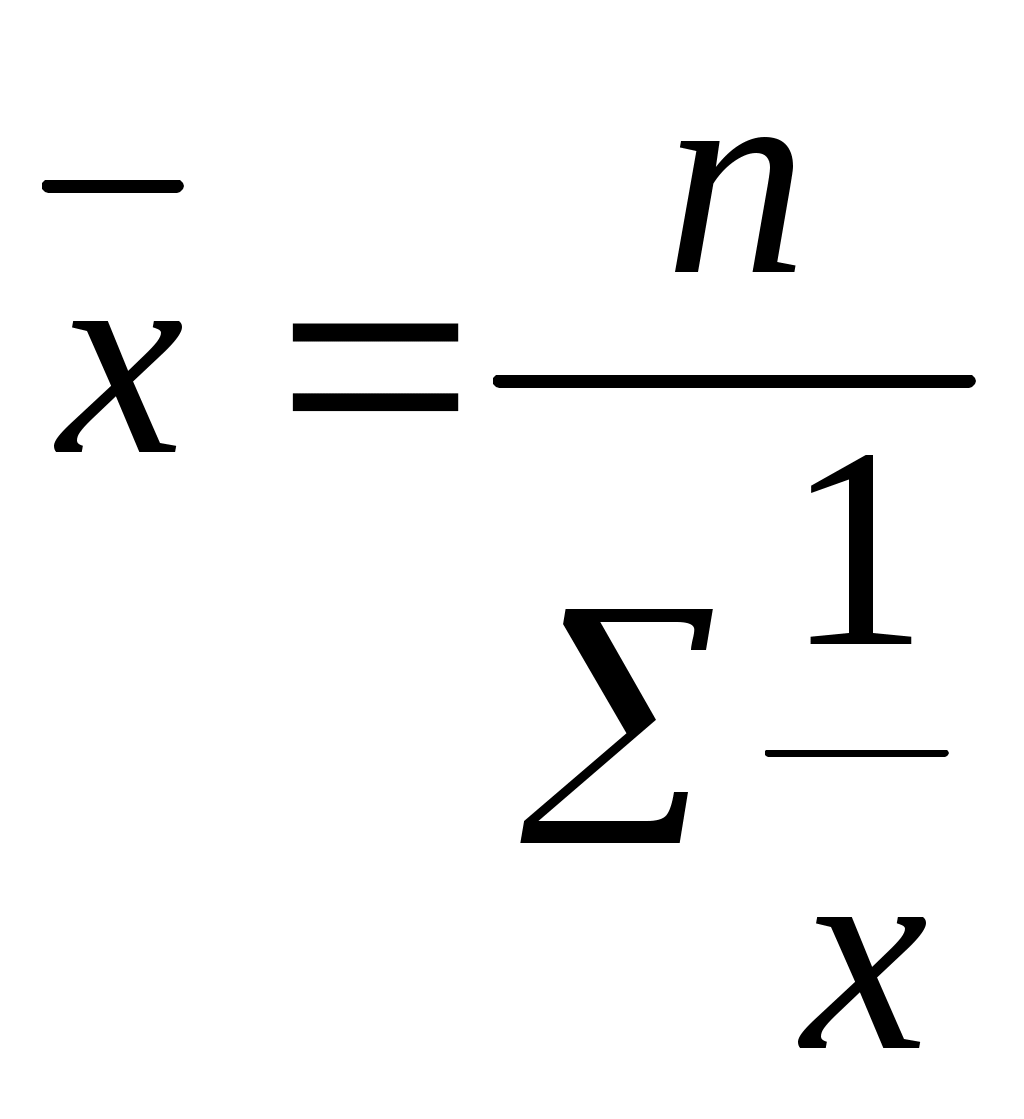 где n – число единиц совокупности для несгруппированного ряда; Пример. Скорость по течению реки 60 км/ч., против течения – 40 км/ч. Определить среднюю скорость движения. Весь путь S=1, но тем не менее путь проходят дважды, то S=2, V1=60 км/ч., V2=40 км/ч., тогда средняя скорость движения: 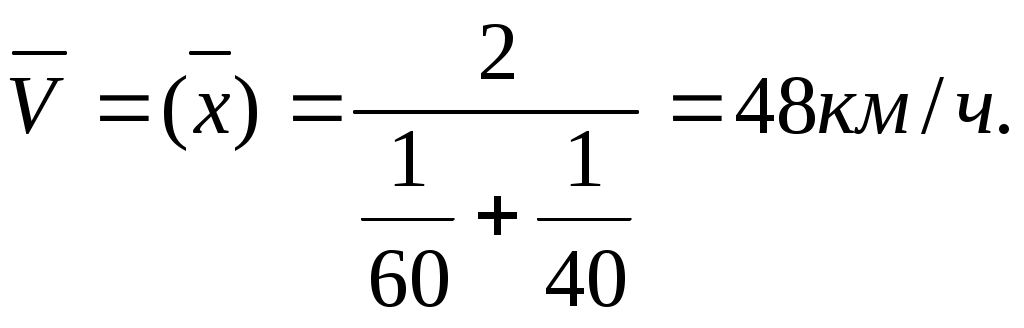 Средняя гармоническая взвешенная определяется: 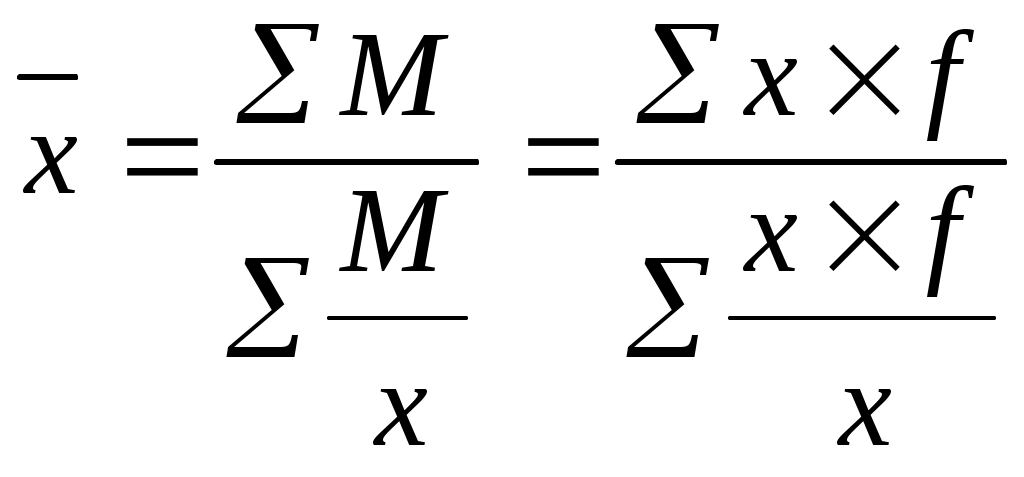 Пример. Имеются данные о валовом сборе и урожайности зерновых культур по трем колхозам:
Определить среднюю урожайность. Валовый сбор = урожайность Частота – площадь посевов 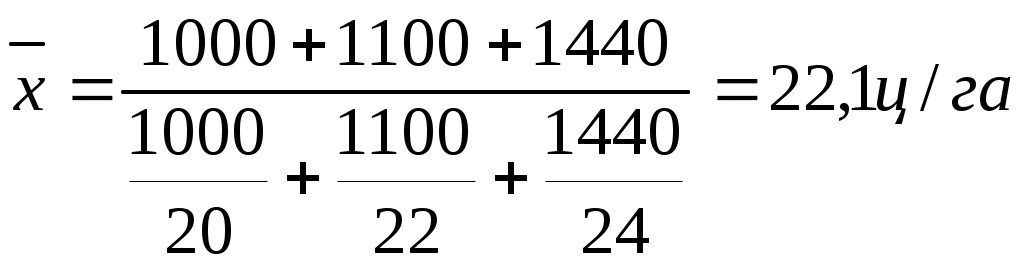 3. Средняя хронологическая величина. Применяется для определения среднего уровня в моментных рядах динамики. Существует два вида рядов динамики: моментные; интервальные. Интервальные – это такие ряды в которых данные приводятся за определенный период времени (месяц, год). Средний уровень ряда в интервальном ряду определяется по средней арифметической простой. Моментные – это такие ряды, где данные представлены на определенный момент времени (на определенную дату). Если интервалы времени между датами равны, то расчет средней ведут по формуле средней хронологической простой. Пример. Моментный ряд:
Если интервалы между датами в моментных рядах не одинаковые, то расчет ведется в два этапа: по средней хронологической взвешенной определяется средняя внутри каждого интервала времени по среднеарифметической простой; определяется общая средняя по среднеарифметической взвешенной, где частотами являются интервалы между датами. Пример. Имеются данные о численности населения города на: – 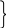 632 тыс. чел., 632 тыс. чел.,1 год – 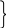 645 тыс. чел., 645 тыс. чел.,4 .5 года 1 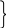 .07.98 – 649 тыс. чел., .07.98 – 649 тыс. чел.,0.5 года 1.01.99 – 657 тыс. чел. Определить среднюю численность: где 2 – это два полугодия; 1 – это одно. 4. Средняя квадратическая величина. Применяется при определении показателей вариации и рассчитывается как корень квадратный из средней арифметической. Средняя квадратическая простая: Взвешенные: 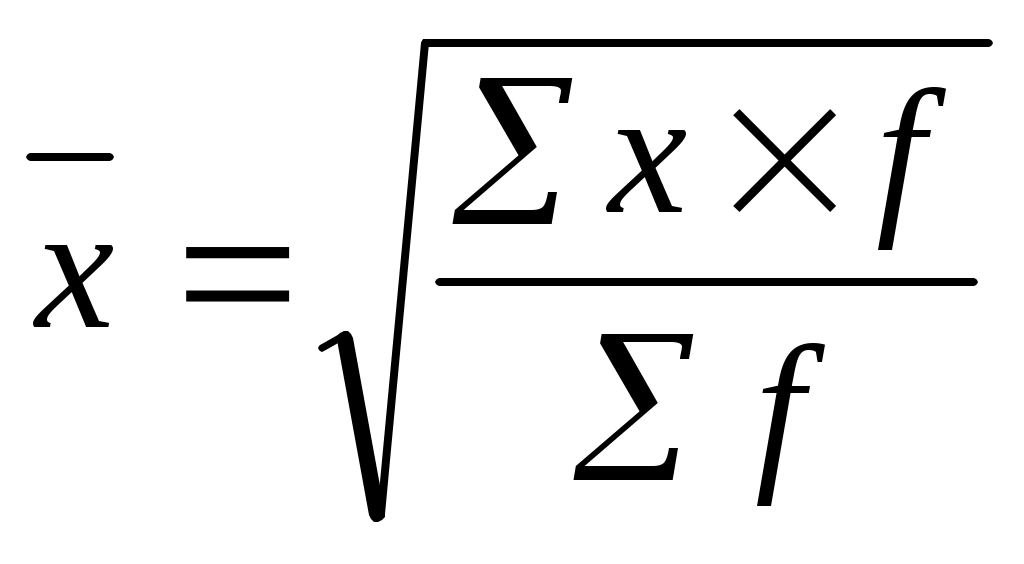 5. Средние структурные величины. При определении среднеструктурных величин определяются мода и медиана. Медиана – вариант, расположенный в центре ранжированного ряда, медиана делит ряд на две одинаковые части, таким образом, чтобы по обе ее стороны находилось одинаковое число единиц совокупности. Если всем единицам ряда придать порядковые номера, то порядковый номер медианы будет определяться по формуле Нахождение медианы в интервальных вариационных рядах требует предварительного определения интервала в котором находится медиана, т.е. медианногоинтервала – этот интервал характеризуется тем, что его коммулятивная частота равна полусумме или превышает полусумму всех частот ряда. В зависимости от этого медиану определяют по формуле: 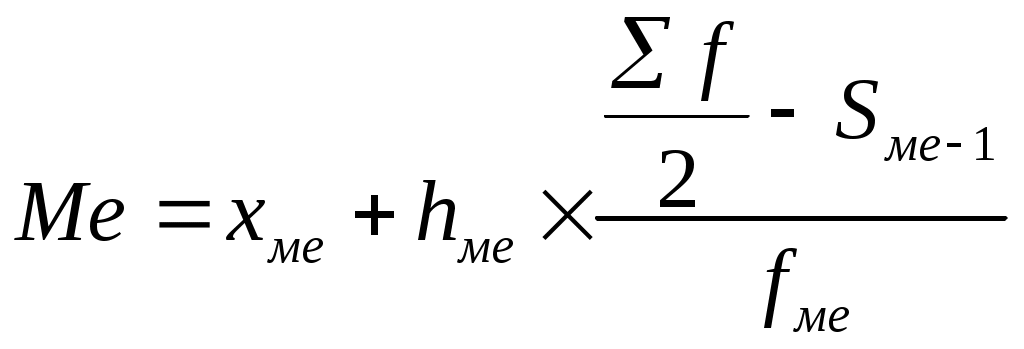 где Пример. Определить медиану, если:
Вывод: из 1000 рабочих 500 чел. имеет стаж работы меньше 8,57.лет. Квартиль –это четвертая часть совокупности, определяется как и медиана, только сумму частот необходимо разделить на 4, а при определении квартильного интервала коммулятивная частота должна быть больше или равна четверти суммы частот совокупности. Мода – вариант наиболее часто встречающийся в совокупности. В дискретном ряду мода – это вариант с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант модального интервала. В пределах интервала надо определить то значение признака, который обладает наибольшей частотой. Определяем по формуле: где Дециль – делит совокупность на десять равных частей. Определяется аналогично как и квартиль только сумму частот необходимо разделить на 10. Средняя геометрическая. Применяетсядля характеристики рядов динамики при определении средних темпов роста. Пример. Определить цепные темпы роста и средний темп роста товарной продукции, если:
средний темп роста = | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
