Лекции по статистике [Фляжникова]. Конспект лекций Дисциплина Статистика
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
|
Тема 10. Индексы 1. Общие понятия об индексах. Для характеристики явлений и процессов экономической жизни, статистика наряду с другими показателями использует индексы. Слово «индекс» в переводе – показатель. Индекс – обобщающий показатель сравнения двух совокупностей, состоящих из элементов, которые непосредственно не подчиняются суммированию. К совокупностям, элементы которых можно суммировать, относятся те совокупности, в которых дается сравнительная характеристика объемов: динамика посевных площадей, динамики выпуска конкретного вида продукции, динамики оплаты труда и т.д. К совокупностям, элементы которых не поддаются суммированию, относятся такие 2 вида: - характеристика 1 тонны пшеницы, молока, стали и т.д. В таких совокупностях рассчитывается индекс физического объема произведенной (проданной, потребленной) продукции; - совокупности, где характеризуются цены (одной тонны пшеницы, молока и т.д.). Для характеристики общего уровня цен (себестоимости, производительности, урожайности)применяются индексы себестоимости, цен и т.д. Индексы применяются в следующих сферах: 1). Для сравнительной характеристики элементов конкретной совокупности; 2). Динамики; 3). Для пространственного сравнения; 4). Для сравнения факта с планом; 5). При факторном анализе. 2. Классификация индексов. Индексы классифицируются по ряду признаков: 1. В зависимости от объектов исследования: индексы объема (структуры); качественные индексы (индексы цены, себестоимости). 2. По охвату: индивидуальные индексы; общие индексы; групповые индексы. Индивидуальные индексы – дают сравнительную характеристику отдельных элементов совокупности (индекс физического объема, себестоимости, производительности и т.д.). Обозначается i. Общие индексы – характеризуют изменение совокупности в целом, обозначают J. Групповые индексы – охватывают не все элементы совокупности, а только отдельные части. Групповые индексы рассчитывают с помощью метода группировок, собирая и группируя данные за период. 3. В зависимости от методологии расчета общие и групповые индексы делят на: агрегатные; средние из индивидуальных. Агрегатные – основная форма экономических индексов. Средние из индивидуальных – производная форма, они получаются путем расчета и преобразования агрегатных. Если совокупность состоит из 3 и более периодов, то может быть рассчитана цепная и базисная система индексов. 3. Принципы и методы исчисления общих индексов. Для того, чтобы рассчитать общий индекс, необходимо преодолеть несуммарность отдельных элементов изучаемого явления, это достигается путем введения в индекс дополнительного неизменного показателя, тесно связанного с индексируемой величиной. Этот показатель называется весами агрегатного индекса или показателем сопряжения. Так, если индексируются цены, то для того, чтобы преодолеть несуммарность цен, цены умножают на количество. Существует два правила построения общих индексов: 1. Если строятся индексы объема (структуры), то качественные величины берутся по базисным данным. 2. Если строятся индексы качества, то объемные величины берутся по отчетным данным. Агрегатные индексы В международной статистике для построения агрегатных индексов применяются следующие обозначения: q – физический объем произведенной продукции (количество); p – цена; z – себестоимость; d – структура (удельный вес); 1 – отчетный период; 0 – базисный период. Пример.
Индивидуальный индекс физического объема проданной продукции определяется путем деления конкретного элемента совокупности в отчетном периоде на базисный период: Общий индекс физического объема определяется по формуле: где Индекс физического объема показывает, что за счет изменения количества реализованной продукции изменяется размер товарооборота в отчетном периоде по сравнению с базисным. Товарооборот возрос на 24%. Для того, чтобы определить изменение товарооборота в натуральном выражении , необходимо из числителя общего индекса физического объема вычесть знаменатель: Индекс цены Общий индекс цены показывает на сколько % изменился размер товарооборота в отчетном периоде по сравнению с базисным за счет изменения индивидуальных цен. Для того, чтобы рассчитать на сколько рублей изменился товарооборот за счет изменения цен нужно применить формулу: Вывод: общий индекс цены показывает, что на 6,96 % уменьшился размер товарооборота за счет изменения цен. Общий индекс товарооборота Общий индекс товарооборота показывает на сколько % изменяется товарооборот в отчетном периоде по сравнению с базисным при влиянии двух факторов и цены и физического объема. Для того, чтобы узнать на сколько рублей изменился товарооборот в отчетном по сравнению с базисным периоде, необходимо из числителя вычесть знаменатель: 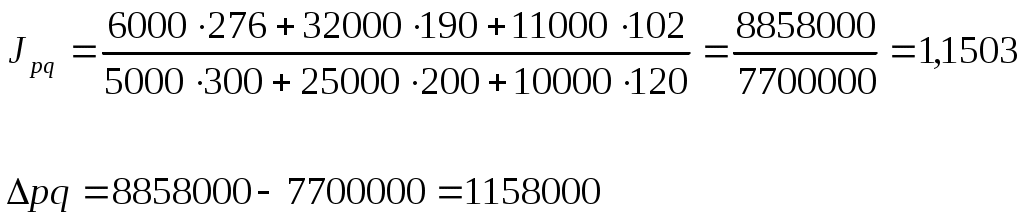 Вывод: товарооборот в августе увеличился по сравнению с июлем на 15 %. Между индексом цены, индексом физического объема и индексом товарооборота существует взаимосвязь: 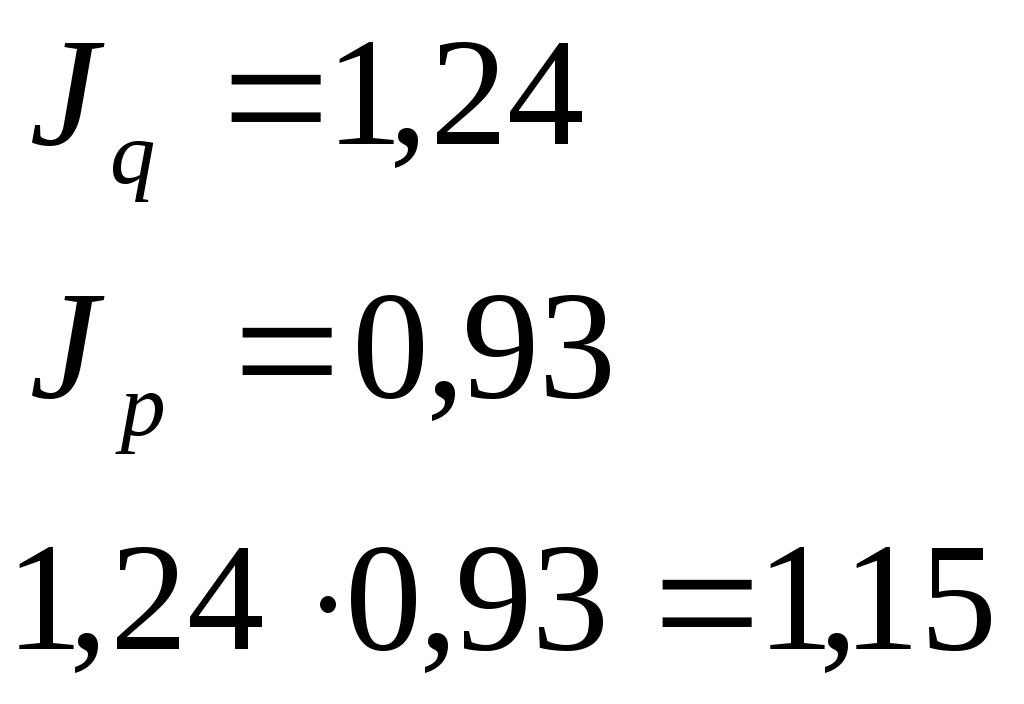 Индексы постоянного, переменного состава и индексы структурных сдвигов Индекс постоянного состава показывает изменение общей средней цены за счет изменения индивидуальных цен в отчетном периоде по сравнению с базисным. Индекс структурных сдвигов показывает изменение средней цены в отчетном периоде за счет изменения физического объема. Индекс переменного состава – это индекс средней цены, который показывает на сколько % средняя цена изменяется в отчетном периоде по сравнению с базисным. Индекс переменного состава равен произведению индекса постоянного состава на индекс структурных сдвигов: 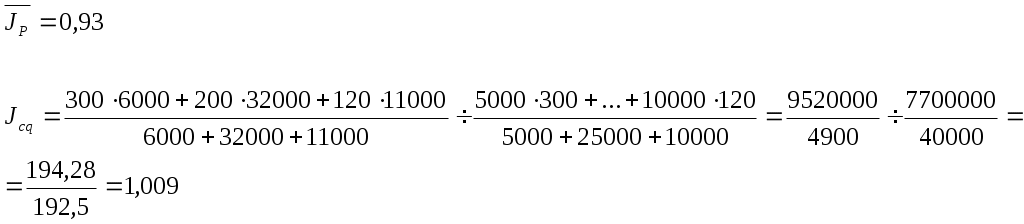 Средние индексы Для характеристики обобщающих показателей, характеризующих изменение количественной характеристики явления, используются средние индексы. На основе агрегатных индексов могут быть рассчитаны: средний арифметический индекс; средний гармонический индекс. Средний арифметический индекс вычисляется при исчислении индивидуального индекса физического объема. Он используется, если неизвестны данные о физическом объеме в отчетном периоде, в таком случае физический объем отчетного периода рассчитывают исходя из индивидуального индекса физического объема: 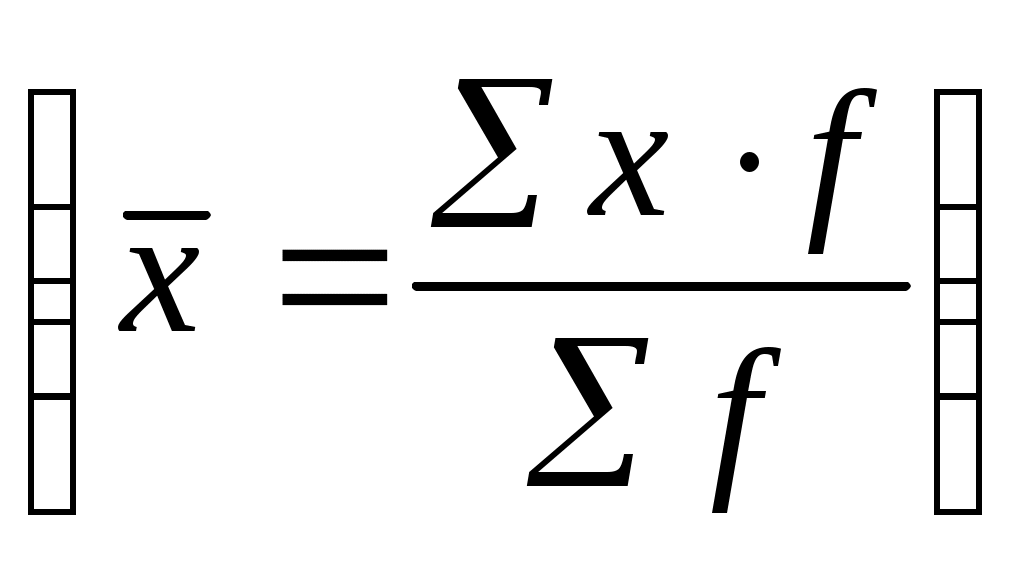 Индекс средний арифметический вычисляется: Средний гармонический индекс определяется исходя из преобразований агрегатного индекса цены, для этого, исходя из расчета индивидуального индекса цены, определяется цена базисного периода. Средний гармонический индекс цены вычисляется: 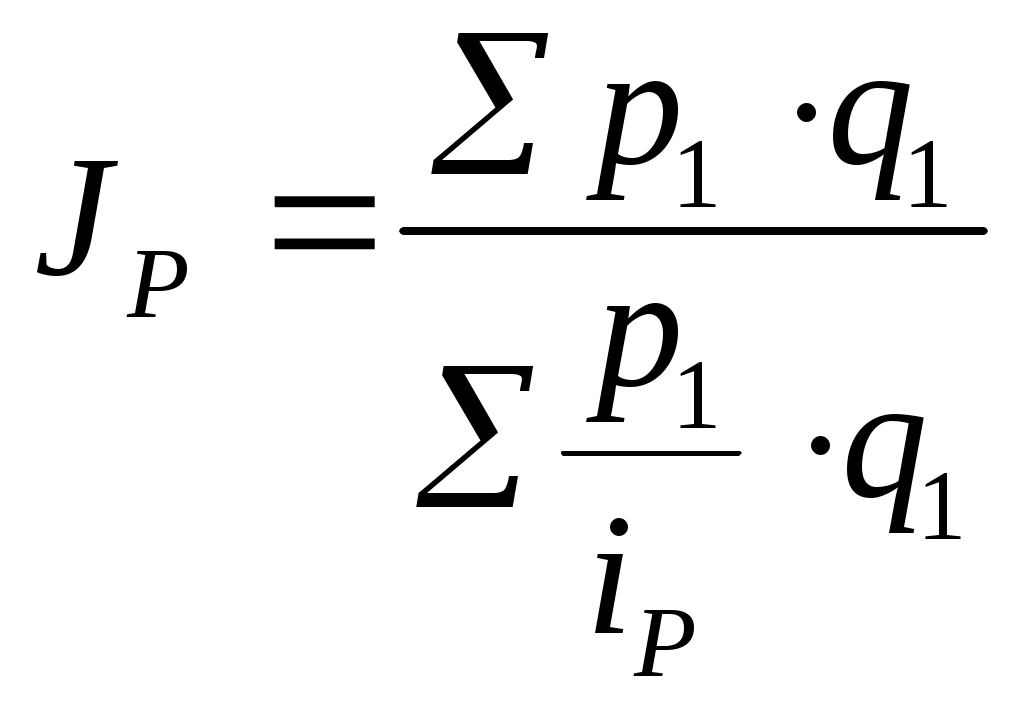 Пример. Используя следующие данные о производстве продукции на хлебозаводе, определить общий рост физического объема в отчетном периоде по сравнению с базисным, используя взаимосвязь индексов, определить на сколько % изменились цены, если известно, что стоимость хлеба в фактических ценах выросла на 2 %.
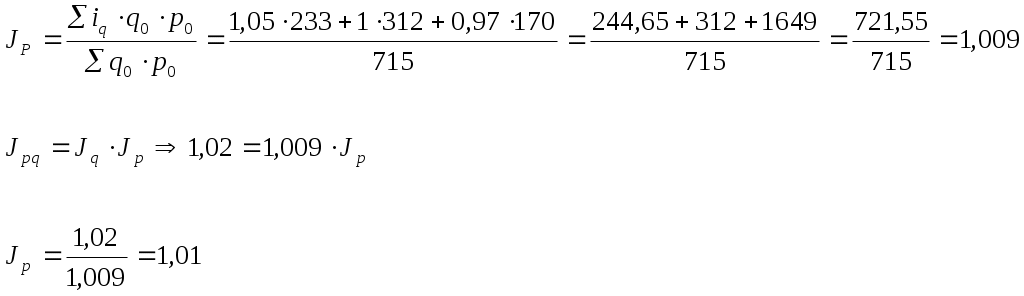 4. Индексный метод анализа факторов Индексный метод широко применяется для анализа роли отдельных факторов в динамике социально-экономического явления. Изменение количественной характеристики данного явления происходит под влиянием одного или нескольких факторов, выступающих как множителей совокупного результата. Пример, динамика товарооборота в фактических ценах обусловлена совместным изменением как цены, так и количества проданных товаров. Индекс физического объема товарооборота и индекс цены выступают соизмерителями роли этих факторов на общее изменение размера товарооборота в фактических ценах. Таким образом, чтобы образовать систему индексов, необходимо чтобы соизмерителями в индексах были разные уровни, причем это соизмерение получалось через произведение двух или нескольких индексов. Тема 11. Статистические методы изучения взаимосвязей между социально-экономическими явлениями и процессами. 1. Взаимосвязи общественных явлений и необходимость их статистического изучения. Общественные явления формируются под действием многих факторов. В соответствии с принципом диалектического материализма общественные явления органически связаны между собой, зависят друг от друга, обуславливают друг друга и находятся в постоянном движении и развитии. Поэтому изучить то или иное явление можно только на основе взаимосвязи с окружающими его явлениями. Связь между общественными явлениями многообразна (связь между производством, потреблением, распределением продукции). Одной из основных задач экономической реформы является: повышение эффективности производства. Решению этой задачи призван способствовать научно обоснованный экономический анализ, в котором повышается роль и значение статистического метода выявления взаимосвязей. 2. Виды и формы взаимосвязей между явлениями. Существует два вида связи между факторами и результативными признаками: функциональная связь корреляционная связь При функциональной связи каждому значению величины факторного признака соответствует только одно значение результативного признака. Функциональные связи обычно выражаются формулами и исследуются в математике и физике. Пример, площадь круга – результативный признак – прямо пропорциональна его радиусу – факторный признак. Однако, функциональные связи имеют место и в экономике. Пример, заработная плата рабочего повременной оплате равна произведению часовой тарифной ставки на число отработанных часов. Функциональная связь является точной и полной, т.к. обычно известны все факторы, оказывающие влияние на результативный признак. При функциональных связях величина результативного признака полностью показывается факторными признаками. Однако, в массовых явлениях общественной жизни в виду крайнего разнообразия факторов и их взаимосвязи и противоречивого действия этих факторов, не поддающихся строгому учету и контролю, возникает широкое варьирование результативного признака. Это свидетельствует о том, что связь между признаками неполная, а проявляется лишь в общем и среднем. Такие связи называются корреляционными. При корреляционной связи под влиянием изменения многих факторных признаков (ряд из которых может быть неизвестен), меняется средняя величина результативного признака. Пример, корреляционная связь между влиянием удобрения и урожайностью культур, между производительностью и энергооснощенностью предприятия. Важная особенность корреляционных связей состоит в том, что они обнаруживаются не в отдельных случаях, а в массовых общественных явлениях. Проявление корреляционных зависимостей подвержено действию закона больших чисел: лишь в достаточно большом числе фактов индивидуальные особенности и второстепенные факты сгладятся и зависимость проявится достаточно отчетливо. Вторая важная особенность корреляционных связей состоит в том, что эти связи неполные. Даже на массовых данных обнаруженные зависимости не будут носить полного, т.е. функционального характера. В зависимости от действия функциональных и корреляционных связей их делят на: прямые обратные Прямая связь – направление изменения результативного признака совпадает с направлением изменения признака фактора, т.е. с увеличением факторного признака увеличивается и результативный и наоборот. Обратная связь – направление изменения результативного признака не совпадает с изменением факторного признака, т.е. при увеличении факторного признака результативный уменьшается и наоборот. По форме связи бывают: 1. Прямолинейные – с возрастанием величины факторного признака происходит непрерывное возрастание результативного признака и наоборот. Математически такая зависимость представляется уравнением прямой: График представлен в виде прямой. Эту зависимость называют линейной. 2. Криволинейные – с возрастанием величины факторного признака изменение результативного признака происходит неравномерно, направление его может даже меняться. Графически этот процесс представлен гиперболой, параболой и ломаной. Для корреляционных связей есть различия в том случае, если: исследуется связь между одним признаком – фактором и результативным признаком; исследуется связь между несколькими признаками – факторами и результативным признаком. В первом случае имеет место парная связь и парная корреляция, во втором случае многофакторная связь и множественная корреляция. Для исследования функциональных связей применяется индексный и балансовый метод. 3. Балансовый метод изучения взаимосвязи. Статистический баланс представляет собой систему показателей, которая состоит их 2-х сумм абсолютных величин, связанных между собой законом равенства: Эту сумму можно представить следующим равенством: остаток на начало + приход = расход + остаток на конец.
Балансовый метод дает возможность не только анализировать показатели во взаимосвязи, но и осуществлять взаимный контроль данных и рассчитывать недостающие показатели. Пример, продано в розницу = остаток на начало + приход – продано оптом – остаток на конец. 4. Измерение тесноты связи между атрибутивными признаками. Коэффициент взаимной сопряженности Чупрова. Для измерения тесноты связи согласованного варьирования атрибутивных варьирующих признаков применяются различные показатели, наиболее общим из них является коэффициент взаимной сопряженности Чупрова. Он применяется для сопряжения связи двух атрибутивных признаков, когда это варьирование образует 3 и более группы. Пример, распределение 500 студентов заочников по оценкам на экзамене и характеру работы.
1,0436 – эта сумма за вычетом единицы называется показателем взаимной сопряженности и обозначается 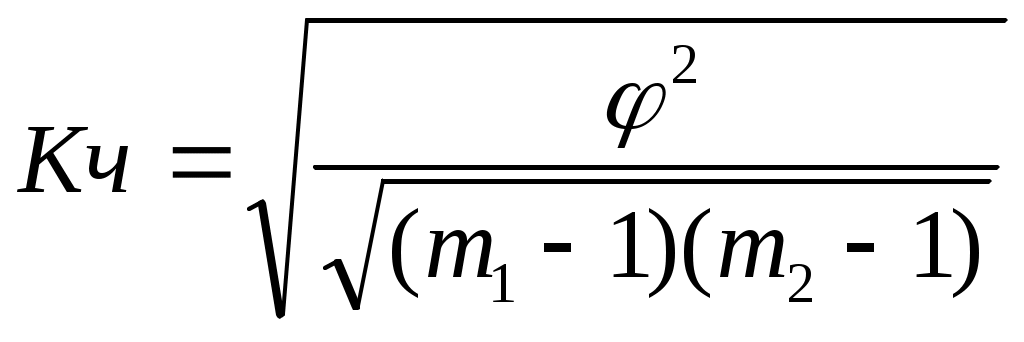 , ,где m – число групп по каждому признаку. Кч изменяется от 1 до 0, но уже при значении 0,3 можно судить о тесной связи между вариацией изучаемых признаков. Коэффициент ассоциации. Если вариация обоих атрибутивных признаков ограничена двумя группами, то коэффициент Чупрова может быть определен проще, в виде коэффициента ассоциации. Для этого исходные данные сводятся в комбинированную четырех клеточную таблицу.
Ка рассчитывается по формуле: Пример, распределение населения на городское и сельское по переписям.
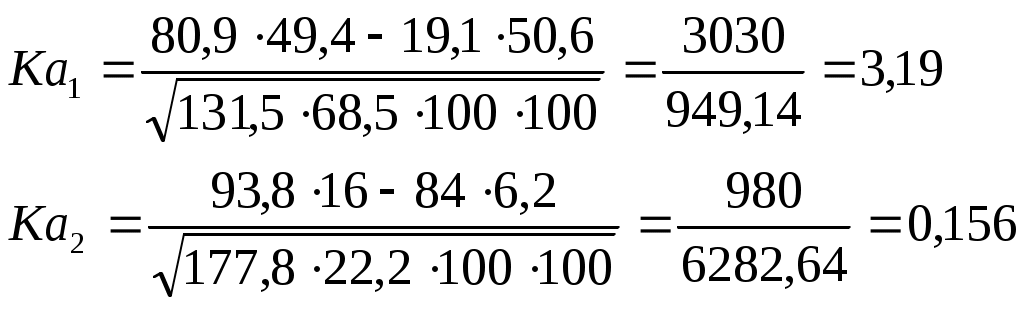 Ка изменяется от –1 до +1. Чем ближе он к крайним значениям, тем сильнее связаны между собой изучаемые признаки. 5. Метод сравнения параллельных рядов. После того, как на основании теоретического анализа будет выявлено, что между изучаемыми явлениями существует взаимосвязь, необходимо выявить тесноту этой связи. Это можно сделать с помощью параллельных рядов, для этого факторы, характеризующие результативный признак располагаются в возрастающем порядке, т.е. составляется ранжированный ряд, параллельно записываются признаки фактора. Путем составления, расположенных таким образом рядов, определяются существенные связи и их направления. Пример, уровни энерговооруженности (х) и производительности труда (у) по 15 заводам.
Рассматривая данные таблицы можно заметить, что с возрастанием признака х возрастает и признак у. Для сравнительного анализа параллельных рядов могут применяться элементарные показатели к которым можно отнести: коэффициент Фехнера (Кф), который оценивает связь на основе сравнения признаков с их средней арифметической. 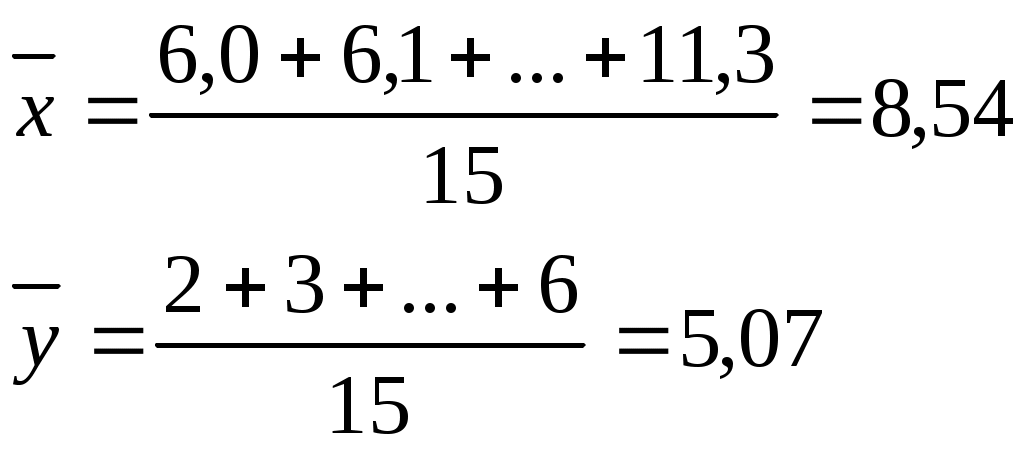
где С – число совпадений знаков х и у; Н – число несовпадений знаков х и у Кф изменяются от +1 до –1. Если Кф равен +1, то имеет место полностью согласованная прямая изменчивость. Если коэффициент равен 0 – изменчивость не согласуется. Если коэффициент равен –1, то полная обратная согласованная изменчивость. - коэффициент корреляции рангов . он учитывает согласованность рангов, которые представлены в виде номеров, присвоенных единицам совокупности по каждому из признаков: n – число единиц в совокупности; d – разность рангов. 6. Метод аналитических группировок. Значительно более сильно будет выделяться корреляционная зависимость, если применять метод группировки и сравнивать не индивидуальные значения, а групповые средние. Такой прием единственно возможный, если нужно выявить зависимость на примере 100, 1000 единиц. При этом необходимо образовать такое количество групп, при котором в вариации групповых средних в максимальной степени будет проявляться влияние группировочного признака. Чем больше групп образуется, тем больше увеличивается межгрупповая вариация, но при этом нельзя растягивать группировку, особенно при небольшом числе наблюдений. В этом случае группы получаются малочисленные и средние из них будут носить случайный характер, а межгрупповая вариация будет отражать не только влияние фактора признака, но и других факторов. Следовательно, нужно выбрать оптимальное число групп для конкретного случая, чтобы групповые средние перестали носить случайный характер и с каждой новой группой имели тенденцию к росту или снижению. Составим группировку, состоящую из 4 групп: по энерговооруженности
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||