Лекции по статистике [Фляжникова]. Конспект лекций Дисциплина Статистика
 Скачать 1.67 Mb.
|
|
Тема 9. Ряды динамики 1. Понятие и виды рядов динамики. Статистика рассматривает общественные явления в непрерывном развитии. Ряд динамики – последовательно расположенные в хронологическом порядке показатели, характеризующие общественные явления и процессы в развитии. В ряду динамики для каждого отрезка времени приводится два показателя: показатель времени показатель уровня ряда (у). Кроме них могут также показываться производные. Исследование рядов динамики дает возможность показать развитие явления во времени, тенденции развития, темпы роста, основные пути развития. Ряды динамики могут состоять из - абсолютных; - относительных; - средних величин. Примером ряда динамики средних величин является урожайность культур по хозяйствам области; ср. производительности. Примером ряда динамики относительных величин может быть ряд, характеризующий темпы роста производства продукции. Ряд динамики абсолютных величин характеризует уровни развития общественных явлений, либо на определенные моменты времени, либо за определенные промежутки времени. В зависимости от этого ряды динамики делят на: интервальные; моментные. Разница между ними заключается в том, что в моментном ряду интервал – это промежуток времени между датами, а в интервальном – это промежуток времени, за который обобщены приводимые сведения. На основе ряда динамики абсолютных величин могут быть получены ряды динамики относительных и средних величин. 2. Сопоставимость уровней ряда динамики. Анализировать ряды динамики нельзя, если приводятся несопоставимые данные. Несопоставимость статистических данных во времени может быть вызвана следующими причинами: инфляционным процессом; территориальные изменения; изменения единиц счета; изменения курса валют; изменения степени охвата статистического наблюдения; несовершенство методологии статистического наблюдения. Для того, чтобы привести уровни ряда в ряду динамики к сопоставимым уровням ряда необходимо провести смыкание рядов динамики. Это можно сделать лишь в том случае, если один из уровней ряда имеется в старом и новом исчислении.
1).  - коэффициент переоценки2).  - уровень стоимости О.Ф. для 1995г.3. Статистические показатели динамики социально-экономических явлений. Для количественной оценки динамики проводят расчет таких показателей, как абсолютный прирост, темп роста, темп прироста, темп наращивания, средний абсолютный прирост, средний темп роста. В основе расчета показателей ряда динамики лежит сравнительный анализ уровней ряда либо с постоянной, либо с переменной базой сравнения. При постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же показателем (уровнем), принятым за базу (у0). При переменной базе сравнения каждый уровень ряда сравнивают с предыдущим (  ).1. Абсолютный прирост – это разность 2 уровней ряда в исходных единицах измерения: - базисный  - цепной абсолютный  Абсолютный прирост может иметь отрицательное значение, если уровень изучаемого периода ниже уровня базисного периода или предшествующего. Между цепным и базисным абсолютным приростом существует взаимосвязь: сумма цепных абсолютных приростов равна абсолютному приросту последнего уровня ряда динамики:  2. Темпы роста – это отношение 2 уровней ряда, может выражаться в виде коэффициента, но чаще в %. Цепные  Базисные  Если темп роста > 100%, то идет увеличение изучаемого уровня по сравнению с базисным или предыдущим и наоборот. Между базисным и цепными темпами роста существует взаимосвязь – произведение последовательных цепных темпов роста равно базисному темпу роста последнего уровня ряда динамики. 3. Темпы прироста – характеризуют абсолютный прирост в относительных величинах. Определяется двумя способами: 1-й способ – путем вычитания из темпа роста 100%:  2-й способ – путем деления абсолютного прироста на уровень принятый за базу или предыдущий уровень ряда динамики:  - базисные   Если уровни ряда динамики сокращаются, то соответствующие показатели темпов прироста будут с минусом, т.к. они характеризуют уменьшение ряда динамики в %. 4. Темп наращивания – показывает в экономике наращивание во времени экономического потенциала. Вычисляется деление цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения:  Пример. Производственная мощность на предприятии характеризуется следующими данными: I. Интервальный ряд динамики «А»
Определить: 1. Все аналитические показатели ряда динамики «А». 2. Взаимосвязь цепных и базисных темпов роста. 3. Привести графическое изображение динамики производственной мощности. II. Моментный ряд динамики «В»
Привести расчет среднемесячного уровня остатков сырья на складе по данным моментного ряда динамики «В» по формуле средней хронологической для моментного ряда. I. 1). Абсолютный прирост Цепные: 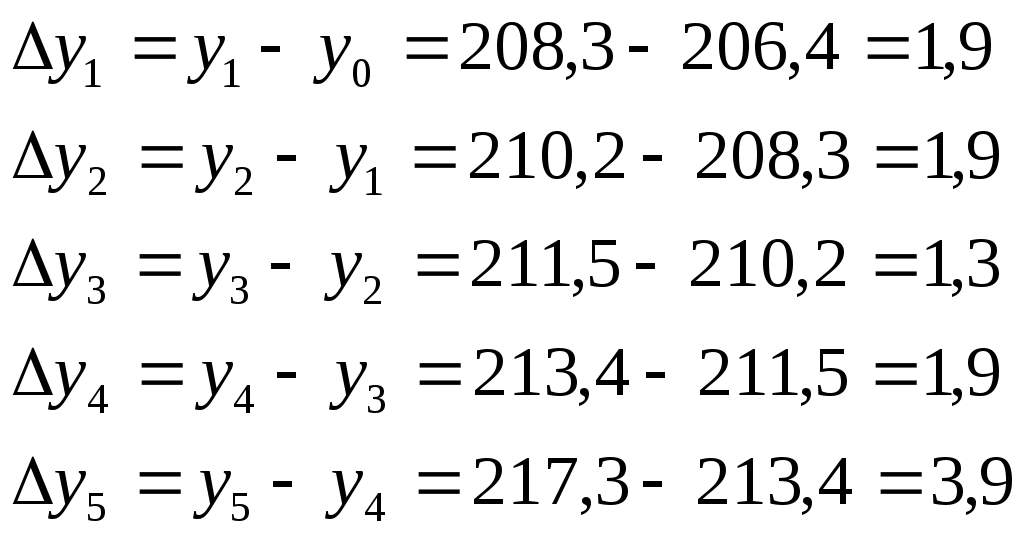 Базисные: 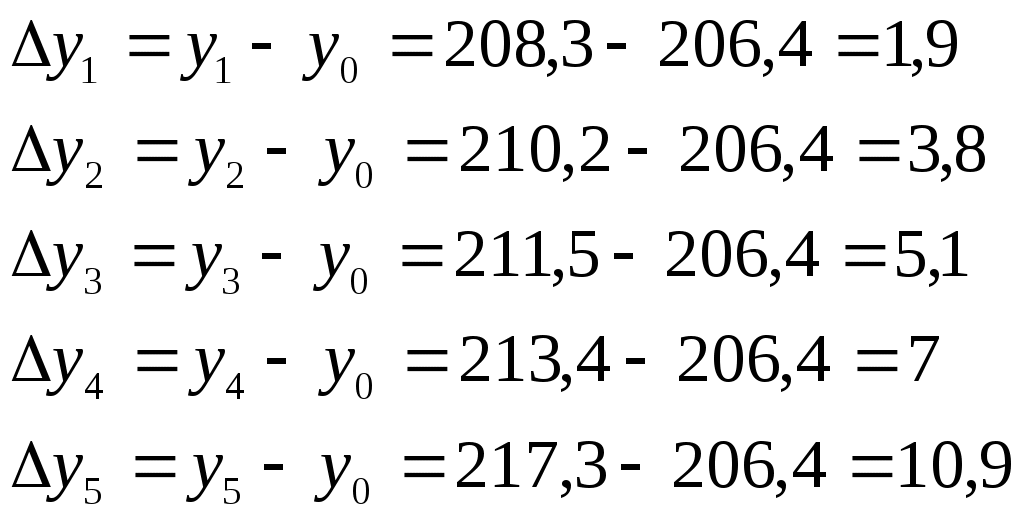 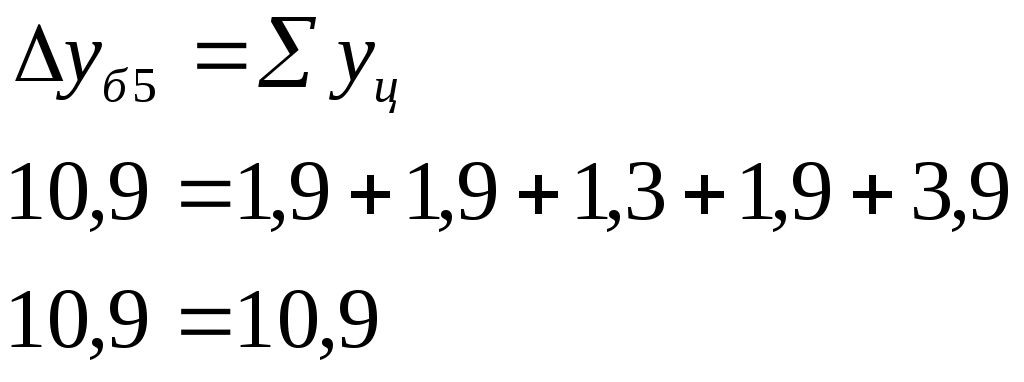 2). Темп роста Базисные: 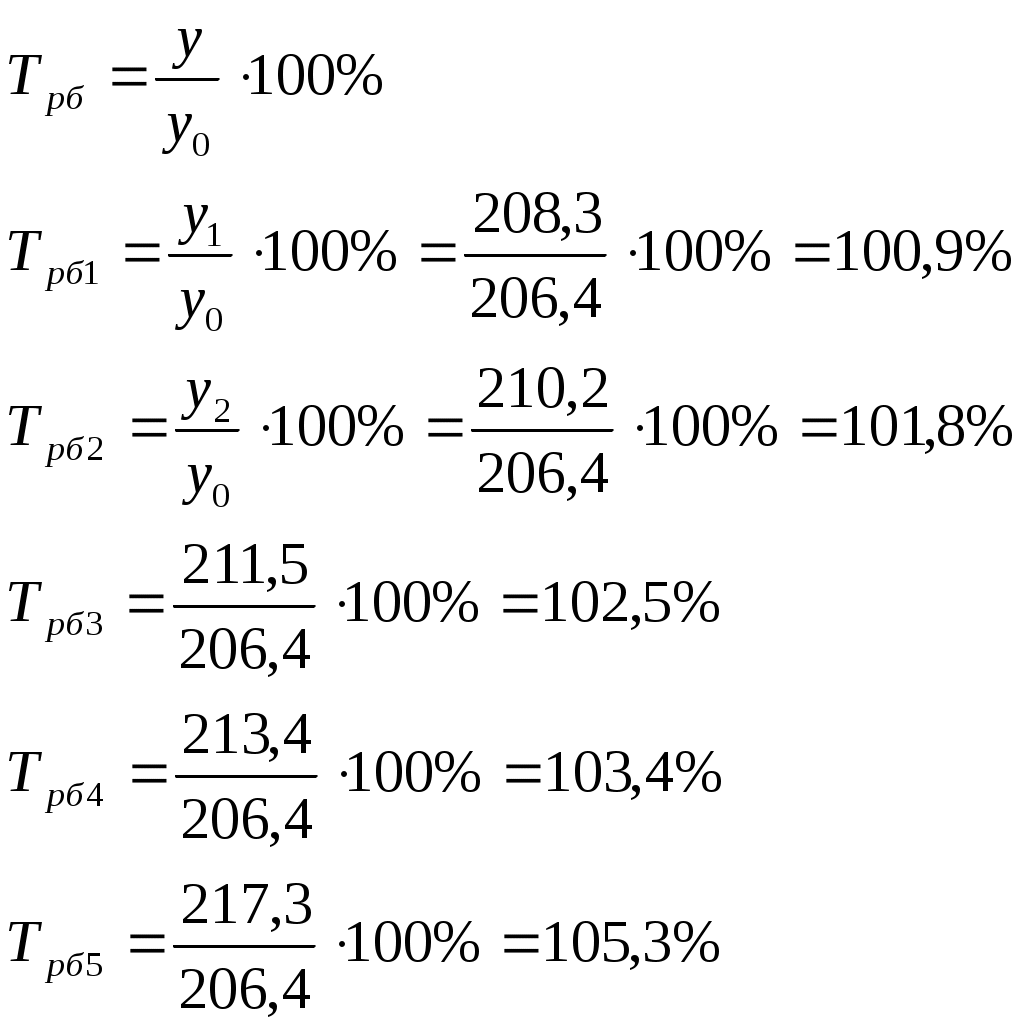 Цепные: 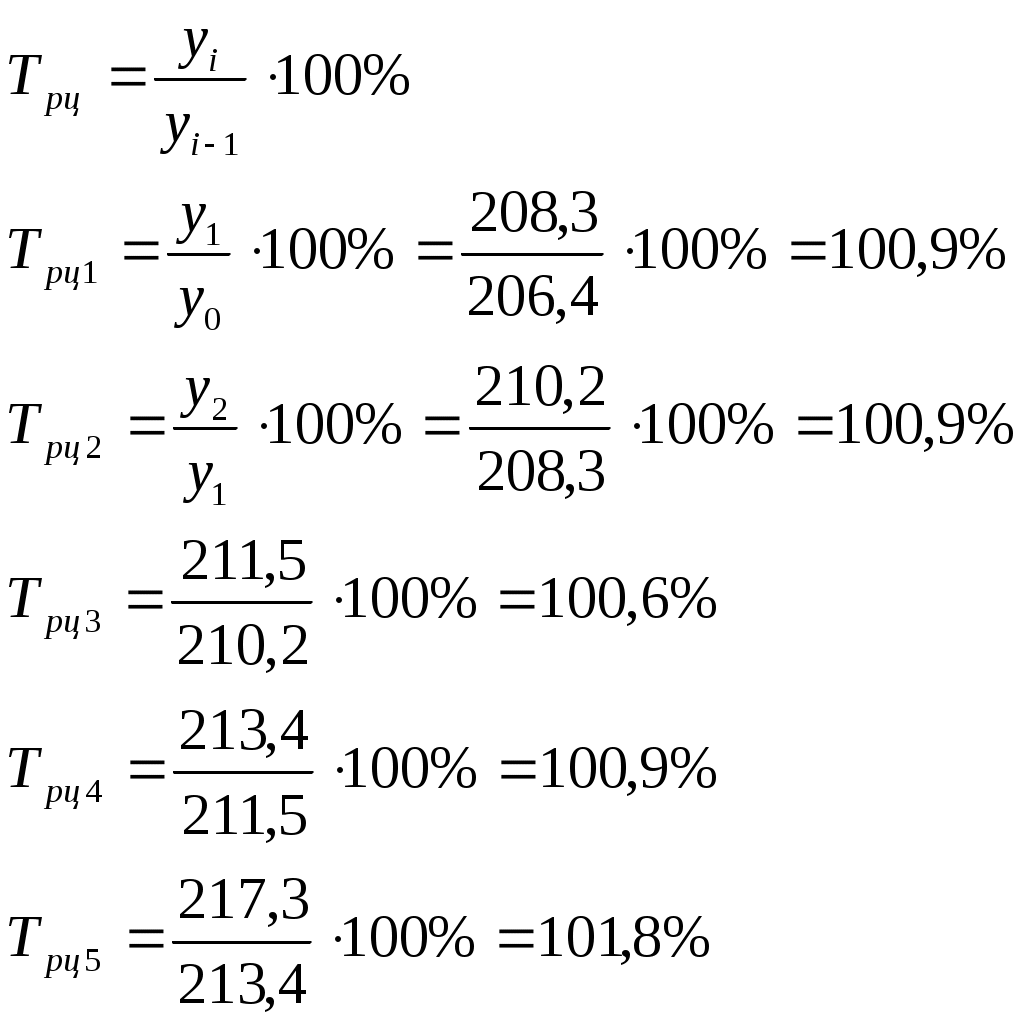 3). Темп прироста Базисные: 1-й способ: 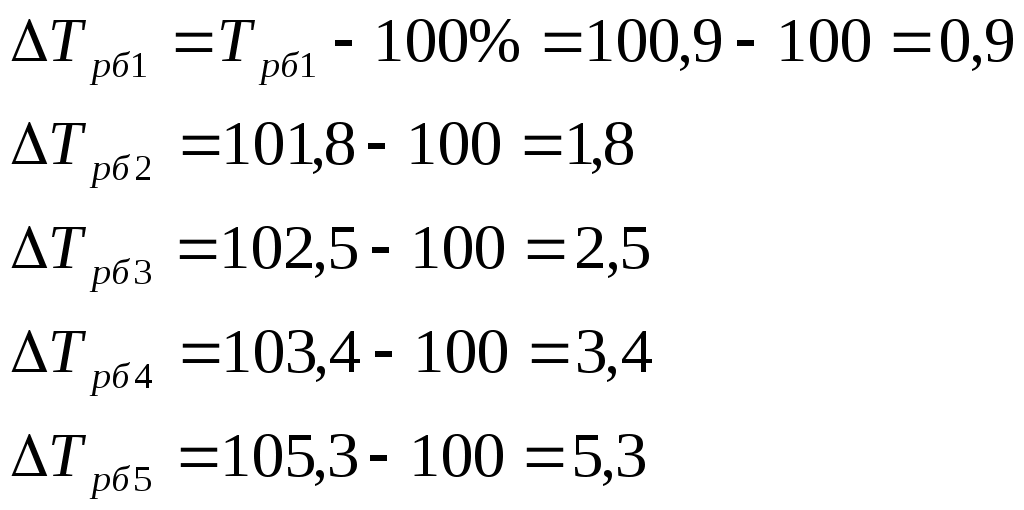  2-й способ:   и т.д.Цепные: 1-й способ:   2-й способ:   4). Темп наращивания: 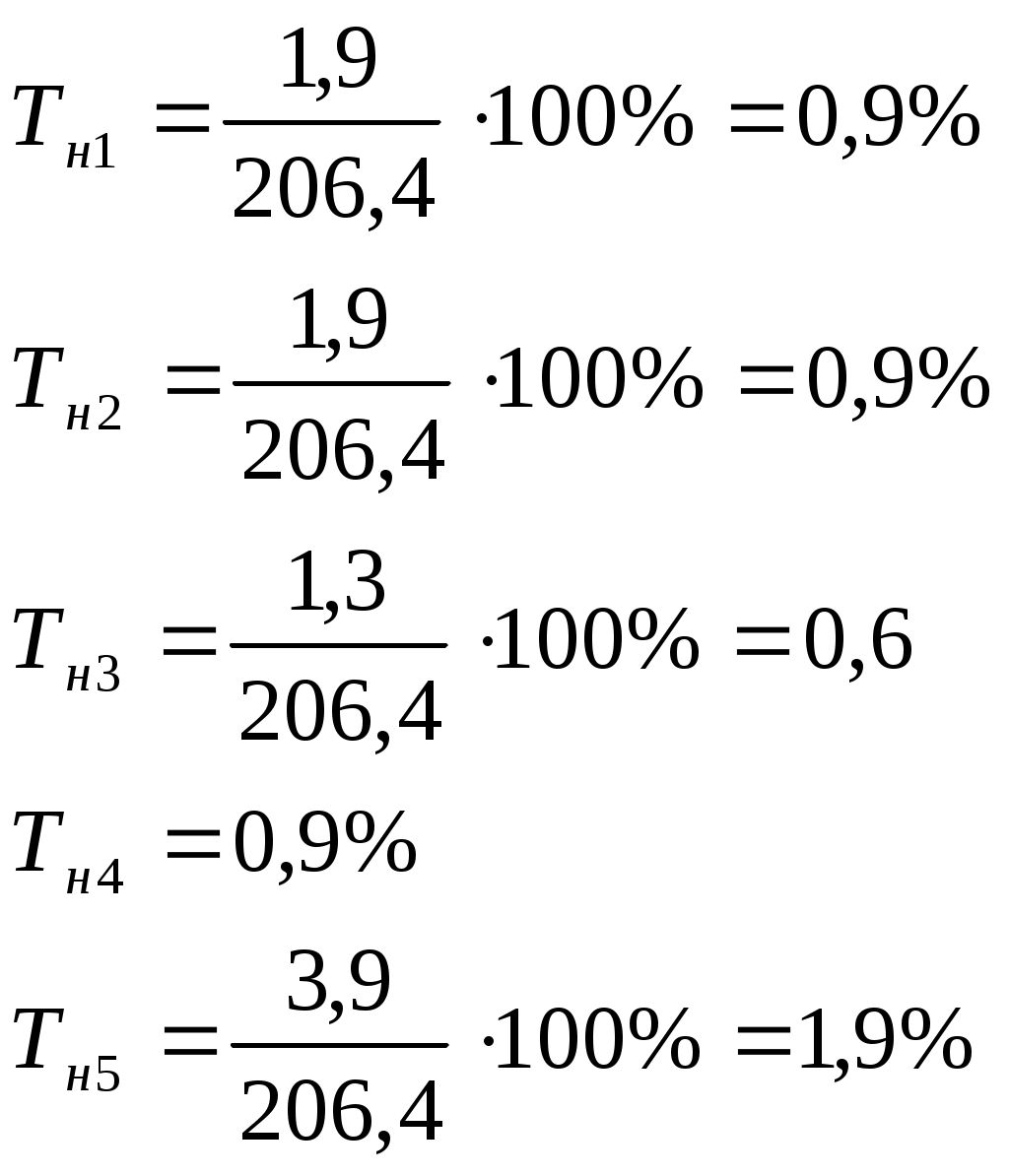  5). Средний абсолютный прирост: 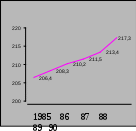   Рис. 7. Динамика производственной мощности 4. Анализ рядов динамики. Для анализа рядов динамики применяется сравнительный анализ, для того, чтобы выяснить какое явление развивается быстрее. Если сравниваются одноименные величины, то можно сопоставлять как абсолютные значения, так и относительные. Сравнительный анализ производства хлеба за сентябрь 1997г.
Если производится сравнительный анализ разноименных явлений, то сравнивать можно только относительные величины. Для этого определяют базисные темпы роста к какой-либо единой базе сравнения. Такой прием называется приведение рядов динамики к общему основанию. 5. Выявление основной тенденции динамики. При изучении динамики любого из явлений, главной задачей анализа ставится выявление основной тенденции в развитии. Количественная характеристика явления в динамике многих факторов и их развитии зависит от этих факторов. Пример, сезонные колебания. Для этого используют сглаживание рядов динамики по методу скользящей средней или по методу аналитического выравнивания уровней ряда динамики. Метод скользящей средней
1).  2). 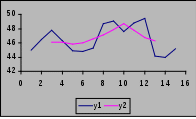 , и т.д. у1 – фактическая кривая у2 – сглаженная Рис. 8. Динамика выпуска продукции Для того, чтобы сгладить ряд по 5 дням необходимо по каждым последующим 5 дням рассчитать среднюю арифметическую простую, при этом среднее число за первых 5 дней поставить на 3-ю дату, а следующие 5 дней начинать рассчитывать со 2-го числа, а результат ставить на 4-ю дату. Чем больше интервал, за который исчисляется средняя, тем больше сглаженный ряд усредняет фактический ряд, при этом теряется много информации. Чем меньше интервал, тем больше сглаженный ряд приближается к конкретному ряду. По сглаженному ряду, показанному на графике можно выявить тенденцию в развитии. Метод аналитического выравнивания ряда динамики по прямой Если фактические уровни ряда динамики нанести на график, то получим ломаную линию, которая будет отражать как основные тенденции в развитии, так и отклонения от них, вызванные сезонными колебаниями или другими факторами. Чтобы выявить тенденцию необходимо выровнять ломаную линию, в основе выравнивания лежит теоретический анализ сущности данного явления и законы его развития. Как известно, уравнение прямой выражается следующей формулой:  , где  - значение уровней выровненного ряда динамики; - параметры прямой;t – показатель времени. Следовательно, задача сводится к тому, чтобы фактические уровни ряда динамики (у) заменить теоретическими уровнями ряда ( ). Прямая, выравнивающая ряд должна проходить в максимальной близости от фактических уровней ряда, т.е. сумма квадратов отклонений должна быть наименьшей. Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров  : 1.  2.  где, у – фактические уровни ряда, n – число уровней ряда. Для решения этого уравнения необходимо, чтобы сумма t была равна 0, для этого даты необходимо расположить так: –7-6-5-4-3-2-1 0 +1+2+3+4+5+6+7;  ,тогда уравнение принимает вид:  1.  
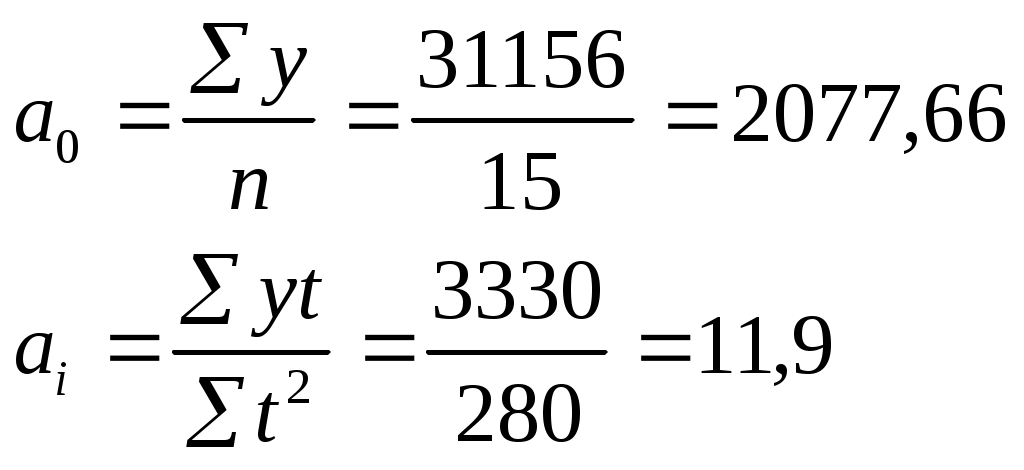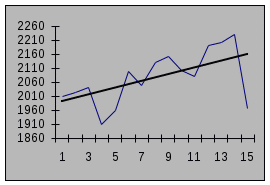    Рис. 9. Аналитическое выравнивание ряда динамики по прямой 6. Интерполяция и экстраполяция рядов динамики. Выравниванием рядов динамики пользуются для того, чтобы найти значение недостающего члена ряда. Такой способ называется интерполяцией. Экстраполяцией рядов динамики называют прием, который заключается в том, что, продолжая найденные математические кривые можно предсказать дальнейшее развитие событий. Прогнозирование базируется на знании развития прогнозируемого явления, а также факторов, влияющих на это явление и того, каким образом эти факторы могут изменить развитие явления. 7. Приемы изучения сезонных колебаний. Сезонное колебание – это более или менее устойчивые внутригодовые колебания в ряду динамики, обусловленные специфическими условиями производства или потребления данного товара. Сезонные колебания характеризуются индексами сезонности (JS) совокупность которых образует сезонную волну. Индекс сезонности - средняя величина, определенная из % отношений по одноименным месяцам фактических уровней ряда динамики к выровненным уровням. Для выявления сезонных колебаний берут данные за несколько лет с распр6еделением по месяцам, это делается для того, чтобы выявить устойчивую сезонную волну, на которой бы не отражались индивидуальные факторы одного года. Определяя индексы сезонности, пользуются несколькими методами, выбор которых зависит от вида ряда: 1). Если ряд содержит определенную тенденцию в развитии, то прежде чем определить сезонную волну, определяют общую тенденцию, при этом рассчитывают % фактических данных к выровненным, а индекс сезонности по формуле:  2). Если же ряд не содержит ярко выраженную тенденцию, то такой ряд называют стабильным, а индекс сезонности рассчитывают по формуле:  Пример, вычисление индексов сезонности в стабильном ряду динамики.
Р 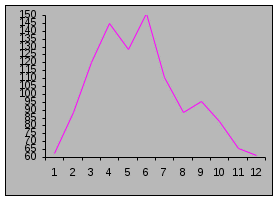 ис. 10. Индекс сезонности Пример, определить индекс сезонности реализации свежих фруктов в магазинах города (тонн).
Для упрощения расчетов обозначим t, таким образом, чтобы сумма tбыла равна 0 и: 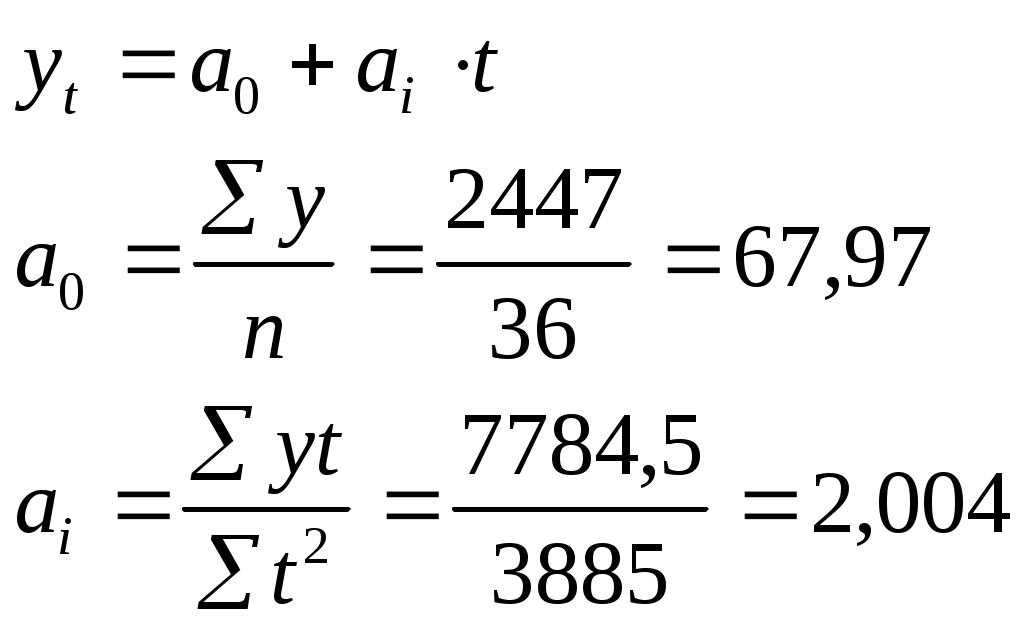 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
100
