Лекции по статистике [Фляжникова]. Конспект лекций Дисциплина Статистика
 Скачать 1.67 Mb.
|
|
Тема 7. Выборочное наблюдение 1. Понятие выборочного наблюдения. Выборочным называется такое наблюдение, при котором характеристика всей совокупности единиц дается по некоторой их части, отобранной в случайном порядке. Выборочное наблюдение относится к несплошному наблюдению. В практике выборочное наблюдение используется для контроля качества продукции, контроля за использованием рабочего времени, контроля за выполнением норм выработки и т.д. Широкое распространение выборочное наблюдение получило в связи с тем, что затраты не его проведение достаточно меньшие, чем на проведение сплошного наблюдения, и нередко выборочное наблюдение является единственно возможным. Например, проверка качества. Выборочное наблюдение дает возможность получить обобщающие показатели, правильно характеризующие всю совокупность, не исследуя совокупность в целом. Подлежащая изучению совокупность называется генеральной, а отобранная для наблюдения ее часть – выборочной (выборкой). Значение выборочного наблюдения в том, что данный метод повышает оперативность и уменьшает ошибки. Поскольку данная совокупность состоит из единиц с изменяющимися признаками. То состав выборки может отличаться от генеральной совокупности. В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей и обозначается Р, а средняя генеральная средней -  .В выборке доля изучаемого признака называется выборочной долей и обозначается W. А средняя выборочная средней -  .Частость определяется как отношение единиц, обладающих изучаемым признаком (  ), к общей численности единиц выборочной совокупности (п). 2. Понятие и расчет ошибки выборки. Задачей выборочного наблюдения является дача верных представлений о сводных показателях всей совокупности на основе некоторой их части, подвергнутой наблюдению. Возможное отклонение выборочной доли и выборочной средней от доли и средней в генеральной совокупности называется ошибкой выборки или ошибкой репрезентативности. Чем больше величина этой ошибки, тем больше показатели выборочного наблюдения отличаются от показателей генеральной совокупности. Различаются: ошибки выборки; ошибки регистрации. Ошибки регистрации возникают при неправильном установлении факта в процессе наблюдения. Они свойственны как сплошному наблюдению, так и выборочному, но в выборочном их меньше. По природе ошибки бывают: тенденциозные – преднамеренные, т.е. были отобраны либо лучшие, либо худшие единицы совокупности. При этом наблюдения теряют смысл; случайные – основной организационный принцип выборочного наблюдения состоит в том, чтобы не допустить преднамеренного отбора, т.е. обеспечить строгое соблюдение принципа случайного отбора. Общим правилом случайного отбора является: у отдельных единиц генеральной совокупности должны быть совершенно одинаковые условия и возможности упасть в число единиц, входящих в выборку. Это характеризует независимость результата выборки от воли наблюдателя. Воля же наблюдателя порождает тенденциозные ошибки. Ошибка выборки при случайном отборе носит случайный характер. Она характеризует размеры отклонений генеральных характеристик от выборочных. Формулы средней ошибки выборки. В связи с тем, что признаки в изучаемой совокупности варьируют, то состав единиц, попавших в выборку, может не совпадать с составом единиц всей совокупности. Это означает, что Р и не совпадают с W и . Возможное расхождение между этими характеристиками определяется ошибкой выборки, которая определяется по формуле: где  - генеральная дисперсия. где  - выборочная дисперсия.Отсюда видно, где генеральная дисперсия отличается от выборочной дисперсии в  раз. Существует повторный и бесповторный отбор. Сущность повторного отбора состоит в том, что каждая, попавшая в выборку единица, после наблюдения возвращается в генеральную совокупность и может быть исследована повторно. При повторном отборе средняя ошибка выборки рассчитывается:  Для показателя доли альтернативного признака дисперсия выборки определяется по формуле:  На практике повторный отбор применяется редко. При бесповторном отборе, численность генеральной совокупности N в ходе выборки сокращается, формула средней ошибки выборки для количественного признака имеет вид:  , тогда  Одно из возможных значений, в которых может находиться доля изучаемого признака равно: 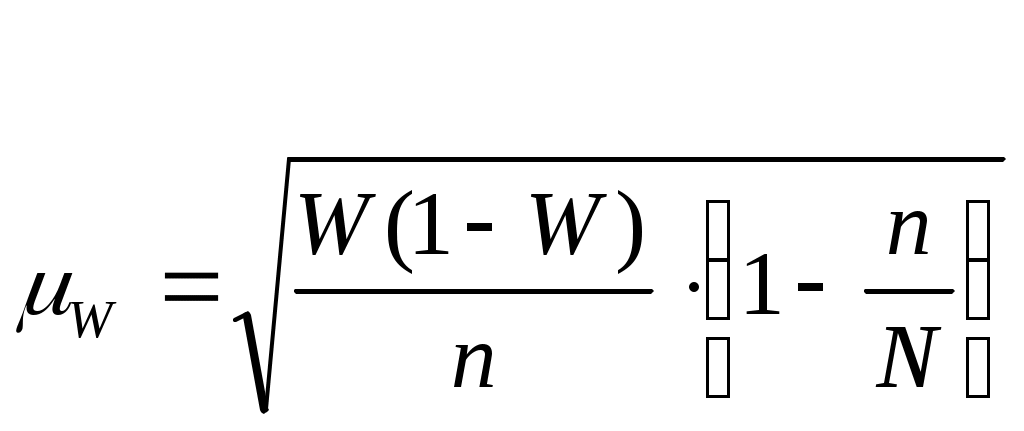  где  - ошибка выборки альтернативного признака.Пример. При выборочном обследовании 10 % изделий партии готовой продукции по методу без повторного отбора получены следующие данные о содержании влаг в образцах.
Определить средний % влажности, дисперсию, среднее квадратическое отклонение, с вероятностью 0,954 возможные пределы, в которых ожидается ср. % влажности всей готовой продукции, с вероятность 0,987 возможные пределы удельного веса стандартной продукции при условии, что к нестандартной партии относятся изделия с влажностью до 13 и выше 19 %. 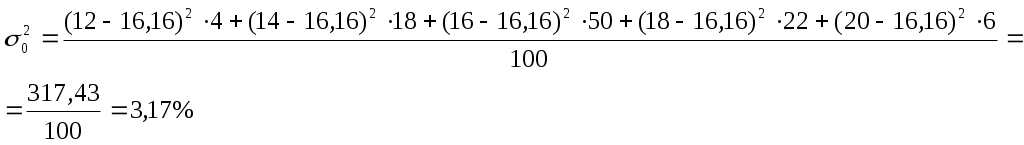    Лишь с определенной вероятностью можно утверждать, что генеральная доля от выборочной доли и генеральная средняя от выборочной средней, отклоняются в tраз. В статистике эти отклонения называются предельными ошибками выборки и обозначаются  . Вероятность суждений можно повысить или понизить в t раз. При вероятности 0,683 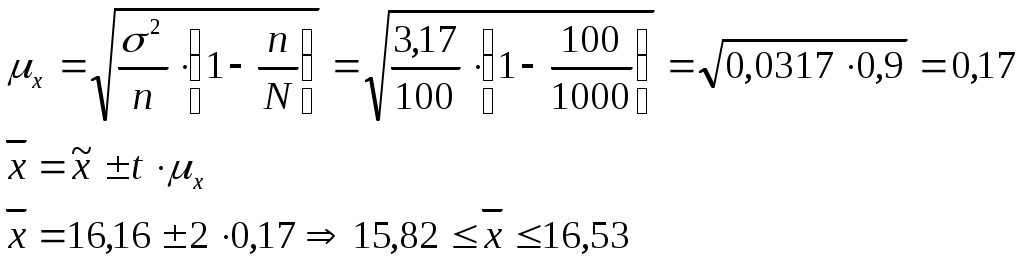 , при 0,954 , при 0,987 , тогда показатели генеральной совокупности по показателям выборки определяются:     Средний процент влажности генеральной совокупности может быть любым значением, находящемся в пределах от 15,82 до 16,33. 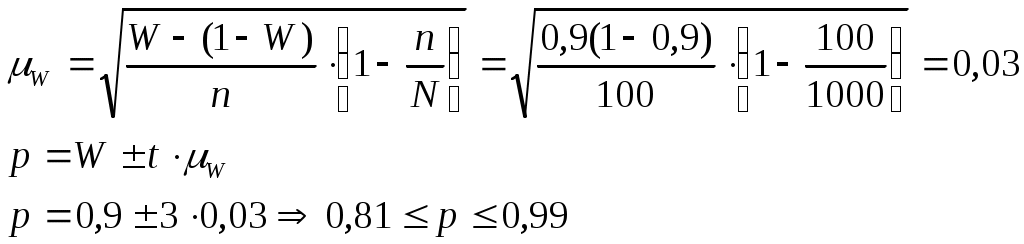;    Таким образом, удельный вес стандартных изделий в генеральной совокупности находится в пределах 81 % – 99 %. Из расчета задачи видно, что возможные пределы удельного веса единиц генеральной совокупности будут находиться:  А среднее значение генеральной совокупности находится в пределах :  Тема 8. Способы формирования выборочных с совокупностей 1. Районированный и нерайонированный отбор. Формирование выборочной совокупности происходит из единиц генеральной совокупности, причем, отбор может быть нескольких видов: нерайонированный отбор – отбор единиц в выборочную совокупность из генеральной совокупности не разбитой на группы по каким-либо признакам; районированный – генеральная совокупность делится на группы по признакам. Пример, отбор предприятий по отраслям. Разбивка генеральной совокупности на группы происходит по реально существующим признакам, в данном случае такой отбор называется типическим. Типический отбор облегчает формирование выборочных совокупностей и обеспечивает более равномерное распределение единиц в генеральной совокупности. При типическом отборе показатели выборочной характеристики, более точнее, чем при нерайонированном отборе. 2. Собственно-случайный отбор. Дает лотерея, жеребьевка или тираж, при этом обеспечивается абсолютно равная возможность попадания в выборку любой единицы. Пример, тираж «Русское лото» и попадание в выборку любого билета, при этом ошибка выборки определяется по формуле:  3. Механический отбор. Составляют список всех единиц совокупности и определяют интервал путем деления числа генеральной совокупности на число выборочной совокупности.  Поэтому в выборочную совокупность войдут единицы генеральной совокупности, расположенные в списке через данный интервал. Принцип случайного отбора в механической выборке обеспечивается тем, что единицы в генеральной совокупности располагаются в таком порядке, который не оказывает влияние на изучаемый признак или фактор. Механический отбор можно использовать и без применения списков, а брать единицы так, как они располагаются в генеральной совокупности. Пример, при 2 % отборе из 100 единиц в выборку попадает каждый 50-й. Ошибка выборки при механическом отборе, рассчитывается исходя их внутригрупповой дисперсии или средней из групповых дисперсий. Однако, если генеральная совокупность разбита на группы по строго нейтральному признаку, то ошибку выборки, исходя из внутригрупповой дисперсии, определить нельзя, т.к. внутригрупповая равна общей дисперсии. 4. Типический отбор. Данный отбор состоит из 2 этапов: определяют признак, по которому проводится районирование генеральной совокупности; в группах проводят механический отбор единиц выборочной совокупности. При этом ошибка выборки рассчитывается: 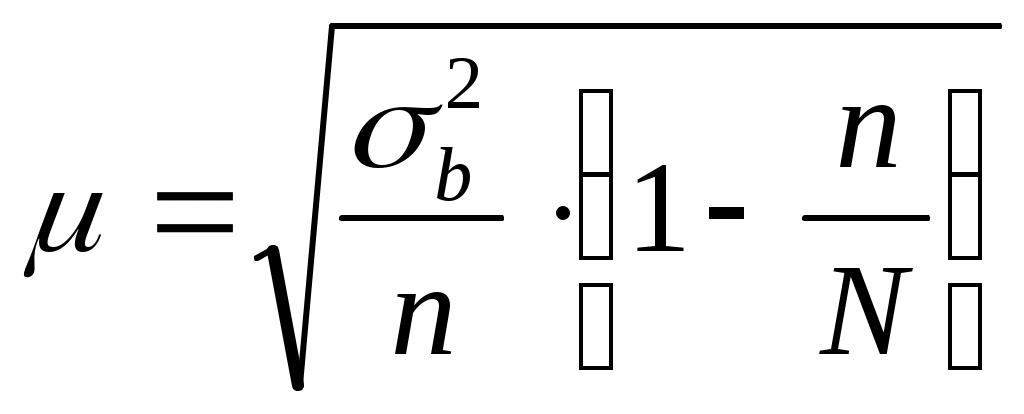 где  исходя из закона сложения дисперсии равна разности общей дисперсии и межгрупповой дисперсии, т.е. С помощью корреляционного отношения, которое определяется как корень квадратный из частного межгруппового и общей дисперсией: 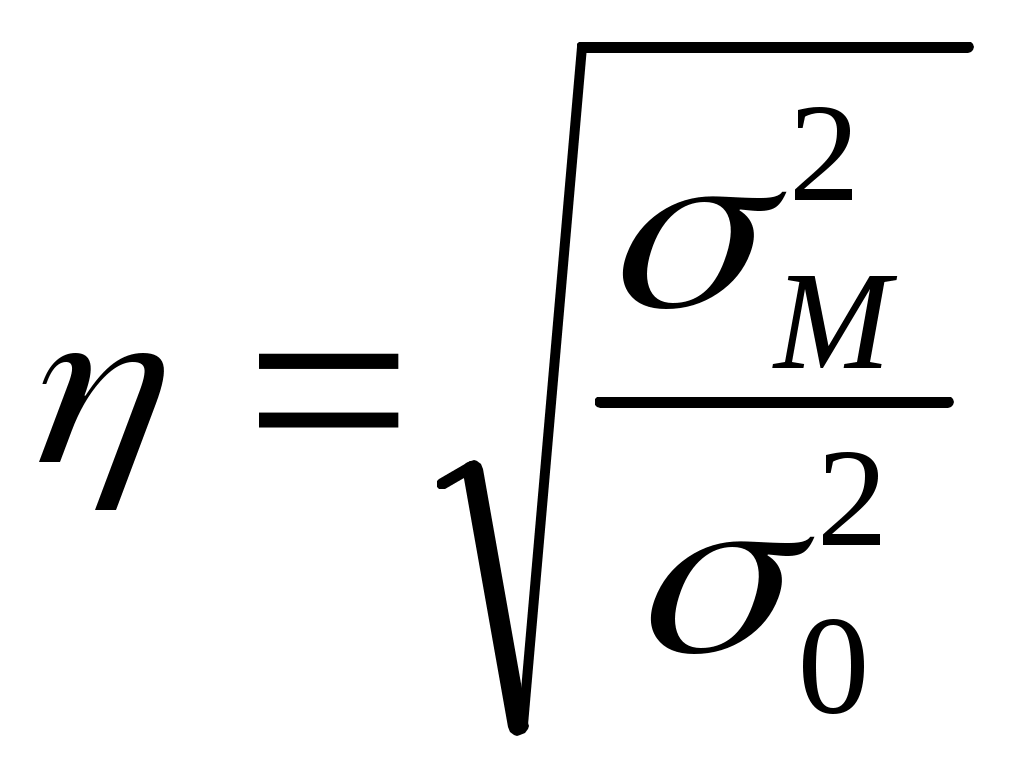 В связи с этим, дисперсия выборочной средней в типической выборке равна:  Следовательно, типизация уменьшает ошибку выборки на  Численность единиц выборочной совокупности между группами обычно распределяется пропорционально численности по группам единиц в генеральной совокупности в группах на соответствующие групповые средние квадратические отклонения. Разновидностью типической выборки является систематический отбор, т.е. механический отбор из совокупности ранжированной по какому-либо признаку, связанному с изучаемым признаком. Пример, отбор рабочих по семейному бюджету, связанному с их средней заработной платой. 5. Многоступенчатая выборка. Типичный отбор состоит в многоступенчатой выборке из сочетания нескольких стадий отбора, причем на каждой стадии имеется своя единица отбора (отрасль предприятия, численность и средняя заработная плата.). Пример, проведем многоступенчатую выборку. В области имеются 13 предприятий общей численностью 40 тыс. человек. Требуется 200 человек так, чтобы с каждого предприятия было 25 работников с различным уровнем заработной платы.
I ступень. Определим число предприятий, попадающих в выборку:  предприятий.Для того, чтобы приступить к отбору предприятий, определим величину интервала  Каждый 5000-ый работник попадает в выборку:
II ступень. Проверяем репрезитивность средней заработной платы. по всем предприятиям:  Выборочные данные репрезитивны, т.к. выборочная средняя ненамного отличается от общей средней. III ступень. Определим рабочих внутри предприятия. Рабочих делят на квалифицированных и неквалифицированных. Так по данным 1-го предприятия из 6800 человек 5440 являются квалифицированными, значит, 4/5 квалифицированные, а 1/5 – неквалифицированные, т.е. из 25 рабочих 20 войдут в первую группу, пять во вторую. Далее составляют 2 списка по квалификациям и определяют интервал внутри каждого списка:  Таким образом, 272-ой рабочий по списку войдет в выборку. Далее по другим предприятиям аналогично. Из этого видно, что предприятия в пределах отрасли отбирают механическим отбором с последующей проверкой репрезитивности по среднему уровню заработной платы. Рабочих же выбирают на основе пропорционально типическому отбору. Многоступенчатый отбор принимают при наличии нескольких типов единиц отбора, которые отличаются по своим масштабам, при этом необходимо так организовать выборочное исследование, чтобы оно равномерно распределялось между отдельными частями сложного явления. 6. Многофазная выборка. Отличается от многоступенчатой тем, что на всех ступенях обследуется одна и та же единица отбора (обследование крестьянских хозяйств, где более полно обследуется каждое 3-е, 9-е, 27-е и т.д. хозяйство, при этом ошибка выборки незначительна и выборочные показатели более точно характеризуют генеральную совокупность). 7. Комбинирование выборочного наблюдения со сплошным. Характерно для многофазной выборки. Оно позволяет проверить более точно типичность выборочных данных по отношению к генеральным характеристикам. Выборочные показатели сопоставляются с данными сплошного наблюдения. 8. Серийная выборка. Если в выборку попадают не отдельные единицы совокупности, а целые серии, такая выборка называется серийная. Пример, при 10 % обследовании качества продукции можно проверять каждую 10-ю единицу (механический отбор), при серийном – через 9 часов каждый 10-й час обследуется вся выпущенная продукция в течении целого часа. Серийный отбор применяется редко, т.к. дает высокую ошибку выборки. 9. Моментная выборка. На определенные моменты времени фиксируется наличие отдельных элементов изучаемого процесса. Пример, изучение использования работниками рабочего времени и времени работы оборудования. Моментное наблюдение охватывает все единицы совокупности, поэтому является сплошным. Цель – на основе выборочных характеристик дать репрезентативную оценку всей генеральной совокупности. Т.к. при моментном наблюдении обычно характеризуется альтернативный признак (работа или простой), то оценка репрезентативности проводится по формулам средней и предельной ошибки выборки. При этом, в качестве численности выборочной совокупности, принимается число записей моментного обследования. Пример, в цехе работает 20 станков. За 8-ми часовую смену каждые полчаса проводились моментные обследования. Определить в каких пределах будет находиться доля работающих станков за все время смены, если в 32 случаях замечен простой, вероятность 0,954. 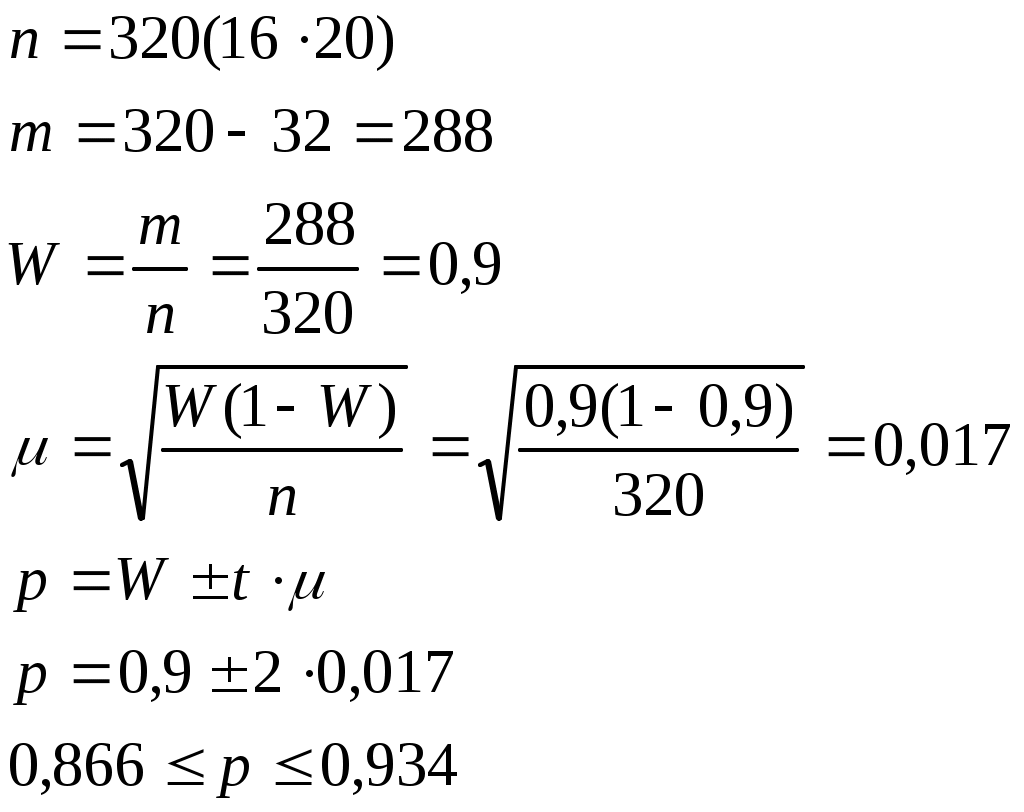 10. Малая выборка. Такое выборочное наблюдение, численность единиц которого не более 20. Хотя общий принцип выборочного наблюдения – чем больше выборочная совокупность, тем точнее показатели, иногда используют малую выборку. Малая выборка применяется при обследовании качества продукции с последующим уничтожением проверяемой единицы. Средняя ошибка малой выборки определяется по формуле:  Причем, малая выборочная дисперсия рассчитывается:  Следовательно, предельная ошибка выборки:  Но в данном случае коэффициент доверия – tотличен от применяемого t в других выборочных наблюдениях. Он зависит от n(числа выборки), при увеличении n распределение стремится к нормальному и при n = 20 мало чем отличается от нормального. Если n = 20; t = 1  вероятность = 0,683.t = 2 0,954t= 3 0,99711. Проверка типичности выборочных данных. Кроме вероятностной оценки репрезентативности выборочных данных путем расчета средней и предельной ошибки выборки по каждому показателю проверка типичности часто осуществляется путем сопоставления выборочных данных с данными сплошного отбора. Пример, обследование уровней заработной платы. Типичность отобранных предприятий проверяется путем сравнения средней заработной платы на отобранных предприятиях со средней заработной платой всех предприятий. Существует 2 способа распространения данных выборочного наблюдения: - способ прямого пересчета пример, надой с одной коровы за год составил 2500 л. Среднее поголовье коров в частном владении 10000 голов. Ошибка выборки составляет 20 л. Определить годовой надой со всего поголовья имеющихся у селян:  Способом прямого пересчета можно распространять данные выборочного наблюдения на основе соотношения численности выборочной и генеральной совокупности. Пример, при выборочном 3 % обследовании качества продукции в выборку попало 1000 единиц, из которых качество 20 не соответствует стандарту. Ошибка выборки =  2 единицы. Используя соотношение численности можно рассчитать, что число некачественных единиц из 20000 будет равно:  от 360 до 440 - способ коэффициентов, применяют при проведении выборочного наблюдения для проверки и уточнения данных сплошного обследования. Сопоставляя выборочные данные с данными сплошного наблюдения, определяют поправочный коэффициент, а с его помощью вносят поправки в данные выборочной совокупности. |
1,5737