ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"

• Название: Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
• Дата: 30.03.2022
• Размер: 1.06 Mb.
• Имя файла: ЛекцПРиА.docx
• Тип: Конспект; #429098
• страница: 12 из 14

2.11. МОДЕЛИРОВАНИЕ И МЕТОД
АНАЛИЗА РАЗМЕРНОСТЕЙ

Часто исследования с помощью теории подобия процессов и аппаратов проводят не на реальных объектах, а на установках значительно меньшего размера. Такой метод исследования называют моделированием. Для сложных процессов, например каталитических, подобное преобразование дифференциальных уравнений приводит к выводу зависимостей между большим числом критериев подобия. Надежное моделирование таких процессов на малой опытной установке с последующим распространением полученных данных на производственные условия, то есть применение изложенных выше принципов так называемого физического моделирования, практически невозможно. В связи с этим физическое моделирование процессов приходится проводить последовательно на ряде опытных установок, постепенно приближающихся по масштабу к промышленным установкам. Такое моделирование сопряжено с большими затратами времени и средств.

Значительно более эффективно аналоговое моделирование, когда модель по конструкции отличается от реального устройства и протекающий в ней процесс имеет физическую природу отличную от исследуемого процесса. В основе такого моделирования лежит свойство изоморфизма

(одинаковой формы) дифференциальных уравнений, описывающих различные по физической сущности процессы: электрические, гидродинамические, тепловые, массообменные и другие. Эти процессы описываются однотипными дифференциальными уравнениями, что является отражением единства законов природы:

перенос электричества (закон Ома)

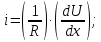(2.182)

перенос количества энергии (закон внутреннего трения Ньютона)

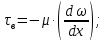(2.183)

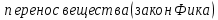
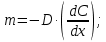(2.184)

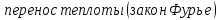
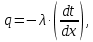(2.185)

где dU/dx, d 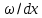, dC/dx, dt/dx – градиенты напряжения электрического поля, скорости, концентрации и температуры, соответственно;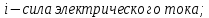

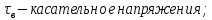
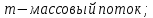
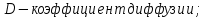
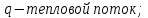
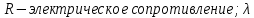– коэффициент теплопроводности.

Уравнения (2.180) – (2.183) являются частными случаями общего кинетического уравнения (1.8). Одинаковая форма этих уравнений позволяет, например, для изучения тепловых процессов использовать явления массопереноса или гидродинамические процессы моделировать тепловыми явлениями и так далее.

Самое большое практическое значение имеет применение электрических моделей. Их преимущества перед другими моделями состоят в самом высоком быстродействии, в изменении значений переменных в самом широком диапазоне, в наличии аналогии между электрическими явлениями и математическими действиями. Последнее преимущество электрических явлений позволяет осуществлять математическое моделирование, то есть изучать процессы с применением аналоговых и электронных вычислительных машин. Математическое моделирование особенно ценно, когда решения дифференциальных уравнений другими методами получить не удается. Таким образом, математическое моделирование является одной из разновидностей аналогового моделирования.

Еще одним методом теории подобия является метод анализа размерностей. Его применяют для исследования очень сложных процессов, для которых нельзя получить полного математического описания, а можно лишь в самом виде представить зависимость между различными переменными, влияющими на протекании процесса.

В основе метода анализа размерностей кроме теории подобия лежит еще 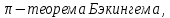согласно которой общую функциональную зависимость, связывающую между собой 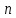переменных величин при 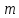основных единицах измерения, можно представить в виде зависимости между 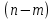безразмерными комплексами этих величин, а при наличии подобия – в виде связи между ( 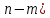критерими подобия.

Рассмотрим использование этой теоремы применительно к движению жидкости по трубопроводу, основной характеристикой которого является перепад давления 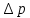между различными точками по длине трубопровода. На основании экспериментов известно, что 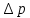зависит от диаметра 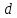и длины 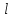трубопровода, плотности жидкости 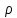, вязкости 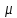и скорости течения жидкости 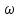. Функциональная зависимость в общем виде запишется так:

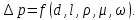(2.186)

Единицы измерения всех единиц должны быть выражены в одной системе.

В функциональную зависимость (2.186) входят шесть величин ( 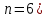, которые в системе СИ имеют следующие единицы измерения и размерности:

] = [ ] = [ ];

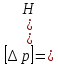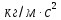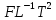[d]=[м]=[L]; [ 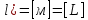; [ 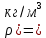] = [F ];

[ ] = [ ]; ].

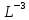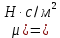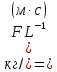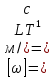При составлении этих размерностей использованы три основных единицы измерения ( 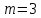) м, кг, с. Следовательно, функциональная зависимость (2.186) должна содержать 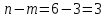критерия подобия.

Представим зависимость (2.186) в виде степенной функции

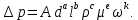(2.187)

Заменив величины формулами их размерностей

[ ]=

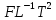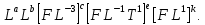(2.188)

Раскрывая скобки, получим

[ ] =

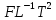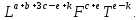(2.189)

Приравняем показатели степеней при одинаковых размерностях и получим систему из трех уравнений с пятью неизвестными

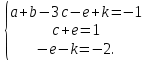(2.190)

Выразив 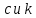из второго и третьего уравнений и подставим их в первое уравнение системы, получим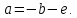

Полученные значения 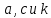подставим в исходное уравнение (2.187) и после группировки величин по показателям степеней получим критериальное уравнение в виде

.

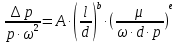(2.191)

Значения постоянных величин 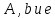находят опытным путем. Причем известно что, b=1, а значит величин 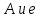зависят от режима движения жидкостей в трубопроводе.

Заключительными этапами в исследовании процессов и аппаратов являются масштабирование, то есть переход от модели к производственному аппарату, и оптимизация.