ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"

• Название: Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
• Дата: 30.03.2022
• Размер: 1.06 Mb.
• Имя файла: ЛекцПРиА.docx
• Тип: Конспект; #429098
• страница: 11 из 14

2.10. МЕТОДЫ ИССЛЕДОВАНИЯ ТИПОВЫХ ПРОЦЕССОВ
И АППАРАТОВ В БИОТЕХНОЛОГИЧЕСКОМ ПРОИЗВОДСТВЕ. ТЕОРИЯ ПОДОБИЯ

Основными методами исследования процессов и аппаратов в биотехнологическом производстве являются: теоретический метод, экспериментальный метод; методы теории подобия, которые включают методы моделирования и анализа размерностей.

Теоретический метод основан на составлении и решении дифференциальных уравнений, описывающих процесс. Эти уравнения вытекают из общих законов химии, физики, биохимии и биофизики. Они применимы к целому классу однородных явлений. Поэтому для конкретного процесса и аппарата они должны решаться с введение дополнительных ограничивающих условий (условий однозначности). Условия однозначности включают: форму и размеры системы, т. е. аппаратуры, в которой происходит процесс; существенные для данного процесса физические константы участвующих в нем веществ; начальные условия, к числу которых относятся: начальная концентрация, начальная скорость и т. п.; граничные условия, характеризующие состояния на границах системы (концентрацию, температуру, давление и т. д.), например, в гидродинамических процессах равенство нулю скорости движения жидкости у стенок.

Однако многие процессы характеризуются большим числом переменных и настолько сложны, что удается только дать математическую формулировку задачи и выявить условия однозначности. Полученные же дифференциальные уравнения не могут быть решены известными в математике методами. Таким образом, теоретический вывод расчетных зависимостей, необходимых для проектирования аппаратуры, часто оказывается невозможным.

В таких случаях для нахождения связи между величинами, характеризующими процесс, прибегают к экспериментальному методу, т. е. к проведению опытов. На основе опытных данных получают эмпирические уравнения, которые имеют известную ценность и используются в инженерной практике. Однако эти уравнения являются частными и не могут быть распространены на условия отличные от тех, для которых они получены. Гораздо более плодотворными являются методы исследования, позволяющие теоретически обобщать результаты опытов и распространять их на широкий круг явлений, подобных изученному процессу, но отличающихся численными значениями полученных параметров, например, размерами аппаратов, величинами основных функциональных свойств среды и т. д. Это достигается при использовании для обработки опытных данных методов теории подобия.

Теория подобия является учением о методах научного обобщения экспериментов. Она указывает, как нужно ставить опыты и как обрабатывать их результаты, чтобы при проведении небольшого числа экспериментов иметь возможность обобщать опытные данные, получая единые уравнения для всех подобных явлений. Теория подобия позволяет вместо дорогостоящих экспериментов на промышленной аппаратуре выполнять опыты на моделях. Опыты можно проводить не с рабочими (часто вредными и опасными веществами) и не в жестких (высокие температуры, агрессивные среды) условиях реального производства, а с другими (модельными) веществами в условиях, отличающихся от промышленных.

Одним из основных понятий теории подобия является подобный процесс. Два технологических процесса считаются подобными при совместном соблюдении геометрического и временного подобия, подобия физических величин, а также подобия начальных и граничных условий. Иными словами, если процессы описываются одними дифференциальными уравнениями и имеют одни и те же условия однозначности, то они подобны.

Сформулируем условия подобия на примере подобного движения вязкой жидкости в производственном (I) и в меньшем по размеру лабораторном трубопроводе (II). Для этого рассмотрим любые сходственные точки лежащие, например, на оси труб: А₀^’ и А₀^” (на входе), а также А₁^’ и А₁^”,А₂^’ и А₂^” и т. д. (рис. 2.18).

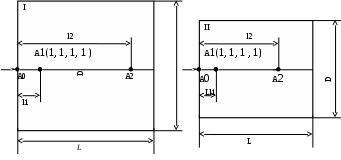Рис. 2.18. К формулировке условий подобия потоков в трубопроводах

Геометрическое подобие соблюдается при равенстве отношений всех сходственных линейных размеров трубопроводов (аппаратов)

,

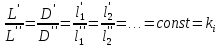(2.170)

где 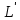и 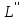- длина трубопроводов; 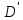и 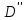диаметры трубопроводов; 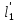, 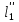и 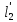, 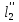и т. д. – пути, проходимые сходственными частицами жидкости от входа до произвольной точки, сходственной для трубопроводов.

Для аппаратов должно соблюдаться геометрическое подобие высот, длин, диаметров и других сходственных размеров.

При подобном движении сходственных частиц их траектории в трубопроводах и аппаратах также должны быть подобны. Это условие иногда называют кинематическим подобием.

Временное подобие характеризуется тем, что сходственные частицы в геометрически подобных системах проходят геометрически подобные пути за промежутки времени, отношение которых является постоянной величиной, то есть

,

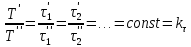(2.171)

где 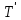и 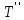- время прохождения сходственными частицами всего трубопровода (первого и второго, соответственно); 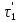, 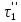и 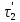, 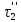и т. д. – время прохождения сходственными частицами путе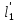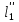й , и 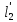, 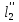и т. д; 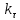- константа временного подобия.

Временное подобие заключается также в том, что сохраняется постоянное отношение между интервалами времени завершения аналогичных стадий процессов в отдельных аппаратах. Например, продолжительность нагрева смеси до температуры кипения в первом аппарате составляет 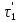, а во втором - 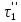. Продолжительность испарения определенного количества воды составляет соответственно 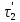и 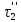. Тогда временное подобие этих процессов будет характеризоваться тем же соотношением (2.171).

При соблюдении геометрического и временного подобия будет соблюдаться также подобие скоростей

(2.172)

Подобие физических величин предполагает, что для любых сходственных точек трубопроводов или аппаратов, размещенных подобно в пространстве и во времени (т. е. при соблюдении геометрического и временного подобия), отношения физических свойств являются величинами постоянными. Так, например, если движущиеся по трубопроводам (рис. 2.18) или аппаратам жидкости имеют вязкость , плотность  и т. д, то для их сходственных точек

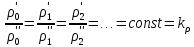	(2.173)
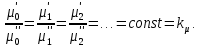	(2.174)

Подобие начальных и граничных условий предполагает, что отношения основных параметров в начальный момент процесса и на границах трубопроводов или аппаратов являются величинами постоянными. Иными словами, для начальных и граничных условий должно соблюдаться геометрическое, временное и физическое подобие, как и для других сходственных точек трубопровода или аппарата.

Константы подобия, входящие в уравнения (2.170)-(2.174) являются постоянными для сходственных точек двух подобных систем, но изменяются в зависимости от соотношения линейных размеров трубопроводов или аппаратов. Константы подобия обладают двумя важными свойствами.

Во-первых, входящие в них одноименные величины могут взаимозаменяться. Поэтому отношения приращений этих величин можно заменять отношениями самих величин, например

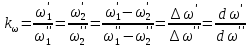(2.175)

Аналогичные выражения можно написать и для уравнений (2.170), (2.171), (2.173) и (2.174).

Во-вторых, коэффициенты подобия с помощью входящих в них величин можно превратить в инварианты подобия. Для этого все подобные величины выражают в относительных единицах, то есть в виде отношений сходственных величин в пределах каждой системы. Так, из уравнения (2.170) следует

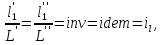(2.176)

причем inv и idem означают инвариантно или "одно и тоже". Величина 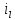представляет собой инвариант подобия геометрических величин.

При выражении любой величины в относительных единицах в качестве масштаба ее измерения может быть выбрано значение этой величины в любой точке системы. Кроме того, в выражении (2.176) вместо длины труб в качестве масштаба можно принять их диаметры.

Аналогично из выражений (2.171)-(2.174) следует

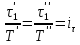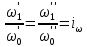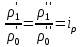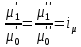(2.177)

В трех последних выражениях за масштаб переменных приняты их значения на входе в систему, т. е. начальные значения.

Представленные инварианты подобия выражены через отношения двух однородных физических величин (параметров). Такие инварианты называют параметрическими критериями или симплексами. Однако инварианты подобия могут быть выражены отношениями разнородных величин, то есть представлять собой безразмерные комплексы этих величин. Например, для сходственных точек подобных потоков жидкостей в трубопроводах таким комплексом является

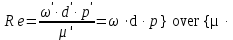(2.178)

Если инварианты подобия выражаются комплексами величин, полученными преобразованием дифференциальных уравнений, описывающих процесс, то их называют критериями подобия. Выражение (2.178) называется критерием Рейнольдса. Критерии подобия всегда имеют физический смысл, являясь мерами соотношения между какими-то двумя эффектами (чаще силами), существенными для рассматриваемого процесса.

Важно отметить, что инварианты и критерии подобия не зависят от относительных размеров объектов и являются безразмерными, то есть не зависят от применяемой системы единиц.

Если критерии подобия составлены только из величин, входящих в условия однозначности, то они являются определяющими. Если в критерии подобия включены еще и другие величины, то критерии называются определяемыми. Теория подобия оперирует критериями подобия обоих видов. Ее основу составляют три теоремы подобия.

Первая теорема подобия была сформулирована Ньютоном: при подобии систем всегда могут быть найдены такие безразмерные комплексы величин, которые для сходственных точек данных систем одинаковы.

Эти безразмерные комплексы, названные критериями подобия легко найти из дифференциальных уравнений, описывающих процесс, деля одну часть уравнения на другую и отбрасывая все знаки операторов. Например, из второго закона Ньютона можно получить критерий Ньютона:



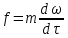
или

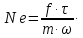(2.179)

Физический смысл критерия Ньютона состоит в том, что он характеризует отношение действующей на частицу силы к силе инерции.

В случае, когда дифференциальные уравнения входят производные высших порядков, также действует правило отбрасывания операторов, например:

,

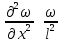(2.180)

где 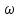– пространственная координата; 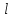– характерный линейный размер по координатной оси .

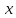Первая теорема указывает также, какие величины следует измерять при проведении опытов, результаты которых требуется обобщить: надо измерять те величины, которые входят в критерии подобия.

Вторая теорема подобия (теорема Бэкингема-Федермана) доказывает, что решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде зависимости между безразмерными комплексами этих величин, то есть между критериями подобия.

Если обозначить критерии подобия через 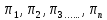то решение дифференциального уравнения может быть представлено в общем виде:

.

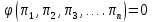(2.181)

Такие уравнения называют критериальными уравнениями. Следовательно, вторая теорема подобия отвечает на вопрос, как обрабатывать результаты опытов: их надо представлять в виде функциональной зависимости между критериями подобия.

Третья теорема подобия (теорема М.В. Кирпичева, А.А. Гухмана) формулирует необходимые и достаточные условия подобия явлений: подобны те явления, которые описываются одной и той же дифференциальных уравнений и у которых соблюдается подобие условий однозначности. Иными словами, явления подобны, если их определяющие критерии равны.

Таким образом, основываясь на теоремах подобия, исследование процессов методами теории подобия должно состоять из следующих этапов:

1) получив полное математическое описание процесса, то есть, составив дифференциальное уравнение и установив условия однозначности, проводят подобное преобразование этого уравнения и находят критерии подобия;

2) опытным путем устанавливают конкретный вид зависимости между критериями подобия, причем полученное обобщенное расчетное уравнение справедливо для всех подобных явлений в исследованных пределах изменения определяющих критериев подобия.