ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
2.7. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ НАВЬЕ–СТОКСА |
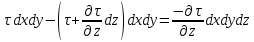 | (2.121) |
Воспользуемся для первой части этого выражения законом внутреннего трения Ньютона (2.14). Тогда
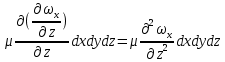 | (2.122) |
Если рассматривать поток в трёхмерном пространстве, то составляющая скорости
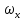 будет изменяться в направлении всех трёх осей и проекция равнодействующей сил трения на ось OX составит:
будет изменяться в направлении всех трёх осей и проекция равнодействующей сил трения на ось OX составит: 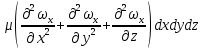 | (2.123) |
Сумму вторых производных по осям координат называют оператором Лапласа и обозначают
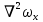 . Следовательно, проекции равнодействующих сил трения на оси равны:
. Следовательно, проекции равнодействующих сил трения на оси равны:| на ось ОХ | 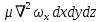 | (2.124) |
| на ось ОУ | 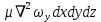 | (2.125) |
| и на ось ОZ | 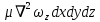 | (2.126) |
Проекции на оси равнодействующих всех сил находятся путём добавления проекций сил тяжести и давления в форме, представленной при выводе уравнения Эйлера (2.113) – (2.115). Для отдельных осей получим:
| для оси ОХ | 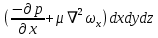 | (2.127) |
| для оси ОУ | 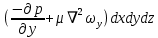 | (2.128) |
| и для оси ОZ | 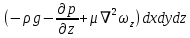 | (2.129) |
Суммы проекций сил на каждую ось, в соответствии с основным принципом динамики, должны быть равны произведению массы жидкости
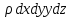 , заключенной в параллелепипеде, на проекцию ускорения на эту ось (
, заключенной в параллелепипеде, на проекцию ускорения на эту ось (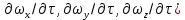 . Приравнивая указанные величины и проводя сокращения имеем:
. Приравнивая указанные величины и проводя сокращения имеем: 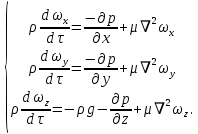 | (2.130) |
В левой части этих выражений, как и в уравнениях Эйлера, присутствуют субстанциональные производные для установившегося и неустановившегося потока, описываемые системами уравнений (2.119) и (2.120).
Система (2.130) называется уравнениями Навье – Стокса, описывающими движение вязкой капельной жидкости.
При движении упругих жидкостей (газов) в них дополнительно возникают, вызванные трением, силы сжатия и растяжения, которые примерно равномерно распределены по осям, поэтому уравнения Навье – Стокса принимают вид:
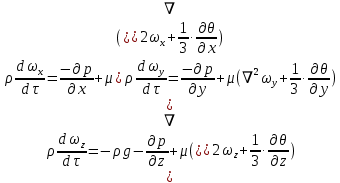 | (2.131) |
где частные производные величины
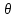 выражают изменение скорости по осям, вызванные действием сил растяжения и сжатия, причем:
выражают изменение скорости по осям, вызванные действием сил растяжения и сжатия, причем: 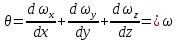 | (2.132) |
В левых частях уравнений Навье – Стокса (2.130) представлены произведения массы единицы объема жидкости на проекцию её ускорения, то есть равнодействующей сил инерции движущейся жидкости по отдельным осям. Произведение
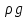 отражает влияние силы тяжести. Частые производные величины
отражает влияние силы тяжести. Частые производные величины 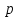 по разным координатам характеризуют изменение гидростатического давления. Произведение вязкости на оператор Лапласа отражает влияние сил трения на движущуюся жидкость. Каждый член уравнений (2.130) имеет размерность силы, отнесенной к единице объема жидкости.
по разным координатам характеризуют изменение гидростатического давления. Произведение вязкости на оператор Лапласа отражает влияние сил трения на движущуюся жидкость. Каждый член уравнений (2.130) имеет размерность силы, отнесенной к единице объема жидкости.Полное описания движения вязкой жидкости получается путем решения уравнений Навье – Стокса совместно с уравнением сплошности потока, что невозможно на данном этапе развития науки. Решения этой сложной системы уравнений получены только для некоторых частных случаев. Так, для установившегося ламинарного движения жидкости решение уравнений Навье – Стокса позволяет получить уравнение Пуазейля (2.89), которое было выведено ранее другим способом.
В важных для промышленной практики случаях применение уравнений Навье – Стокса становится возможным в результате принятия ряда упрощающих допущений (моделирования) или после преобразования этих уравнений методами теории подобия. При движении идеальной жидкости
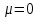 и уравнения Навье – Стокса (2.130) превращаются в уравнения движения Эйлера. Поэтому уравнения Эйлера (2.118) можно рассматривать как частный случай уравнений Навье – Стокса и для них можно найти точное аналитическое решение.
и уравнения Навье – Стокса (2.130) превращаются в уравнения движения Эйлера. Поэтому уравнения Эйлера (2.118) можно рассматривать как частный случай уравнений Навье – Стокса и для них можно найти точное аналитическое решение.
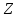 до горизонтальной плоскости отсчета (рис.2.14).
до горизонтальной плоскости отсчета (рис.2.14).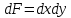 .
.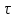 , а на верхней грани оно составляет
, а на верхней грани оно составляет 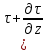 dz).
dz).