ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
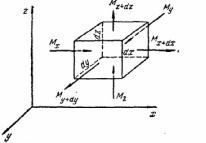
2.5. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ ПОТОКАЕсли поток жидкости сплошной или неразрывный, то есть не образует пустот, не заполненных жидкостью, то для него можно установить общую зависимость между скоростями. Для этого выделим в потоке жидкости элементарный параллелепипед объемом 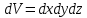 , ребра которого параллельны осям координат (рис. 2.12). , ребра которого параллельны осям координат (рис. 2.12).Пусть проекция скорости на ось ОХ во всех точках левой грани составляет 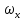 , а площадь этой грани , а площадь этой грани 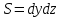 . Тогда, согласно выражению (2.67), через эту грань в параллелепипед вдоль оси ОХ в единицу времени войдет масса жидкости . Тогда, согласно выражению (2.67), через эту грань в параллелепипед вдоль оси ОХ в единицу времени войдет масса жидкости 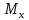 , равная , равная 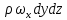 , а за время , а за время 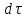 – масса жидкости – масса жидкости
где 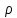 – плотность жидкости на левой грани параллелепипеда. – плотность жидкости на левой грани параллелепипеда.
Примем, что скорость и плотность жидкости на противоположной грани отличаются от соответствующих величин на левой грани и составляют 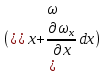 и и 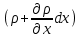 . Тогда через правую грань параллелепипеда за то же время . Тогда через правую грань параллелепипеда за то же время 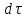 выйдет масса жидкости выйдет масса жидкости
Приращение массы жидкости в параллелепипеде вдоль оси ОХ составит:
Обозначим проекции скоростей на оси ОY и OZво всех точках задней и нижней граней 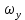 и и 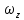 , тогда приращения массы жидкости в параллелепипеде вдоль этих осей составляет: , тогда приращения массы жидкости в параллелепипеде вдоль этих осей составляет:
и
Общее накопление жидкости в параллелепипеде 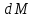 за время за время 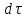 равно сумме выражений (2.96) – (2.98). равно сумме выражений (2.96) – (2.98).
Однако, накопление жидкости в параллелепипеде, заполненном жидкостью возможно только в результате изменения плотности жидкости в этом объеме, поэтому
Приравнивая два последних выражения, проводя сокращения и перенося все слагаемые в левую часть равенства, получаем дифференциальное уравнение неразрывности потока для неустановившегося движения сжимаемой жидкости
Если произведение 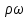 продифференцировать как сложную функцию, то это уравнение можно представить в несколько ином виде продифференцировать как сложную функцию, то это уравнение можно представить в несколько ином виде
или после деления этого уравнения на 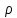
где 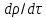 – субстанциональная производная плотности. – субстанциональная производная плотности. Для установившегося потока в уравнении неразрывности потока (2.101) 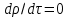 и оно имеет вид: и оно имеет вид:
которое является уравнением неразрывности потока несжимаемой жидкости. Слагаемые в левой части называются дивергенцией вектора скорости, поэтому уравнение (2.104) можно представить как
Для того, чтобы перейти от элементарного ко всему объему жидкости надо проинтегрировать уравнение (2.103). Если площадь сечения трубопровода не изменяется, а поток движется в установившемся режиме вдоль одной оси (например ОХ), то результат интегрирования при  составляет составляет
Если площадь сечения трубопровода 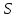 переменна, то интегрирование также по ней даёт переменна, то интегрирование также по ней даёт
 Рис. 2.13 Трубопровод переменного сечения. Для трех различных сечений (1-1, 2-2, 3-3) трубопровода (рис. 2.13) имеем
или
где 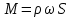 – массовый расход жидкости, – массовый расход жидкости,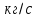 . .Выражения (2.107) – (2.109) являются интегральной формой уравнения сплошности потока или уравнением постоянства расхода. Согласно им: при установившемся движении жидкости, полностью заполняющей трубопровод, через каждое его конкретное сечение в единицу времени проходит одно и то же количество жидкости. Поскольку для капельных жидкостей 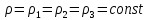 , то выражения (2.107) и (2.108) приобретают вид , то выражения (2.107) и (2.108) приобретают вид
или
где 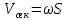 – объемный расход жидкости, – объемный расход жидкости, 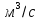 . . Уравнение постоянства расхода в форме выражения (2.109) является частным случаем закона сохранения массы и выражает материальный баланс потока. В некоторых случаях, например при вскипании жидкости за счет резкого понижения давления в насосах, образуется пар, который разрывает поток жидкости, поэтому уравнение сплошности потока не выполняется. | ||||||||||||||||||||||||||||||||||||||||||

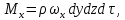
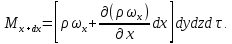
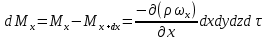 .
.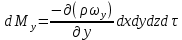
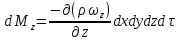 .
.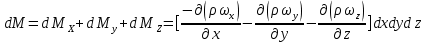
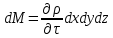
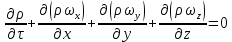
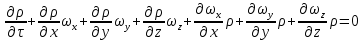
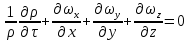
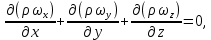
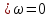
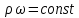
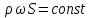
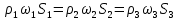
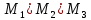
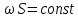 ,
,