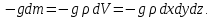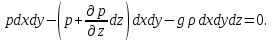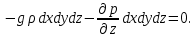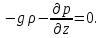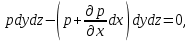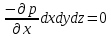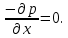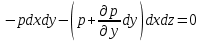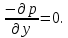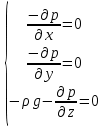ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
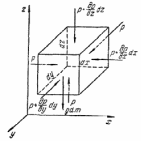
2.2. ГИДРОСТАТИКА. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ РАВНОВЕСИЯ ЭЙЛЕРАГидростатика изучает равновесия жидкостей, находящихся в состоянии относительного покоя, при котором в движущейся жидкости её частицы не перемещаются друг относительно друга. В этом случае силы внутреннего трения отсутствуют, то есть жидкость является идеальной. В состоянии относительного покоя форма объёма жидкости не изменяется и она, подобно твёрдому телу, перемещается как единое целое. Таким образом, жидкость находится в состоянии покоя относительно стенок сосуда, например, в движущейся цистерне или в барабане центрифуги, вращающемся с постоянной скоростью. Если не только жидкость находится в покое относительно стенок сосуда, но и сам сосуд неподвижен относительно поверхности земли, то наблюдается состояние абсолютного равновесия, которое является частным случаем относительного равновесия. В состоянии любого покоя на жидкость действуют силы тяжести и давления. В состоянии относительного покоя следует также учитывать силу инерции, вызывающую движение жидкости вместе с сосудом с постоянной скоростью. Соотношение между силами, действующими на жидкость в состоянии покоя, называется условием равновесия и выражается дифференциальными уравнениями равновесия Эйлера. Выделим в объёме находящейся в абсолютном покое жидкости элементарный параллелепипед массой 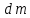 и объёмом и объёмом 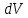 , с рёбрами , с рёбрами 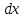 , , 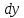 и и 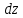 , расположенными параллельно осям , расположенными параллельно осям 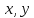 и и 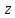 (рис. 2.2). Сила тяжести, действующая на параллелепипед, составляет (рис. 2.2). Сила тяжести, действующая на параллелепипед, составляет 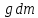 . .Сила гидростатического давления на каждую грань параллелепипеда равна произведению давления 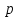 на площадь грани. Пусть давление является функцией всех координат: на площадь грани. Пусть давление является функцией всех координат: 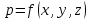 Выясним вид этой функции, т. е. распределение гидростатического давления по объёму жидкости, что является основной задачей гидростатики. Выясним вид этой функции, т. е. распределение гидростатического давления по объёму жидкости, что является основной задачей гидростатики.Согласно основному принципу гидростатики: сумма проекций на оси координат всех сил, действующих на элементарный объём, находящийся в равновесии, равна нулю. Если этот принцип не выполняется, то происходит движение.
Рассмотрим сумму проекций сил на ось 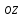 . Сила тяжесть направлена параллельно оси и имеет отрицательную проекцию: . Сила тяжесть направлена параллельно оси и имеет отрицательную проекцию:
Сила гидростатического давления на нижнюю грань параллелепипеда направлена параллельно оси и её проекция составляет 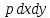 . Если изменение гидростатического давления в данной точке в направлении оси . Если изменение гидростатического давления в данной точке в направлении оси 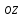 равно равно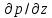 , то на верхней грани параллелепипеда это изменение по сравнению с нижней гранью составит , то на верхней грани параллелепипеда это изменение по сравнению с нижней гранью составит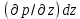 . Тогда сила гидростатического давления на верхнюю грань будет иметь отрицательную проекцию по оси . Тогда сила гидростатического давления на верхнюю грань будет иметь отрицательную проекцию по оси 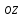 и составлять и составлять 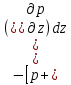 . .Проекции всех сил на ось 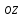 имеют вид: имеют вид:
После преобразований получаем:
Выделенный объём 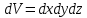 не может быть равным нулю, поэтому получаем: не может быть равным нулю, поэтому получаем:
Сумма проекций сил на ось 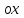
откуда после сокращений получаем:
или
Аналогично для оси 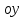
или после преобразований
Таким образом, условия равновесия элементарного параллелепипеда выражаются системой уравнений:
Система уравнений (2.29) называется дифференциальными уравнениями равновесия Эйлера. Для получения закона распределения давления во всём объёме покоящейся жидкости, надо проинтегрировать систему (2.29). Результатом интегрирования является основное уравнение гидростатики, широко используемое в инженерных расчётах. |