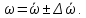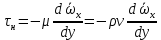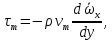ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
2.4. ГИДРОДИНАМИКА. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ ЖИДКОСТЕЙНарушение равновесия, т. е. движение жидкости, может происходить под действием движущей силы – разности давлений, создаваемой насосами или компрессорами, разности уровней жидкости или разности плотностей. Знание законов гидродинамики позволяет находить разность давлений, необходимую для перемещения данного количества жидкости с требуемой скоростью, а значит и расход энергии на это перемещение, а также решать обратную задачу – определять скорость и расход жидкости при известном перепаде давления. Гидродинамика решает внутреннюю и внешнюю задачи. Внутренняя задача связана с анализом движения жидкостей внутри труб и каналов, а ее решения позволяют проводить инженерные расчеты трубопроводов. Внешняя задача заключается в установлении закономерностей обтекания жидкостями твердых частиц при перемешивании, осаждении и так далее. Во многих случаях жидкости движутся через зернистый слой твердого материала внутри каналов сложной формы и одновременно обтекают твердые частицы. Такие условия наблюдаются в процессах фильтрования, химических реакциях с катализаторами и других. В таких случаях приходится решать смешанную гидродинамическую задачу. Ее решение сводят к решению внешней или внутренней задачи. Движущей силой большинства процессов в биотехнологических производствах является разность давлений. Тогда основное кинетическое уравнение движения запишется в виде:
где V – объем перемещаемой жидкости, м3; F – площадь поперечного сечения, через которое протекает жидкость, м2; - продолжительность процесса движения жидкости, с; R – сопротивление протеканию жидкости; p – разность давлений. Величина dV/d является объемным расходом жидкости Vсек. Объемный расход жидкости, отнесенный к площади поперечного сечения потока F, называется средней фиктивной скоростью
Ее введение связано с тем, что истинная скорость движения жидкости изменяется по диаметру потока от оси к стенке трубопровода или канала, и закон распределения скоростей часто неизвестен. Массовый расход жидкости М (кг/с) определяется произведением
где - плотность перемещаемой жидкости. Значит, массовая скорость движения жидкости W составляет:
Соотношения (2.59)-(2.62) выполняются при движении жидкости по трубопроводам или каналам с сечением любой формы. Если жидкость движется через сечение отличное от круглой формы, то в качестве расчетного линейного размера принимают гидравлический радиус или эквивалентный диаметр. Под гидравлическим радиусом rг понимают отношение площади свободного сечения трубопровода или канала, через которое протекает жидкость, к смоченному периметру
где S – площадь сечения потока жидкости; П – смоченный периметр. Для круглой трубы с внутренним диаметром d и, значит, площадью свободного сечения S = πd2/4 при сплошном заполнении его жидкостью П = πd, гидравлический радиус составит:
Следовательно, эквивалентный диаметр составляет:
Эквивалентный диаметр равен диаметру гипотетического трубопровода круглого сечения, для которого отношение площади к смоченному периметру то же, что и для трубопровода некруглого сечения. Различают установившееся и неустановившееся движения жидкости. При установившемся движении скорости, ускорения частиц жидкости, давления и другие характеристики не изменяются во времени, а являются только функцией координат, т. е. зависят лишь от положения рассматриваемой точки в потоке
При неустановившемся движении скорость, давление и другие характеристики движения жидкости являются функциями не только координат, но и времени τ
Установившееся движение характерно для непрерывных процессов, а неустановившееся движение наблюдается в периодических процессах. Установившееся движение может быть равномерным и неравномерным. Равномерное движение характеризуется неизменностью скорости, давления, формы потока и других величин по длине потока. Примером равномерного движения является движение жидкости в трубопроводе постоянного сечения с постоянной скоростью. Давление и другие величины изменяются по длине потока. Неравномерное движение происходит, например, в конической трубе, когда скорость, давление и глубина потока изменяются по длине трубы. Проводя различие между установившемся и неустановившемся движением жидкости в виде частной производной (например, скорости 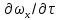 ), рассматривают изменение параметра в фиксированной точке с постоянными координатами. Однако, для каждой частицы движущейся жидкости изменение ее параметров во времени и в пространстве выражается не частной, а полной производной по времени. В гидравлике ее называют субстанциональной производной. По физическому смыслу эта производная является следующей за потоком. ), рассматривают изменение параметра в фиксированной точке с постоянными координатами. Однако, для каждой частицы движущейся жидкости изменение ее параметров во времени и в пространстве выражается не частной, а полной производной по времени. В гидравлике ее называют субстанциональной производной. По физическому смыслу эта производная является следующей за потоком.Любой параметр или свойство U (скорость, плотность, давление и т. д.), изменяющееся в потоке в пространстве и во времени, называется субстанцией. Пусть мы наблюдаем за движением потока и можем мгновенно регистрировать значение U в каждый момент времени в данной точке потока. Если наблюдатель неподвижен, то изменение U в единицу времени в фиксированной точке пространства (x, y, z) = const выражается частной производной 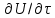 , а изменение величины U за бесконечно малый промежуток времени , а изменение величины U за бесконечно малый промежуток времени 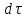 составит ( составит (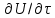 ) )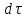 . Эта величина является местным или локальным изменением, которое при установившемся потоке равно нулю. . Эта величина является местным или локальным изменением, которое при установившемся потоке равно нулю.Если наблюдатель перемещается вместе с частицей потока, то измеряя U, можно установить, что изменение этой величины состоит из двух частей. Пусть за время 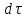 частица жидкости из точки А (x, y, z) переместилась в точку B с координатами (x + dx), (y + dy) и (z + dz). За счет этого перемещения величина U изменилась на частица жидкости из точки А (x, y, z) переместилась в точку B с координатами (x + dx), (y + dy) и (z + dz). За счет этого перемещения величина U изменилась на
причем это изменение не связано с изменением U во времени в какой – либо фиксированной точке пространства, т. е. оно соответствует установившемуся потоку. Выражение (2.68) характеризует конвективное, связанное с перемещением, изменение параметра U. Поскольку движение жидкости неустановившееся, то за это время 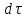 величина U в каждой точке пространства изменится на величину величина U в каждой точке пространства изменится на величину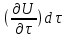 . Значит, полное изменение величины U при неустановившемся движении будет представлять сумму локального и конвективного изменений . Значит, полное изменение величины U при неустановившемся движении будет представлять сумму локального и конвективного изменений
Разделим обе части этого выражения на 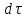 , то есть определим мгновенное изменение U, а так же, учитывая, что , то есть определим мгновенное изменение U, а так же, учитывая, что
где ωx , ωy и ωz - составляющие скорости вдоль соответствующих осей координат, на которые можно разложить скорость ω, получим:
В случае установившегося процесса в этом выражении 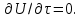 Следует учесть, что в субстанциональной производной (2.71) заложен тот факт, что при движении частицы жидкости со скоростью ω конвективное и локальное изменения претерпевают все составляющие скорости вдоль осей координат (ωx , ωy и ωz). Для каждой из этих составляющих полные производные имеют вид аналогичный выражению (2.71), а производные 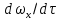 , , 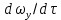 , , 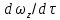 характеризуют составляющие ускорения вдоль соответствующих осей координат. характеризуют составляющие ускорения вдоль соответствующих осей координат.Режимы движения потоков жидкостей также подразделяют по траекториям движения их частиц. По этому признаку различные режимы движения жидкости можно визуально наблюдать, вводя в поток подкрашенную струйку жидкости или индикатор. При небольшой скорости потока жидкости окрашенная струйка вытягивается в нить, которая, не размываясь, достигает конца трубы. Это свидетельствует о том, что траектории частиц прямолинейны и параллельны друг другу. Движение, при котором все частицы жидкости движутся по параллельным траекториям, называется струйчатым или ламинарным. Если скорость жидкости увеличить сверх определенного предела, то окрашенная струйка приобретает сначала волнообразные движения, а затем начинает размываться, смешиваясь с основной массой жидкости. Это вызвано тем, что отдельные частицы жидкости движутся уже не параллельно друг другу и оси трубы, а в поперечном направлении. Неупорядоченное движение, при котором отдельные частицы жидкости двигаются по запутанным, хаотическим траекториям, а масса жидкости в целом перемещается в одном направлении, называется турбулентным движением. В турбулентном потоке происходят пульсации скоростей, под действием которых частицы жидкости получают перемещение не только в главном (осевом) направлении, но и в поперечном, вызывающем интенсивное перемешивание потока по сечению, что ведет к более высоким энергозатратам на движение, чем при ламинарном потоке. Из опытных данных установлено, что переход от ламинарного к турбулентному режиму движения происходит тем легче, чем больше массовая скорость жидкости 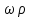 и диаметр трубы d и чем меньше вязкость μ жидкости. Эти величины можно объединить в безразмерный комплекс Re, который в честь разработчика назван критерием Рейнольдса и диаметр трубы d и чем меньше вязкость μ жидкости. Эти величины можно объединить в безразмерный комплекс Re, который в честь разработчика назван критерием Рейнольдса
Критерий Re является мерой соотношения между силами вязкости и инерции. Действительно, переход от упорядоченного ламинарного движения к хаотическому турбулентному тем легче, чем меньше вязкость, препятствующая этому, и чем больше плотность, являющаяся мерой инерции уже отклонившихся от прямолинейного движения частиц. Кроме того перемешивание возникает легче при более высокой скорости и в большем пространстве, т. е. при большем диаметре. Критерий Re введен для того, чтобы каждый раз не определять режим движения опытным путем. Установлено, что движение по гладким трубам при Re < 2320 является ламинарным. При 10000 > Re ≥ 2320 режим является переходным (смешанным), то есть может быть как ламинарным, так и турбулентным. Если Re≥10000 режим движения становится устойчивым турбулентным. Указанные значения Re являются условными. Они соответствуют капельным жидкостям по свойствам близким к воде в условиях стабилизированного изотермического потока. Нарушение этих условий или наличие возмущений, вызванных шероховатостью труб, изменением скорости потока по величине или направлению и так далее, изменяют значение Re, соответствующие различным режимам движения жидкостей. Кроме того, поскольку плотность газов на 3, а вязкость на 1,5-2,0 порядка ниже, чем у капельных жидкостей, то и значения критериев Re, соответствующие различным режимам движения, для них будут иные. В случае движения жидкости по трубам некруглого сечения при расчете критерия Re по выражению (2.72) вместо d используют эквивалентный диаметр, определяемый по формуле (2.65). Для вычисления критерия Re используют среднюю скорость потока ω. Действительные же скорости жидкости не одинаковы в разных точках сечения трубопровода. Распределение этих скоростей по сечению потока различно для ламинарного и турбулентного движения. Для ламинарного потока вид распределения скоростей может быть установлен теоретически. Для этого поток вязкой жидкости, ламинарно движущейся по прямой трубе круглого сечения, мысленно разобьем на ряд кольцевых слоев (рис. 2.9, а) соосных с трубой.
В результате действия сил трения, слои будут двигаться с разными скоростями. Центральный цилиндрический слой у оси трубы имеет максимальную скорость, но по мере удаления от оси, скорость слоев уменьшается. У самой стенки скорость жидкости обращается в нуль. Выделим в потоке жидкости, движущейся по трубе радиусом R (рис. 2.9, б), цилиндрический слой длинной l и радиусом r. Движение этого слоя происходит под действием разности сил давления P1 и P2, приложенных к торцевым сторонам цилиндра:
где p1 и p2 – гидростатическое давление в сечениях 1–1 и 2–2. Движению цилиндра оказывает сопротивление сила внутреннего трения T, которая согласно (2.13) равна
где 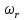 – скорость движения жидкости вдоль оси цилиндра на расстоянии r от оси; F = 2πrl – наружная поверхность цилиндра. Знак минус показывает, что скорость убывает с увеличением радиуса цилиндра, а при r = Rзначение – скорость движения жидкости вдоль оси цилиндра на расстоянии r от оси; F = 2πrl – наружная поверхность цилиндра. Знак минус показывает, что скорость убывает с увеличением радиуса цилиндра, а при r = Rзначение 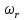 становится равно нулю. становится равно нулю.При установившемся движении силы
откуда после сокращения и разделения переменных:
Чтобы перейти ко всему объему жидкости в трубе, интегрируем это выражение, учитывая изменение радиуса цилиндра от r до R и скорости жидкости от 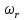 до 0. В итоге получаем: до 0. В итоге получаем:
Из выражения (2.77) видно, что скорость имеет максимальное значение на оси трубы, где r = 0.
Сопоставляя два последних выражения можно найти скорость на любом расстоянии от оси трубы
Данная формула является законом Стокса, отражающим параболическое распределение скорости в сечении трубы при ламинарном течении. Для определения обычного расхода жидкости при ламинарном ее движении рассмотрим элементарное кольцевое сечение (рис. 2.9, б) с внутренним радиусом r и внешним радиусом r + dr, площадь сечения которого равна dS = 2πrdr. Объемный расход жидкости через это сечение составляет:
а с учетом уравнения (2.77):
Интегрируя это выражение в интервале изменения r от 0 до R, получим общий расход жидкости через трубу:
Подставляя вместо R диаметр трубы d = 2R и обозначая p1 – p2 = 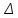 p, окончательно получаем уравнение Пуазейля, определяющее расход жидкости при ее ламинарном движении по круглой прямой трубе p, окончательно получаем уравнение Пуазейля, определяющее расход жидкости при ее ламинарном движении по круглой прямой трубе
Соотношение между средней скоростью и максимальной можно получить, приравняв выражения (2.60) и (2.82), т. е 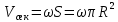 и тогда и тогда
откуда
Сравнивая эту среднюю скорость с выражением (2.78), находим
Таким образом, при ламинарном потоке в трубе средняя скорость жидкости равна половине скорости по оси трубы, а параболический закон распределения скоростей с учетом выражения (2.86) можно представить формулой
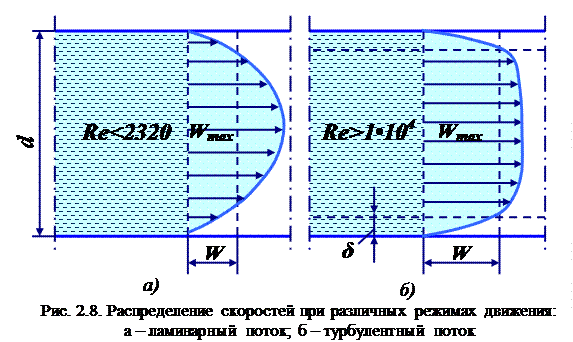
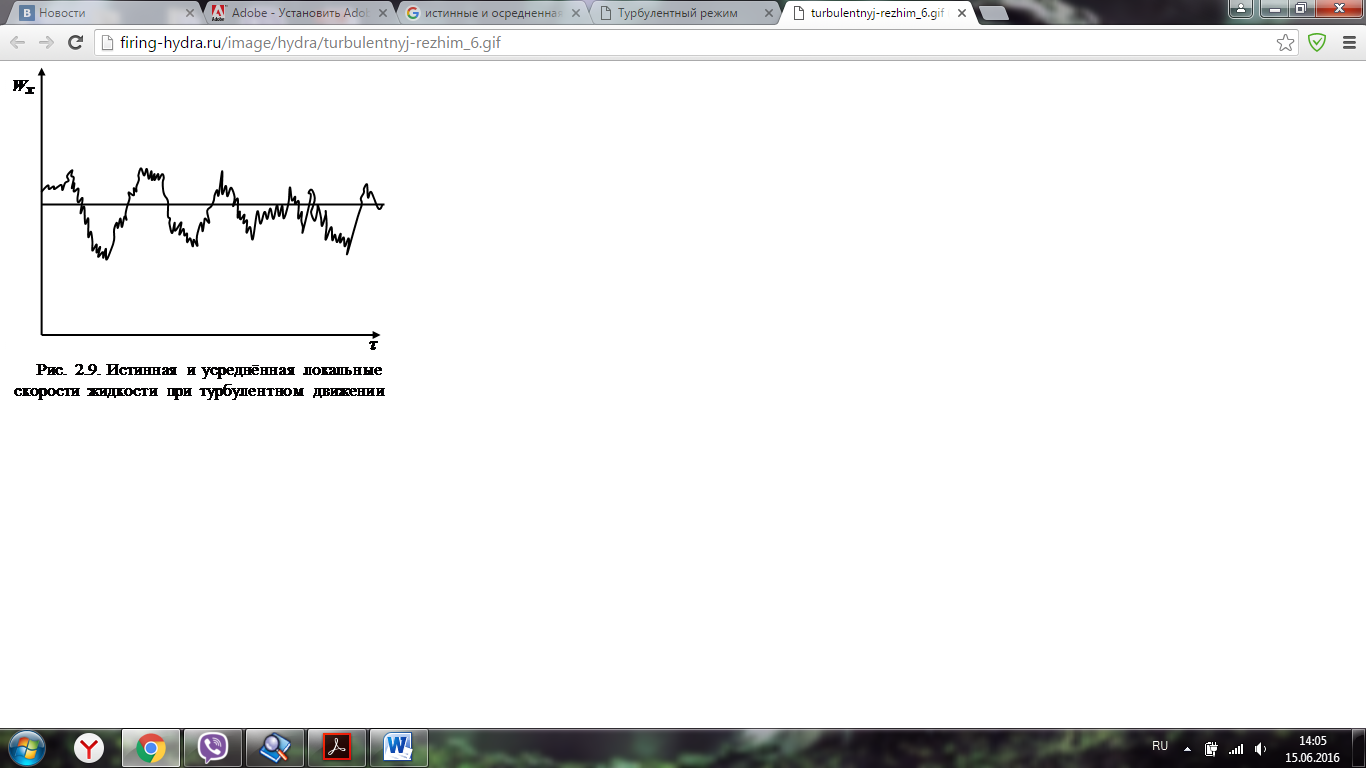
Этот закон, полученный теоретически, хорошо подтверждается экспериментально полученными эпюрами скоростей (рис.2.10, а). На практике чаще приходится иметь дело с турбулентным движением, для которого из-за хаотического движения частиц распределение скоростей по сечению потока отличается от параболического (рис. 2.10, б), происходит выравнивание скоростей и кривая их распределения имеет значительно более широкую вершину. Средняя скорость при турбулентном режиме значительно больше половины максимальной скорости и зависит от значения Re. Например, при Re равном 1∙104 она составляет 0,8 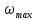 , а для Re равного 1∙108 ее значение 0,9 , а для Re равного 1∙108 ее значение 0,9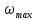 . Для турбулентного движения, являющегося очень сложным, невозможно теоретически получить профиль распределения скоростей (рис. 2.10, б), что выражает распределение не истинных, а осредненных во времени скоростей. Это вызвано тем, что в каждой точке истинная скорость не остается постоянной во времени, поскольку частицы находятся в хаотическом движении. Ее мгновенные значения испытывают флуктуации, то есть нерегулярные изменения (пульсации). В качестве примера на рис. 2.11 представлено изменение истинной мгновенной скорости ωx вдоль оси OX потока в одной точке в зависимости от времени. Видно, что скорости пульсируют около некоторой осредненной во времени величины . Для турбулентного движения, являющегося очень сложным, невозможно теоретически получить профиль распределения скоростей (рис. 2.10, б), что выражает распределение не истинных, а осредненных во времени скоростей. Это вызвано тем, что в каждой точке истинная скорость не остается постоянной во времени, поскольку частицы находятся в хаотическом движении. Ее мгновенные значения испытывают флуктуации, то есть нерегулярные изменения (пульсации). В качестве примера на рис. 2.11 представлено изменение истинной мгновенной скорости ωx вдоль оси OX потока в одной точке в зависимости от времени. Видно, что скорости пульсируют около некоторой осредненной во времени величины 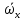 , которая может быть найдена из соотношения: , которая может быть найдена из соотношения:
Таким образом, величина 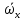 равна высоте прямоугольника, равновеликого площади, заключенной между пульсационной кривой и осью абсцисс в пределах изменения времени от 0 до τ. равна высоте прямоугольника, равновеликого площади, заключенной между пульсационной кривой и осью абсцисс в пределах изменения времени от 0 до τ.Разность между истинной и осредненной скоростями называют мгновенной пульсационной скоростью 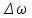 , т. е. , т. е.
Согласно рис. 2.11 величина 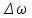 имеет переменный знак, поэтому имеет переменный знак, поэтому
Осредненная скорость принципиально отличается от средней скорости. Осредненная скорость является средней по времени в данной точке. Средняя скорость относится к поперечному сечению в данный момент времени. Осредненная скорость 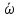 в достаточно большом промежутке времени остается постоянной. Следовательно, турбулентное движение, являющееся неустановившимся, можно считать квазистационарным. в достаточно большом промежутке времени остается постоянной. Следовательно, турбулентное движение, являющееся неустановившимся, можно считать квазистационарным.Мгновенные пульсационные скорости 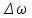 различаются по величине, но вместо них можно использовать среднеквадратичную величину различаются по величине, но вместо них можно использовать среднеквадратичную величину 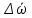 , тогда скорость турбулентного потока в данной точке: , тогда скорость турбулентного потока в данной точке:
Величина 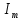 , равная соотношению , равная соотношению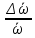 , называется интенсивностью турбулентности, которая является количественной характеристикой пульсаций в данной точке потока. При турбулентном движении жидкостей по трубам , называется интенсивностью турбулентности, которая является количественной характеристикой пульсаций в данной точке потока. При турбулентном движении жидкостей по трубам 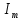 обычно составляет 0,01 – 0,1. Если значения средних пульсаций скорости одинаковы во всех направлениях, то турбулентность называется изотропной. Турбулентность приближается к изотропной вблизи оси потока и все больше отклоняется от нее в поперечном направлении к стенке трубы. обычно составляет 0,01 – 0,1. Если значения средних пульсаций скорости одинаковы во всех направлениях, то турбулентность называется изотропной. Турбулентность приближается к изотропной вблизи оси потока и все больше отклоняется от нее в поперечном направлении к стенке трубы.Другими важными характеристиками турбулентного движения являются масштаб турбулентности и турбулентная вязкость. Близко расположенные в турбулентном потоке частицы имеют мало отличающиеся истинные скорости и движутся совместно. Совокупность этих частиц называется вихрем. Размер вихря зависит от развитости турбулентного потока. Частицы двух различных вихрей существенно отличаются по скоростям и их пульсациям. Минимальное расстояние между двумя частицами, принадлежащим к различным вихрям, называется масштабом турбулентности. Для характеристики турбулентной вязкости рассмотрим две частицы жидкости, движущиеся в турбулентном потоке вдоль оси трубы OX. Пусть расстояние между частицами в направлении перпендикулярном оси составляет dy. Проекции скоростей частиц на ось OX равны 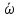 x,1 и x,1 и 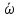 x,2, отличаются на величину d x,2, отличаются на величину d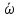 x. Вследствие разности скоростей возникает ньютоновское напряжение x. Вследствие разности скоростей возникает ньютоновское напряжение 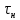 , препятствующее движению частиц , препятствующее движению частиц
Если бы поток был ламинарным, то напряжение 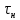 было бы единственным. Однако в турбулентном потоке частицы движутся друг относительно друга и в направлении оси OY, перпендикулярной движению жидкости, что создает дополнительное касательное напряжение было бы единственным. Однако в турбулентном потоке частицы движутся друг относительно друга и в направлении оси OY, перпендикулярной движению жидкости, что создает дополнительное касательное напряжение 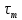 , называемое турбулентным напряжением, которое по аналогии с , называемое турбулентным напряжением, которое по аналогии с 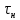 можно выразить уравнением можно выразить уравнением
где 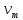 – турбулентная вязкость. Величина – турбулентная вязкость. Величина 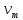 зависит от скорости и от других параметров жидкости (например, расстояния от стенки трубы), определяющих степень турбулентности потока, поэтому, в отличие от величины зависит от скорости и от других параметров жидкости (например, расстояния от стенки трубы), определяющих степень турбулентности потока, поэтому, в отличие от величины 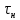 , не является физико-химической константой. , не является физико-химической константой.Исходя из представления о турбулентной вязкости, сечение потока можно представить состоящим из нескольких зон. Центральная зона, составляющая основную массу жидкости, в которой частицы движутся примерно с одинаковыми скоростями, называется ядром потока. В ядре потока движение является развитым турбулентным с преобладанием касательного напряжения 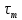 и вязкостью и вязкостью 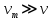 . От границы ядра потока до стенки трубы расположен гидродинамический пограничный слой, в котором скорость жидкости снижается от значения в ядре потока до нуля у стенки трубы. В этом слое можно выделить две зоны. Зона, непосредственно прилегающая к ядру потока, называется переходной зоной. В ней снижение скорости происходит таким образом, что движение жидкости из турбулентного постепенно переходит в ламинарное, а величины . От границы ядра потока до стенки трубы расположен гидродинамический пограничный слой, в котором скорость жидкости снижается от значения в ядре потока до нуля у стенки трубы. В этом слое можно выделить две зоны. Зона, непосредственно прилегающая к ядру потока, называется переходной зоной. В ней снижение скорости происходит таким образом, что движение жидкости из турбулентного постепенно переходит в ламинарное, а величины 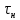 и и 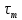 , а также , а также 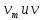 , становятся сравнимыми по порядку. Зона от границы переходной области до стенки трубы δ очень мала. Она составляет несколько десятых долей миллиметра, характеризуется часто ламинарным движением, преобладанием , становятся сравнимыми по порядку. Зона от границы переходной области до стенки трубы δ очень мала. Она составляет несколько десятых долей миллиметра, характеризуется часто ламинарным движением, преобладанием 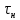 и значением и значением 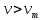 . Эта зона называется ламинарным пограничным или вязким подслоем. В вязком подслое на поверхности стенки скорость движения равна нулю, поскольку твердая стенка «гасит» турбулентные пульсации и слой жидкости как бы прилипает с ней так, что даже ламинарное движение невозможно. . Эта зона называется ламинарным пограничным или вязким подслоем. В вязком подслое на поверхности стенки скорость движения равна нулю, поскольку твердая стенка «гасит» турбулентные пульсации и слой жидкости как бы прилипает с ней так, что даже ламинарное движение невозможно.Представленная модель структуры турбулентного потока является упрощенной, так как четких границ между указанными зонами не существует. Однако, даже из этой модели видно, что турбулентное движение всегда сопровождается ламинарным у твердой границы потока (стенки трубы). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

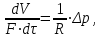
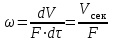 .
.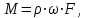
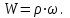
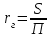
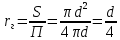 .
.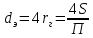 .
.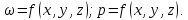
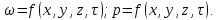
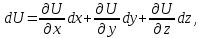
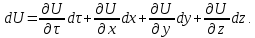
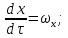
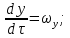
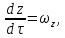
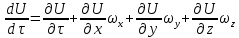
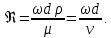

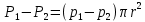 ,
,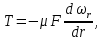
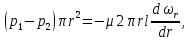
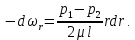
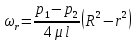 .
.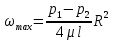 .
.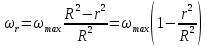 .
.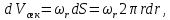
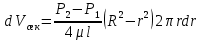 .
.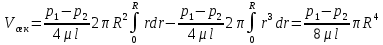 .
.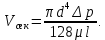
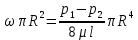 ,
,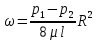 .
.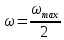
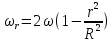 .
.
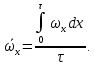
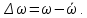
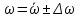 .
.