ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
2.13 ПРИБЛИЖЕННОЕ МОДЕЛИРОВАНИЕ. АВТОМОДЕЛЬНОСТЬПри моделировании многих процессов биотехнологии не соблюдается полное подобие, то есть не выполняется равенство всех определяющих критериев натуры и модели, как это требует третья теорема подобия. Пусть, например, для процесса определяющими являются критерии 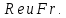 Для натуры они имеют значения Для натуры они имеют значения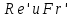 , а для модели , а для модели 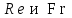 , то есть должны соблюдаться равенства , то есть должны соблюдаться равенства
или в развернутом виде
Примем, что рабочие жидкости в натуре и модели одинаковы, а значит 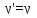 , тогда из выражения (2.208) условиями подобия являются , тогда из выражения (2.208) условиями подобия являются
Это возможно лишь при условии одинаковых размеров модели и натуры 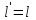 то есть моделирование не возможно. Чтобы такая ситуация не возникала жидкость в натуре и модели должны иметь различную вязкость, тогда то есть моделирование не возможно. Чтобы такая ситуация не возникала жидкость в натуре и модели должны иметь различную вязкость, тогда
откуда
Это означает, что если размеры модели в 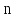 раз меньше натуры, то вязкость жидкости в модели должна быть в раз меньше натуры, то вязкость жидкости в модели должна быть в 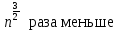 . Например, при использовании в натуре воды, для модели, которая в 4 раза меньше, надо применять жидкость имеющую вязкость в 8 раз меньше, чем у воды, что практически трудно осуществлять имеющую вязкость. . Например, при использовании в натуре воды, для модели, которая в 4 раза меньше, надо применять жидкость имеющую вязкость в 8 раз меньше, чем у воды, что практически трудно осуществлять имеющую вязкость. При количестве определяющих критериев больше двух выполнить условия полного моделирования, то есть удовлетворяются соблюдением не полного подобия, а лишь подобием тех факторов, которые наиболее значительно влияют на исследуемый процесс. Например, анализируя выражение (2.204), мы говорили, что критерий 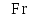 (сила тяжести) может не играть существенной роли. Это возможно, когда турбулентное движение капельной жидкости производят с помощью насосов. В этом случае влияние собственного веса жидкости на распределение скоростей и перепад давления мало. Следовательно, критерий (сила тяжести) может не играть существенной роли. Это возможно, когда турбулентное движение капельной жидкости производят с помощью насосов. В этом случае влияние собственного веса жидкости на распределение скоростей и перепад давления мало. Следовательно, критерий 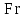 можно исключить из критериального уравнения, которое принимает вид можно исключить из критериального уравнения, которое принимает вид
а его развернутая форма задаётся выражением (2.189). Считается, что процесс является автомодельным по отношению к критерию 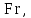 то есть не зависим от него. Автомодельность может возникать и при изменении условий протекания одного процесса. Например, ниже будет показано, что сопротивление сил трения движению вязкой жидкости при низких значениях критерия то есть не зависим от него. Автомодельность может возникать и при изменении условий протекания одного процесса. Например, ниже будет показано, что сопротивление сил трения движению вязкой жидкости при низких значениях критерия 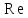 сильно зависит от величины этого критерия и в малой степени от шероховатости стенок трубы. При высоких значениях критерия сильно зависит от величины этого критерия и в малой степени от шероховатости стенок трубы. При высоких значениях критерия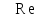 фактором, определяющим сопротивление, становится именно шероховатость. Сопротивление перестаёт зависеть от фактором, определяющим сопротивление, становится именно шероховатость. Сопротивление перестаёт зависеть от 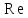 , то есть процесс становится автомодельным по отношению к этому критерию. В случае автомодельности по критерию, его показатель степени в обобщенном уравнении типа (2.203) становится равным или близок к нулю. , то есть процесс становится автомодельным по отношению к этому критерию. В случае автомодельности по критерию, его показатель степени в обобщенном уравнении типа (2.203) становится равным или близок к нулю. 2.14. МОДИФИЦИРОВАННЫЕ И ПРОИЗВОДНЫЕ |
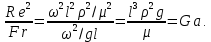 | (2.213) |
Полученный производный критерий носит название критерий Галилея. Умножая этот критерий на относительную разность плотностей жидкости в различных точках
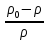 , являющуюся причиной движения, находят новый производный критерий – критерий Архимеда:
, являющуюся причиной движения, находят новый производный критерий – критерий Архимеда: 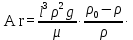 | (2.214) |
Если заменить симплекс
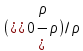 на пропорциональную ему относительную разность температур, более удобную для измерений, то получается новый производный критерий, являющийся критерием теплового подобия Грасгофа (Gr).
на пропорциональную ему относительную разность температур, более удобную для измерений, то получается новый производный критерий, являющийся критерием теплового подобия Грасгофа (Gr).где F — поверхность спокойной жидкости в аппарате; p — давление воздуха, 1 бар; k — коэффициент.
При слабом перемешивании k
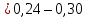 , для малоинтенсивного 0,35–0,50, а для интенсивного 0,45–0,60.
, для малоинтенсивного 0,35–0,50, а для интенсивного 0,45–0,60.При расчете барботеров расход воздуха на 1 м2 свободной поверхности можно принять 0,4; 0,8 и 1,0 м3/мин для слабого, среднего и интенсивного перемешивания.
Перемешивание в трубопроводах осуществляют путем повышения турбулентности потока жидкости при достаточной длинеl и диаметре трубыd. Иногда применяют специальные вставки или винтовые насадки.
Сопла в аппаратах применяют для перемешивания циркуляционным способом. Поступление в сопло жидкости происходит за счет разности давлений между его входом и выходом. Для более интенсивного перемешивания при подаче жидкости в сопло циркуляционным насосом. Оптимальным размером сопла для перемешивания является отношение от устья сопла x к его диаметру d равное
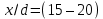 .
.БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Касаткин, А. Г. Основные процессы и аппараты химической технологии: учеб. для вузов / А. Г. Касаткин. – 11-е изд. стереотип. и дораб. – М. : Альянс, 2005. – 753 с.
Павлов, К. Ф. Примеры и задачи по курсу процессов и аппаратов химической технологии: учеб. пособие для вузов / К. Ф. Павлов, П. Г. Романков, А. А. Носков. – М. : Альянс, 2013. – 576 с.
Плаксин, Ю. М. Процессы и аппараты пищевых производств: учеб. для вузов / Ю. М. Плаксин, Н. Н. Малахов, В. А. Ларин. – 2-е изд. перераб. и доп. – М. : КолосС, 2007. – 760 с.
Процессы и аппараты пищевых производств: учеб. для вузов. В 2 кн. Кн. 1 / А. Н. Остриков [и др.] ; под общ. ред. А. Н. Острикова. – СПб: ГИОРД, 2007. – 704 с..
Кавецкий, Г. Д., Васильев, Б. В. Процессы и аппараты пищевой технологии: учеб. пособие / Г. Д. Кавецкий, Б. В. Васильев. – 2-е изд. перераб. и доп. – М. : Колос, 2000. – 551 с.
Малахов, Н. Н. Процессы и аппараты пищевых производств: учеб. для вузов / Н. Н. Малахов, Ю. М. Плаксин, В. А. Ларин. – Орел : Изд-во ОГТУ, 2001. – 687 с.
Дытнерский, Ю. И. Основные процессы и аппараты химической технологии: учеб. пособие по проектированию / Ю. И. Дытнерский. – М. : Химия, 1983. – 272 с.
Таранцева, К. Р. Процессы и аппараты химической технологии в технике защиты окружающей среды: учеб. пособие / К. Р. Таранцева, К. В. Таранцев. – М. : ИНФА-М, 2016. – 412 с.
Плохов, С.В. Организация теплообмена в биотехнологических производствах: учеб. пособие / С.В. Плохов, И.Г. Трунова. – Нижний Новгород: НГТУ, 2018. – 80с.

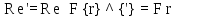
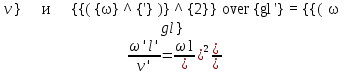
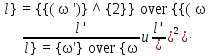
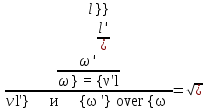
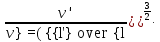
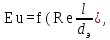
 в критерий
в критерий 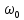 . Получаемые при этом видоизмененные критерии называют модифицированными.
. Получаемые при этом видоизмененные критерии называют модифицированными.