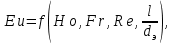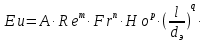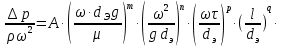ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
2.12. ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕРанее отмечалось, что дифференциальные уравнения Навье - Стокса невозможно решить для большинства практически важных случаев. Однако теория подобия позволяет представить их решения в виде общей функциональной зависимости между критериями подобия, характеризующими силы, действующие при движении вязкой жидкости. Воспользуемся развернутой формулой уравнения Навье - Стокса вдоль вертикальной оси OZ: 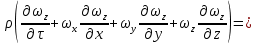 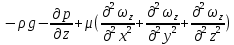 . (2.192) . (2.192)Получим критерии, используя первую теорему подобия, то есть путем деления левой части равенства на правую (или наоборот) и последующего отбрасывания знаков математических операторов. Если движение жидкости установившееся, то 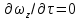 и выражение в левой части равенства (2.190) является силой инерции и выражение в левой части равенства (2.190) является силой инерции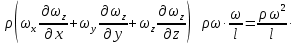 (2.193) (2.193)В правой части выражения (2.190) произведение 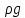 характеризует силу тяжести, а слагаемое характеризует силу тяжести, а слагаемое 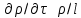 отражает действие силы давления. Наконец, последнее слагаемое правой части является силой трения отражает действие силы давления. Наконец, последнее слагаемое правой части является силой трения
Разделим члены первой части выражения (2.192) на левую часть, то есть на силу инерции. Получим соотношения между соответствующими силами, иначе говоря, выразим эти силы в относительных единицах, приняв за масштаб силу инерции. Получим безразмерные комплексы, являющиеся критериями подобия. Отношение силы тяжести к силе инерции
называется критерием Фруда и обозначается 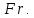 Этот критерий отражает влияние силы тяжести или собственного веса на движение жидкости. Этот критерий отражает влияние силы тяжести или собственного веса на движение жидкости.Соотношение (2.195), чтобы избежать чисел меньше единицы, обычно представляют в виде обратного выражения:
Отношение силы давления к силе инерции называют критерием Эйлера
В критерии Эйлера обычно вместо абсолютного давления используют разность давлений 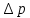 между какими-либо двумя точками жидкости: между какими-либо двумя точками жидкости:
Этот критерий отражает влияние изменения (перепада) гидростатического давления на движение жидкости. Отношение силы трения к силе инерции обычно представляют в виде обратного выражения, которое называется критерием Рейнольдса
Критерий Рейнольдса отражает влияние силы трения на движение жидкости. Величина 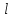 в этом критерии, как и в других критериях подобия, представляет собой определяющий линейный размер. При движении жидкости по трубопроводам и аппаратам круглого сечения за такой размер принимается их диаметр, а для некруглого сечения - эквивалентный диаметр в этом критерии, как и в других критериях подобия, представляет собой определяющий линейный размер. При движении жидкости по трубопроводам и аппаратам круглого сечения за такой размер принимается их диаметр, а для некруглого сечения - эквивалентный диаметр 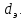 При неустановившемся движении жидкости При неустановившемся движении жидкости 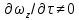 и в уравнении Навье-Стокса появляется еще один член и в уравнении Навье-Стокса появляется еще один член
отражающий влияние не стационарности движения. Отношение силы инерции к этому слагаемому называется критерием гомохронности, который обозначается Но. Этот критерий учитывает неустановившийся характер движения в подобных потоках
Во всех сходственных точках движущихся подобно жидкостей  (2.202) (2.202)Согласно второй теореме подобия, решение уравнения Навье-Стокса должно представлять функциональную зависимость между введёнными критериями. В ряде случаев эту зависимость дополняют симплексами геометрического подобия. При движении жидкости через трубы или каналы такими симплексами являются отношение длины 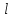 трубы и её эквивалентного диаметра. Тогда критериальное уравнение, являющееся решением уравнений Навье-Стокса, принимает окончательный вид трубы и её эквивалентного диаметра. Тогда критериальное уравнение, являющееся решением уравнений Навье-Стокса, принимает окончательный вид
Все входящие в это уравнение критерии, кроме критерия Эйлера являются определяющими. Критерий 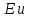 содержит величину содержит величину 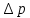 , не входящую в условия однозначности. Поэтому выражение (2.203) представляют в виде обобщенного или критериального уравнения гидродинамики , не входящую в условия однозначности. Поэтому выражение (2.203) представляют в виде обобщенного или критериального уравнения гидродинамики
которое чаще все аппроксимируют степенной зависимостью, то есть придают вид
После подстановки в это выражение значений критериев получим
Коэффициент 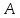 и показатели степеней находят опытным путем, представляя данные в логарифмических координатах. Если движение жидкости стационарное, то критерий и показатели степеней находят опытным путем, представляя данные в логарифмических координатах. Если движение жидкости стационарное, то критерий 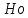 можно исключить из выражения (2.206). Когда еще и сила тяжести не играет существенной роли, то критерий можно исключить из выражения (2.206). Когда еще и сила тяжести не играет существенной роли, то критерий 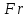 также можно не учитывать. В этом случае выражение (2.206) переходит в приводившееся ранее уравнение (2.191) при условии также можно не учитывать. В этом случае выражение (2.206) переходит в приводившееся ранее уравнение (2.191) при условии 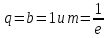 . Из уравнения (2.206) обычно находят . Из уравнения (2.206) обычно находят 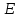 u, а по нему u, а по нему 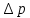 . При движении жидкости по трубопроводу или через аппарат величина . При движении жидкости по трубопроводу или через аппарат величина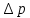 является потерей давления и в конечном счёте характеризует энергию необходимую для перемещения жидкости с заданной скоростью и расходом. является потерей давления и в конечном счёте характеризует энергию необходимую для перемещения жидкости с заданной скоростью и расходом. |

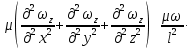
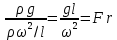
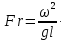
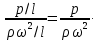
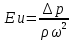

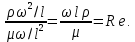
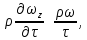
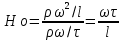
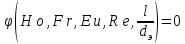 .
.