ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
2.9 ПРАКТИЧЕСКОЕ ПРИЛОЖЕНИЕ |
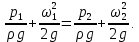 | (2.149) |
Откуда разность давлений h, измеряемая U–образной трубкой равна
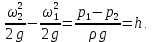 | (2.150) |
Чтобы определить среднюю скорость потока и объемный расход, воспользуемся уравнением сплошности потока и выразим
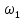 :
: 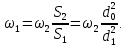 | (2.151) |
Подставим это выражение в (2.150) и выразим скорость сжатой струи
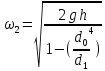 | (2.152) |
Зная величину
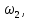 по формуле (2.151) можно найти значение
по формуле (2.151) можно найти значение 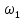 , а затем и расход, учитывая, что
, а затем и расход, учитывая, что 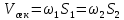 .Таким образом рассчитывают расход для сопел и труб Вентури. Для диафрагм
.Таким образом рассчитывают расход для сопел и труб Вентури. Для диафрагм 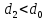 , поэтому
, поэтому 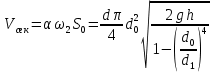 , , | (2.153) |
где α – поправочный коэффициент меньше единицы, учитывающий, что скорость сжатой струи больше скорости в отверстии, поскольку
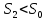 .
.Коэффициент α называется коэффициентом расхода дроссельного прибора. Он зависит от режима движения жидкости и от соотношения диаметров отверстия и трубопровода, т. е.
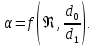
Поскольку величина
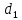 больше диаметра отверстия в 3-4 раза, то их отношением в последнем выражении можно пренебречь. Следовательно
больше диаметра отверстия в 3-4 раза, то их отношением в последнем выражении можно пренебречь. Следовательно 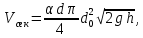 | (2.154) |
а среднюю скорость вычислить через расход упустив индекс «1»
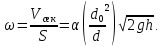 | (2.155) |
При работе с упругими жидкостями используют два последних выражения, вводя еще один поправочный коэффициент, учитывающий изменение плотности при сжатии. Его значения, также как и значение
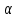 , табулированы. Кроме того, с помощью уравнения Бернулли можно рассчитывать процессы истечения жидкостей из резервуаров через отверстия в тонком днище, тонкой боковой стенке или через насадки. Рассчитать процесс истечения – это определить скорость и время опорожнения резервуара. Отверстие в тонком днище или в тонкой стенке означает, что толщина днища или стенки более чем в 2 раза меньше диаметра отверстия. Насадками называют короткие патрубки (куски трубы) различной формы, присоединенные к отверстию в тонкой стенке. Длина насадок составляет примерно 3-4 диаметра трубы. Насадки бывают (рис. 2.16) внешними и внутренними, коническими расходящимися и коническими сходящимися, а также коноидальными.
, табулированы. Кроме того, с помощью уравнения Бернулли можно рассчитывать процессы истечения жидкостей из резервуаров через отверстия в тонком днище, тонкой боковой стенке или через насадки. Рассчитать процесс истечения – это определить скорость и время опорожнения резервуара. Отверстие в тонком днище или в тонкой стенке означает, что толщина днища или стенки более чем в 2 раза меньше диаметра отверстия. Насадками называют короткие патрубки (куски трубы) различной формы, присоединенные к отверстию в тонкой стенке. Длина насадок составляет примерно 3-4 диаметра трубы. Насадки бывают (рис. 2.16) внешними и внутренними, коническими расходящимися и коническими сходящимися, а также коноидальными. 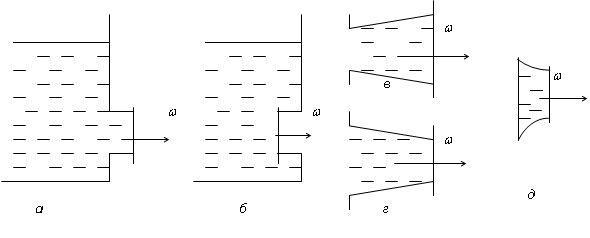 |
| Рис. 2.16. Виды насадок: а – внешние; б – внутренние; в - конические расходящиеся; г - конические сходящиеся; д - коноидальные |
Истечение жидкости может происходить в атмосферу или в слой жидкости при постоянном или переменном напоре. Рассмотрим истечение жидкости в тонком днище открытого сосуда, в котором поддерживается постоянный уровень H жидкости (рис. 2.17). Выбрав плоскость сравнения параллельно днищу сосуда, напишем уравнение Бернулли для сечений
1-1, соответствующего верхнему уровню жидкости в сосуде, и для сечения 2-2, плоскость которого проходит через самое узкое сечение вытекающей струи
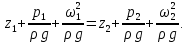 | (2.156) |
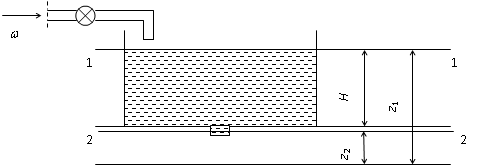 |
| Рис. 2.17. К истечению жидкости через отверстие в тонком дне |
Для открытого сосуда
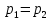 . Кроме того, при постоянно уровне жидкости
. Кроме того, при постоянно уровне жидкости 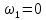 . Пренебрегая небольшим расстоянием от плоскости 2-2 до днища сосуда, можно принять, что
. Пренебрегая небольшим расстоянием от плоскости 2-2 до днища сосуда, можно принять, что 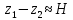 . С учетом этих условий
. С учетом этих условий 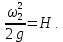 | (2.157) |
Следовательно
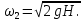 | (2.158) |
При движении реальной жидкости часть напора H теряется на трение и на преодоление сопротивления, вызванного внезапным сужением потока в отверстии. Поэтому скорость реальной жидкости должна быть
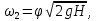 | (2.159) |
где
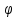 - это поправочный коэффициент (
- это поправочный коэффициент (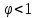 ), учитывающий потери напора при истечении через отверстие, называемый коэффициентом скорости.
), учитывающий потери напора при истечении через отверстие, называемый коэффициентом скорости.В целом площадь поперечного сечения струи в отверстии
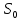 больше площади ее самого узкого сечения
больше площади ее самого узкого сечения 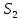 , поэтому скорость жидкости в отверстии
, поэтому скорость жидкости в отверстии 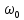 должна быть меньше чем
должна быть меньше чем 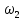 .
. 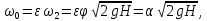 | (2.160) |
где
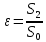 – коэффициент сжатия струи;
– коэффициент сжатия струи; 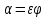 - коэффициент расхода.
- коэффициент расхода.Сжатие струи в отверстии приводит к тому, что ее диаметр составляет около 80% от внутреннего диаметра отверстия. Уравнение (2.160) справедливо так же и для расчета скорости истечения жидкости через отверстие в тонкой боковой стенке, если считать H расстоянием от верхнего уровня жидкости до оси отверстия.
Объемный расход жидкости равен произведению ее скорости в отверстии на площадь сечения отверстия
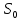 .
.  | (2.161) |
Из этого уравнения следует, что расход жидкости, вытекающей через отверстие в тонком днище (или стенке), зависит от высоты постоянного уровня жидкости над отверстием и от размера отверстия, но не зависит от формы сосуда.
Коэффициент
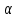 определяют опытным путем. Его значение зависит от режима течения и свойств жидкости. В справочной литературе для различных жидкостей есть зависимости
определяют опытным путем. Его значение зависит от режима течения и свойств жидкости. В справочной литературе для различных жидкостей есть зависимости 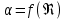 . Однако для жидкостей по вязкости не очень отличающихся от воды в первом приближении для отверстий можно принимать
. Однако для жидкостей по вязкости не очень отличающихся от воды в первом приближении для отверстий можно принимать 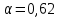 а для насадок
а для насадок 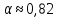 .
.Когда истечение жидкости происходит через отверстие в тонком днище при переменном уровне жидкости, скорость истечения
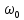 снижается с уменьшением H, т. е. процесс имеет нестационарный характер.
снижается с уменьшением H, т. е. процесс имеет нестационарный характер.За бесконечно малое время
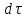 через отверстие или насадок вытечет объем жидкости
через отверстие или насадок вытечет объем жидкости 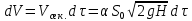 | (2.162) |
За это же время уровень жидкости в сосуде постоянного сечения S понижается на величину dH, то есть вытекаемый объем составит
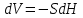 | (2.163) |
Тогда согласно уравнению неразрывности потока
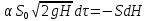 | (2.164) |
откуда
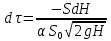 | (2.165) |
Время опорожнения ёмкости при постоянном уровне жидкости лишено физического смысла. Однако можно рассчитать время
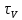 , за которое из емкости вытечет первоначальный объем жидкости
, за которое из емкости вытечет первоначальный объем жидкости 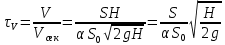 | (2.166) |
В уравнении (2.165) разделены переменные. Принимая неизменность площади поперечного сечения резервуара с высотой, можно проинтегрировать выражение (2.165) на интервалах
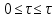 и
и 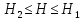 . В результате интегрирования получим:
. В результате интегрирования получим: 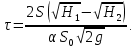 | (2.167) |
В случае полного опорожнения резервуара
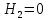 ,
, 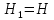 , и время опорожнения найдется по формуле
, и время опорожнения найдется по формуле 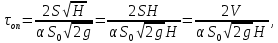 | (2.168) |
где V- объем жидкости в резервуаре.
Сравнивая (2.166) и (2.168) можно сделать вывод, что время опорожнения емкости при снижающемся напоре в два раза больше, чем
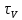 . Таким образом, при постоянном напоре скорость движения жидкости в два раза выше, чем при снижающемся напоре. Выражение (2.167) справедливо лишь в случаях, когда поперечное сечение ёмкости не изменяется с высотой, т. е. при интегрировании (2.165) принимается, что
. Таким образом, при постоянном напоре скорость движения жидкости в два раза выше, чем при снижающемся напоре. Выражение (2.167) справедливо лишь в случаях, когда поперечное сечение ёмкости не изменяется с высотой, т. е. при интегрировании (2.165) принимается, что 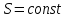 .
.Если емкость имеет цилиндрическую форму, но расположена горизонтально (танк), то
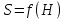 и время опорожнения рассчитывают по формуле
и время опорожнения рассчитывают по формуле 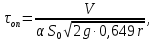 | (2.169) |
где
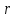 - радиус резервуара.
- радиус резервуара.Выражение (2.169) справедливо при степени заполнения емкости равной 0,8.

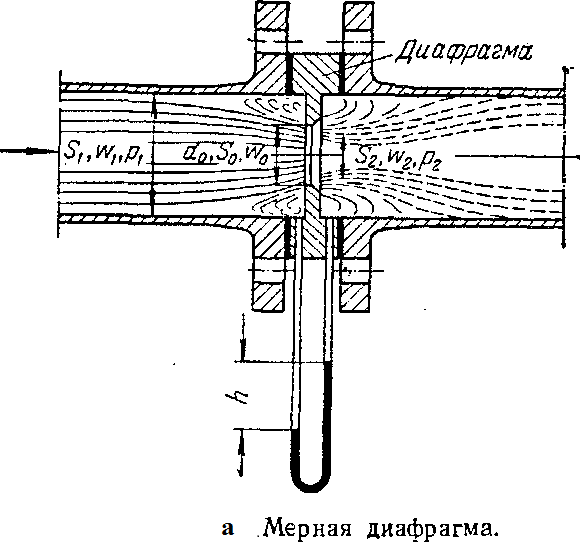
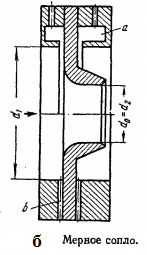
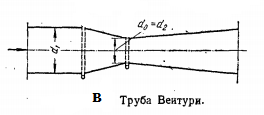
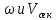 применяют U-образные трубки (рис. 2.5), а также дроссельные приборы, включающие мерные диафрагмы, сопла и трубы Вентури
применяют U-образные трубки (рис. 2.5), а также дроссельные приборы, включающие мерные диафрагмы, сопла и трубы Вентури 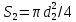 равна площади самого отверстия
равна площади самого отверстия 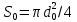 . Площадь сечения потока жидкости в трубопроводе составляет
. Площадь сечения потока жидкости в трубопроводе составляет 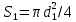 .
.