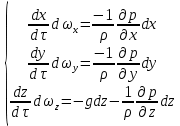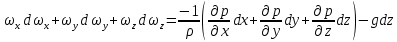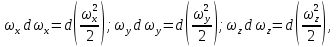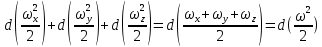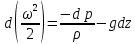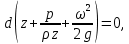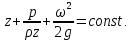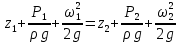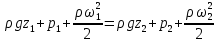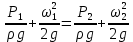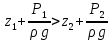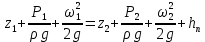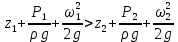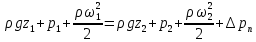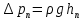ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
2.8. УРАВНЕНИЕ БЕРНУЛЛИДля решения уравнений движения Эйлера в случае установившегося потока жидкости (2.118) умножим каждое из них на 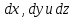 , соответственно, и разделим на плотность жидкости , соответственно, и разделим на плотность жидкости 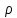 . В результате получим . В результате получим
Сложим эти уравнения, учитывая, что производные 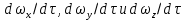 равны проекциям скорости на соответствующие оси равны проекциям скорости на соответствующие оси 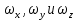 , тогда: , тогда:
Слагаемые левой части представим следующим образом:
а значит их сумма
где 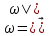 - модуль вектора скорости. - модуль вектора скорости. В правой части выражения (2.134) сумма слагаемых в скобках является полным дифференциалом 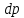 , поскольку при установившемся режиме давление в каждой точке не зависит от времени, а меняется лишь с координатами. Следовательно , поскольку при установившемся режиме давление в каждой точке не зависит от времени, а меняется лишь с координатами. Следовательно
Разделим обе части этого выражения на величину 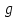 и представим сумму дифференциалов как в дифференциал суммы и представим сумму дифференциалов как в дифференциал суммы
откуда получается уравнение Бернулли для установившегося движения идеальной жидкости
Два первых слагаемых из левой части этого выражения входили в основное уравнение гидростатики. Они являются нивелирной высотой и статическим напором, а в сумме представляют удельную потенциальную энергию. Величина 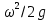 называется скоростным или динамическим напором. Из размерности называется скоростным или динамическим напором. Из размерности
следует, что она является удельной кинетической энергией движения жидкости. Таким образом, из уравнения Бернулли следует, что при установившемся движении идеальной жидкости сумма удельной потенциальной и кинетической энергии жидкости для каждого поперечного сечения потока остаётся постоянной для каждого поперечного сечения потока. Иногда сумму слагаемых в левой части выражения (2.139) называют гидродинамическим напором. Следовательно, для всех поперечных сечений установившегося потока идеальной жидкости величина гидродинамического напора остаётся постоянной. Для любых двух поперечных сечений 1 и 2 по направлению движения жидкости уравнение Бернулли запишется
Если умножить обе части выражения на удельный вес жидкости 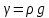 , то уравнение примет вид , то уравнение примет вид
где каждое слагаемое представляет удельную энергию, отнесённую к единице объема 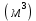 , а не веса. , а не веса.При горизонтальном расположении трубопровода 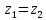 и уравнение Бернулли (2.141) выразится формулой и уравнение Бернулли (2.141) выразится формулой
Если при постоянном расходе жидкости площадь сечения 2-2 меньше, чем сечение 1-1, то 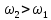 и удельная кинетическая энергия и удельная кинетическая энергия 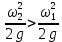 . .Согласно уравнению Бернулли (2.141) для сохранения постоянства гидродинамического напора
Это означает, что при сужении трубопровода часть потенциальной энергии давления 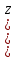 не меняются) переходит в кинетическую энергию. Таким образом, уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока. не меняются) переходит в кинетическую энергию. Таким образом, уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока. Уравнение Бернулли при движении реальной жидкости через два любых сечения 1-1 и 2-2, расположенных походу движения жидкости имеет вид
где 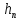 – потерянный напор, характеризующий удельную (то есть отнесённую к единице веса жидкости) теряемую энергию. – потерянный напор, характеризующий удельную (то есть отнесённую к единице веса жидкости) теряемую энергию. Значит, для движения реальной жидкости существует неравенство
Это связано с тем, что при движении реальных жидкостей действуют силы внутреннего трения, обусловленные вязкостью жидкости и режимом ее движения, а также силы трения о стенки трубы. Эти силы оказывают сопротивление движению жидкости, которое называется гидродинамическим сопротивлением. На его преодоление должно расходоваться некоторая часть энергии потока. Поэтому общее количество энергии по длине потока будет непрерывно уменьшаться вследствие перехода потенциальной энергии в потерянную энергию, затрачиваемую на трение и безвозвратно теряемую при рассеивании тепла в окружающую среду. Таким образом, величина 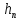 в уравнении (2.145) характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости. в уравнении (2.145) характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.Уравнение (2.145) может быть представлено в другом виде, если обе части умножить на 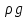 : :
В этом уравнении величина 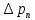 является потерянным давлением, равным является потерянным давлением, равным
Определение потерь напора или давления составляет практически важную задачу, связанную с расходом энергии, необходимой для перемещения реальных жидкостей насосами, компрессорами и так далее. Трудность решения этой задачи вызвана невозможностью в большинстве случаев получать аналитические решения дифференциальных уравнений Навье – Стокса. |