ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"

• Название: Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
• Дата: 30.03.2022
• Размер: 1.06 Mb.
• Имя файла: ЛекцПРиА.docx
• Тип: Конспект; #429098
• страница: 7 из 14

2.6 ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЙЛЕРА
ДЛЯ ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ

Дифференциальные уравнения движения отражают связь между давлением и скоростью движения жидкости. Как и при выводе дифференциальных уравнений равновесия (рис.2.2), выделим в потоке движущейся жидкости элементарный объем . Ранее указывалось, что проекции на оси координат сил тяжести и давления, действующих на параллелепипед, составляют:

для оси ОХ		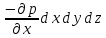(2.113)
для оси ОУ		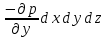(2.114)
а для оси ОZ		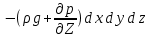(2.115)

Согласно основному принципу динамики (второму закону Ньютона), сумма проекций сил действующих на элементарный объем движущейся жидкости должна равняться произведению массы жидкости на её ускорение. Масса жидкости в объеме параллелепипеда

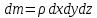(2.116)

Если скорость жидкости 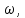то её ускорение составит 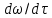, а его проекции на отдельные оси выражаются субстанциональными производным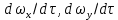и и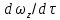 . Тогда в соответствии с основным принципом динамики

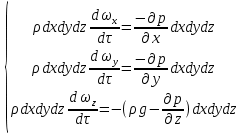(2.117)

или после сокращения

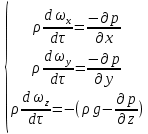(2.118)

Когда поток жидкости является установившимся, изменение составляющих скоростей в фиксированных точках пространства не зависят от времени, то есть производные 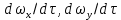и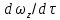 равны нулю. В этом случае изменение скорости зависит только от координат. Следовательно, ускорения вдоль отдельных осей

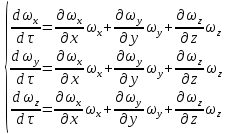(2.119)

Система уравнений (2.118) в сочетании с системой (2.119) являются дифференциальными уравнениями движения идеальной жидкости Эйлера для установившегося потока.

Для неустановившегося потока, изменение составляющих скорости проходит также во времени в фиксированных точках пространства. Производные 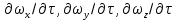не равны нулю и ускорения вдоль отдельных осей имеет вид:

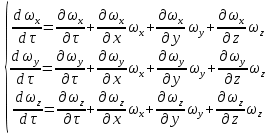(2.120)

Система уравнений (2.118) в сочетание с системой (2.120) являются дифференциальными уравнениями движения идеальной жидкости Эйлера для неустановившегося потока. Интегрирование системы (2.118) для установившегося потока приводит к уравнению Бернулли, широко применяемому для решения многих технических задач.
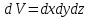