ЛекцПРиА. Конспект лекций по дисциплине "Процессы и аппараты биотехнологии"
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
2.3 ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ |
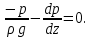 | (2.30) |
Умножая обе части этого уравнения на
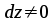 и деля на
и деля на 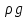 имеем:
имеем: 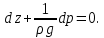 | (2.31) |
Для несжимаемой жидкости плотность постоянна, следовательно
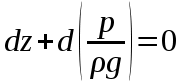 | (2.32) |
или, используя свойство дифференциала:
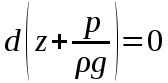 | (2.33) |
откуда, после интегрирования:
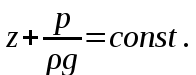 | (2.34) |
Выражение (2.34) называется основным уравнением гидростатики или законом Паскаля. Его физический смысл вытекает из анализа размерностей слагаемых:
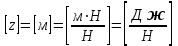 | (2.35) |
и
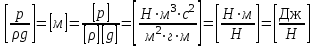 | (2.36) |
Видно, что оба слагаемых являются удельной энергией, то есть энергией, приходящейся на единицу веса жидкости. Величина z является удельной потенциальной энергией положения, так как связана с координатой. Величина
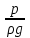
 характеризует удельную потенциальную энергию давления в данной точке. Сумма этих величин является общей удельной потенциальной энергией. Таким образом, выражение (2.34) является частным случаем закона сохранения энергии, а физический смысл закона Паскаля отражается в следующей формулировке:
характеризует удельную потенциальную энергию давления в данной точке. Сумма этих величин является общей удельной потенциальной энергией. Таким образом, выражение (2.34) является частным случаем закона сохранения энергии, а физический смысл закона Паскаля отражается в следующей формулировке: Удельная потенциальная энергия во всех точках покоящейся жидкости есть величина постоянная.
Физический смысл основного уравнения гидростатики становится понятен из рассмотрения рис. 2.3, на котором изображен сосуд с однородной капельной жидкостью.
Применительно к точке 2, находящейся на поверхности жидкости, и к произвольной точке 1 рисунка 2.3 закон Паскаля запишется
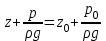 | (2.37) |
или
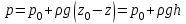 | (2.38) |
где p0 и p – давление в точке 2 и в произвольной точке 1, соответственно; z0 и z– высота точки 2 и произвольной точки 1 относительно выбранной плоскости отсчета 0 – 0; - плотность жидкости; g – ускорение свободного падения; h – разность высот z0 и z.
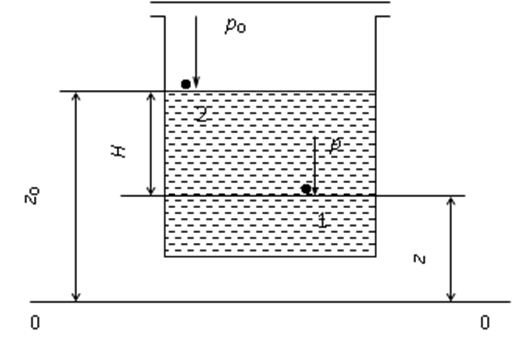 |
| Риc. 2.3. К пояснению физического смысла основного уравнения гидростатики |
Величину p/g называют статическим напором (м). Величины z и z0 называются нивелирными высотами (м).
Основное уравнение гидростатики имеет ряд практических приложений.
1. Принцип сообщающихся сосудов и его использование
Пусть два открытых сообщающихся сосуда заполнены одной жидкостью (рис. 2.4, а) с плотностью . Выберем плоскостью отсчета (0 – 0) плоскость, на которой находятся точки A и A.
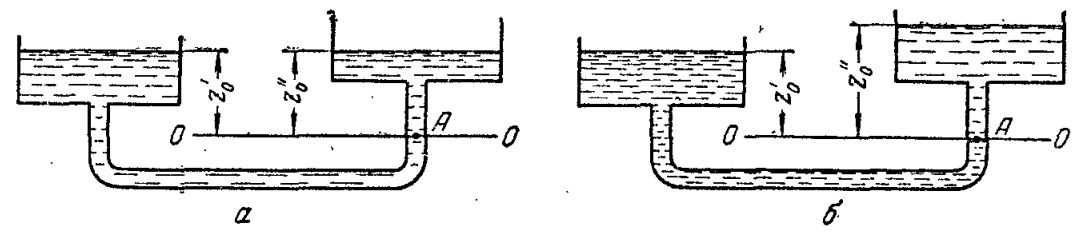 |
| Рис. 2.4. Условия равновесия в сообщающихся сосудах для одной жидкости (а) и для разнородных несмешивающихся жидкостей (б) |
Для точки A основное уравнение гидростатики согласно выражению (2.38) запишется
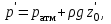 | (2.39) |
а для точки A
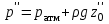 | (2.40) |
Величины z и z равны нулю, поскольку точки A и A лежат на плоскости отсчета.
При равновесии в каждой точке давление одинаково во всех направлениях, поскольку в противном случае происходило бы перемещение жидкости. Следовательно, давления в точках A и A, определяемые из уравнений (2.39) и (2.40), должны быть равны, а значит
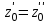 .
.Таким образом, в закрытых и открытых сообщающихся сосудах, находящихся под одинаковым давлением, заполненных однородной жидкостью, уровни жидкости с одинаковым давлением расположены на одной высоте независимо от формы и поперечного сечения сосудов. Этот принцип используется для измерения уровня жидкости в закрытых аппаратах с помощью водомерных стекол.
Если сосуды заполнены двумя несмешивающимися жидкостями (рис. 2.4, б), имеющими плотности (в левом сосуде) и (в правом сосуде), то, проводя плоскость сравнения 0 – 0 через границу раздела жидкостей, получим
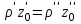 | (2.41) |
или
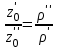 | (2.42) |
Таким образом, в сообщающихся сосудах высоты уровней разнородных жидкостей над поверхностью их раздела обратно пропорциональны плотностям этих жидкостей. Это свойство также используется в устройствах для измерения уровней жидкости в закрытых сосудах, когда есть ограничения по высоте измерительного столба.
Если сосуды заполнены одной жидкостью с плотностью , но давления жидкости в них не одинаковы и равны p (в левом сосуде) и p (в правом сосуде), то
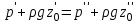 | (2.43) |
то есть разность уровней жидкости в сосудах
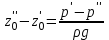 | (2.44) |
Уравнение (2.44) применяют при измерениях разности давлений между различными точками с помощью дифференциальных U-образных манометров (рис. 2.5).
На входе и выходе манометра разные давления, что связано с движением жидкости, причем:
 | (2.45) |
где - средняя скорость движения жидкости в трубопроводе, м/с.
 |
| Рис. 2.5. Принцип работы дифференциального манометра |
2. Определение высоты гидравлического затвора
Условия равновесия жидкости позволяют определить высоту гидравлического затвора различных аппаратов. Например, высота гидравлического затвора молочного сепаратора непрерывного действия определяет высоту расположения патрубка для отвода сливок.
Смесь жидкостей различной плотности поступает в аппарат 1 (рис. 2.6) по центральной трубе 2 и расслаивается в нем. Причем более легкая жидкость с плотностью удаляется сверху через штуцер 3, а более тяжелая жидкость с плотностью отводится снизу через U-образный затвор 4.
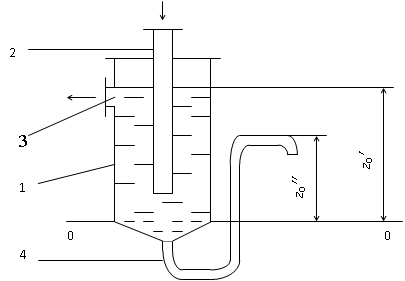 |
| Рис. 2.6. К определению высоты гидравлического затвора сепаратора: 1 – сепаратор; 2 – труба; 3 – штуцер; 4 - затвор |
Уровень раздела жидкостей поддерживается на границе цилиндрической и конической частей аппарата. Если плоскость сравнения провести через эту границу, то высота гидравлического затвора при равенстве давлений внутри аппарата и на выходе из затвора согласно уравнению (2.41) составит
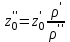 . . | (2.46) |
3. Пневматическое измерение объема и массы жидкости в резервуарах
Часто приходится измерять объем и массу жидкости в подземных резервуарах (рис. 2.7). Для этого в емкость 1 помещают трубу 2 так, чтобы ее нижний конец доходил почти до самого дна.
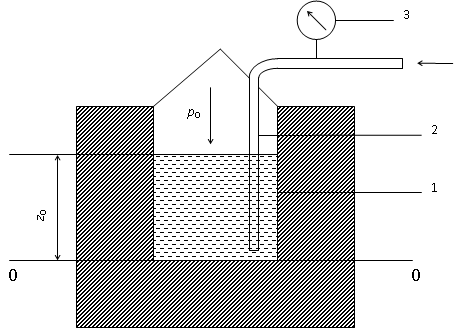 |
| Рис. 2.7. Пневматический измеритель уровня жидкости: 1 – емкость; 2 – труба; 3 - манометр |
Давление над жидкостью составляет p0. По трубе 2 подают сжатый газ (обычно воздух), постепенно повышая его давление, которое замеряется манометром 3. Когда газ преодолевает давление столба жидкости в трубе, он барботирует через жидкость при постоянном давлении
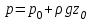 , , | (2.47) |
откуда уровень жидкости в резервуаре:
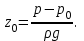 | (2.48) |
Зная высоту столба жидкости и площадь поперечного сечения резервуара Sp, можно определить объем жидкости Vж и по известной плотности ее массу
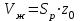 | (2.49) |
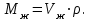 | (2.50) |
4. Расчет гидравлических прессов
Гидравлические прессы широко применяются в биотехнологических, особенно в пищевых, производствах для прессования, брикетирования и формования различных материалов (рис. 2.8).
 |
| Рис. 2.8. Принципиальная схема гидравлического пресса: 1, 2 – поршни; 3 – материал; 4 - плита |
Если приложить небольшое усилие P1 под действием давления р к поршню 1, движущемуся в цилиндре меньшего диаметра d1, то такое же давление будет приложено к поршню 2 с диаметром d2. Сила давления на поршень 1 составит
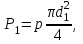 | (2.51) |
а на поршень 2 сила давления составит:
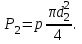 | (2.52) |
Разделив последнее выражение на уравнение (2.51), получим:
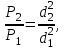 | (2.53) |
т. е. выигрыш в силе будет прямо пропорционален отношению квадратов диаметров поршней или отношению площадей поршней. Таким образом, с помощью небольших усилий проводят прессование материала 3 между поршнем 2 и неподвижной плитой 4.
5. Определение давления жидкости на дно и стенки аппарата
или емкости
В плоскости на уровне дна аппарата гидростатическое давление во всех точках одинаково
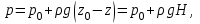 | (2.54) |
где H – высота жидкости в емкости или аппарате.
Следовательно, сила давления Р на горизонтальное дно не зависит от формы аппарата и объема жидкости в нем, а определяется лишь высотой столба жидкости и площадью F дна сосуда
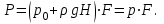 | (2.55) |
Гидростатическое давление на вертикальную стенку аппарата изменяется по высоте. Следовательно, сила давления на стенку тоже изменяется по высоте аппарата, поэтому
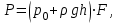 | (2.56) |
где h – расстояние от верхнего уровня жидкости до центра тяжести смоченной площади F стенки.
Достаточно часто h = 0,5H. Зная максимальную силу Pmax, действующую на дно или стенку аппарата, можно определить минимальную толщину стенки при условии, что Pmax<Pраз или
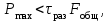 | (2.57) |
где Pmax – сила разрыва стенки аппарата; раз – напряжение разрыва, Н/м2; Fобщ – площадь внутренней поверхности аппарата.
Напряжение разрыва зависит от природы применяемого конструкционного материала и его толщины. Эти зависимости приведены в справочной литературе по конструкционным материалам. При вычислении Pmax следует учитывать, что на стенку с внешней стороны аппарата действует давление р0. Поэтому, исходя из выражения (2.56), максимальная сила, действующая на дно или стенку аппарата, будет являться наибольшим значением после расчетов по формуле
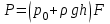 | (2.58) |

 . Следовательно, указанную систему уравнений можно свести к одному линейному, заменив частную производную
. Следовательно, указанную систему уравнений можно свести к одному линейному, заменив частную производную 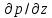 на обычную для функции одного аргумента
на обычную для функции одного аргумента 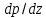 , тогда получаем:
, тогда получаем: