6. Л Б1.В.ОД14 ТЭАХД (полный текст). Конспект лекций по направлению подготовки 38. 03. 01 Экономика профиль Экономика предприятий и организаций (транспорт)
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
ТЕМА 2 КЛАССИФИКАЦИЯ ПРИЕМОВ И СПОСОБОВ ЭКОНОМИЧЕСКОГО АНАЛИЗАВ качестве важнейшего элемента методики технико-экономического анализа выступают технические приемы и способы анализа. Применение тех или иных способов зависит от цели и глубины анализа, объекта исследования, технических возможностей выполнения расчетов и т. д. Кратко их можно назвать инструментарием анализа, который используется на разных этапах исследования: – с целью первичной обработки собранной информации (проверки, группировки, систематизации); – изучения состояния и закономерностей развития исследуемых объектов; – определения влияния тех или иных факторов на результаты деятельности предприятий; – оценки неиспользованных и перспективных резервов для повышения эффективности производства; – обобщения результатов и комплексной оценки деятельности предприятий; – обоснования планов экономического и социального развития, управленческих решений, различных мероприятий. Среди известных способов экономического анализа хозяйственной деятельности предприятий можно выделить: – традиционные (сравнение, относительных и средних величин, графический, аналитических группировок, балансовый) – для обработки и изучения информации; – детерминированного факторного анализа (индексный способ, способ цепных подстановок, способ абсолютных разниц, способ относительных разниц, способ корректировок, способ относительных коэффициентов, способ пропорционального деления и долевого участия, способ структурных сдвигов, кольцевой способ, логарифмический способ и др.); – стохастические (корреляционный, дисперсионный, компонентный и др.); – оптимизации показателей (экономико-математический, программирование, теория массового обслуживания и др.) – для изучения влияния факторов на результаты хозяйственной деятельности. 1 Традиционные способы анализа Сравнение величин одноименных показателей – это наиболее распространенный способ анализа. Он применяется для количественной и качественной оценки изменения уровня исследуемых показателей. Результаты сравнения выражаются в абсолютных или относительных величинах, показывающих, на сколько единиц, во сколько раз или на сколько процентов изучаемое явление больше или меньше взятого за базу сравнения. В качестве базы для сравнения могут быть приняты: плановое задание, отчетные данные предшествующих периодов, среднеотраслевые величины показателей, данные однотипных предприятий и т. п. Выбор базы для сравнения определяется целью экономического исследования. Применяя способ сравнения величин, важно обеспечить сопоставимость сравниваемых показателей, поскольку сравнивать можно только качественно однородные величины. При этом следует учитывать: – единство объемных, стоимостных, качественных, структурных факторов; – единство промежутков или моментов времени, за которые были исчислены сравниваемые показатели; – сопоставимость исходных условий производства (технических, природных и т. д.); – единый характер методики исчисления показателей и их состава. Выполнение большей части этих требований не вызывает затруднений, однако встречаются случаи, когда несопоставимость показателей не сразу бросается в глаза и, чтобы достичь ее, требуются дополнительные расчеты. Экономические явления имеют, как правило, количественную определенность, которая выражается в абсолютных и относительных величинах. Абсолютные величины показывают размеры явления в единицах меры, веса, объема, протяженности, стоимости и т. д., безотносительно к размерам других явлений. Относительные величины отражают соотношение величины изучаемого явления, величины какого-либо другого явления или величины этого явления, но взятой за другое время или по другому объекту. Относительные показатели получают в результате деления одной величины на другую, принимаемую за базу сравнения. Это могут быть данные плана, базисного года, другого предприятия, среднеотраслевые и т. д. Относительные величины выражаются коэффициентами (при базе 1) или в процентах (при базе 100). В экономическом анализе используются разные виды относительных величин: планового задания, выполнения плана, динамики, структуры, координации, интенсивности, эффективности. Не менее важное значение имеют в процессе анализа средние величины. Их «аналитическая сила» состоит в обобщении типичных, однородных показателей, явлений и процессов. Они позволяют переходить от единичного к общему, от случайного к закономерному. В экономическом анализе применяют, исходя из необходимости, различные формы средних – среднюю арифметическую, среднюю гармоническую, среднюю геометрическую, среднюю хронологическую, моду, медиану. Группировки – неотъемлемая часть почти любого экономического исследования. Они используются для определения наличия, направления и формы связи между изучаемыми показателями. Аналитическая группировка может быть качественной (атрибутивной) или количественной, в зависимости от признаков, на которых она основывается. По сложности построения различают два типа группировок: простые и комбинированные. С помощью простых группировок изучается взаимосвязь между явлениями, сгруппированными по какому-либо одному признаку. В комбинированных группировках такое деление осуществляется сначала по одному признаку, а потом внутри каждой группы – по другому признаку и т. д. Таким образом, могут быть построены двух-трехуровневые группировки. Они позволяют изучать разнообразные и сложные взаимосвязи. Однако следует отметить и их существенный недостаток: построение таких группировок весьма трудоемко, а полученные результаты трудно воспринимаются. Поэтому для изучения сложных взаимосвязей такую группировку лучше заменить несколькими простыми. Балансовый способ служит главным образом для отражения соотношений, пропорций двух групп взаимосвязанных и уравновешенных экономических показателей. Способ широко используется при анализе обеспеченности предприятия трудовыми, финансовыми ресурсами, сырьем, топливом, материалами, основными средствами и т. д., а также при анализе полноты их использования. Для определения платежеспособности предприятия используется платежный баланс, в котором соотносятся платежные средства и платежные обязательства. Как обязательное средство балансовый метод используется в экономическом анализе для проверки исходных сведений, на основе которых проводится анализ, а также для проверки правильности собственных аналитических расчетов (отклонение результативного показателя равно сумме изменений результативного показателя по факторам 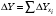 ). ).Графический способ представляет собой масштабное изображение показателей, чисел с помощью геометрических знаков (линий, прямоугольников, кругов) и служит наглядной иллюстрацией рассматриваемых явлений. Основные формы графиков, которые используются при анализе, – это диаграммы. По содержанию различают диаграммы сравнения, структурные, динамические, графики связи, графики контроля и т. д. 2 Способы факторного анализа Все явления и процессы хозяйственной деятельности предприятия находятся во взаимосвязи и взаимозависимости. Некоторые из них непосредственно связаны между собой, другие – косвенно. Каждое явление можно рассматривать и как причину, и как результат. Каждый результативный показатель зависит от многочисленных и разнообразных факторов. Чем более детально исследуется влияние факторов на величину результативного показателя, тем точнее результаты анализа и оценка качества работы предприятий. Под факторным анализом понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей. Все способы детерминированного факторного анализа основаны на приеме элиминирования. Элиминирование представляет собой логический прием, при помощи которого исключается влияние ряда факторов и выделяется какой-либо один фактор, являющийся объектом изучения. Детерминированный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т. е. результативный показатель может быть представлен в виде произведения, частного или алгебраической суммы факторов. При выполнении детерминированного факторного анализа необходимо выполнять ряд требований. 1. Факторы, которые включаются в модель, и сами модели должны иметь определенно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями. 2. Факторы, которые входят в систему, не только должны быть необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями. 3. Все показатели факторной модели должны быть количественно измеримыми, т. е. должны иметь единицу измерения и необходимую информационную обеспеченность. 4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов. Это значит, что в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя. Рекомендуется установить очередность элиминирования путем последовательного разложения результативного показателя по факторам или укрупнения факторов. При этом необходимо учитывать следующее: – если в формуле взаимосвязи показателей имеется несколько объемных факторов, то раньше других оценивают влияние факторов, характеризующих условия производства, а затем влияние структурных изменений и остальных качественных показателей; – промежуточные формулы, используемые для разложения сложного показателя по факторам, должны быть аналитичны (иметь реальное экономическое содержание). В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей. 1. Аддитивные модели: 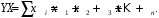 Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей. 2. Мультипликативные модели: 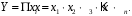 Этот тип модели применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов. 3. Кратные модели: 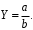 Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого. 4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей:  и т. д. и т. д.Выявление влияния факторов на изменение результативного показателя может быть определено с помощью различных методов. Способ цепных подстановок. Этот способ широко применяется на практике при функциональной прямой или обратной связи между факторами и результативным показателем. Сущность данного способа заключается в том, что, выявляя влияние отдельных факторов на общий результат, последовательно рассматривают каждый из влияющих факторов как переменный при неизменности остальных. Если результативный показатель является суммой факторов (аддитивная модель Y = a + b), то его изменение под воздействием каждого фактора находят как разницу между отчетной и базисной величинами фактора: DY(a) = Da; DY(b) = Db. Сумма найденных величин отклонений по факторам должна полностью соответствовать общему изменению результативного показателя: DY = Y1 – Y0 = DY(a) + DY(b). Если рассматриваемый показатель равен произведению двух факторов (мультипликативная модель Y = a b), то применяют следующее правило. Факторы обязательно нужно подразделить на объемный (количественный) и качественный. К количественным относят абсолютные показатели и средние хронологические величины, получаемые на их базе (среднесуточная погрузка в вагонах, работа дороги и т. д.). Важнейшим признаком количественных показателей является возможность суммирования отдельных показателей, рассчитанных внутри совокупности. Качественные показатели, как правило, характеризуют общее для всех единиц совокупности свойство, они не суммируются (средняя статическая нагрузка на вагон, средняя дальность перевозки, себестоимость перевозок и т. д.). Для оценки влияния на величину сложного показателя изменений любого фактора необходимо вычислить две условные величины этого показателя – две подстановки. В первой подстановке за фактор, влияние которого изучается, берется отчетный. Во второй подстановке этот фактор остается базисным. При этом полагают, что остальные показатели остались неизменными. При определении влияния количественного показателя значение качественного фактора принимается по его базисной величине. Влияние качественных факторов устанавливается только при отчетных количественных показателях. Размер влияния фактора определяется путем вычитания из последующей подстановки предыдущей (из второй – первой, из третьей – второй и т. д.). В первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Рассмотрим расчет влияния факторов на изменение результативного показателя в модели Y = a × b, где Y – результативный анализируемый показатель; а – количественный фактор; b – качественный фактор. Расчет результативного показателя за базисный период: Y0 = a0 × b0. Расчет первой подстановки путем замены базисного значения количественного фактора на его текущее значение: Yусл1 = a1× b0. Определение влияния на результативный показатель количественного фактора: DY(a) = Yусл1 – Y0 = a1× b0 – a0 × b0 = (a1 – a0) × b0. Расчет второй подстановки путем замены базисного значения качественного фактора его текущим значением: Yусл2 = a1 · b1. Определение влияния на результативный показатель качественного фактора: DY(b) = Yусл2 – Yусл1 = a1b1 – a1 · b0 = (b1 – b0) · a1. Сумма найденных величин отклонений по факторам должна полностью соответствовать общему изменению результативного показателя: DY = Y1 – Y0 = DY(a) + DY(b). В случае, когда рассматриваемый показатель является функцией не двух, а большего числа переменных, то из этой функции нужно выделить ведущий качественный фактор, а оставшаяся часть функции рассматривается как один объемный фактор, имеющий определенное экономическое содержание. Затем применяют сформулированное выше правило для случая с двумя переменными. Далее аналогичным образом рассматривают оставшуюся часть функции и выполняют последующие подстановки, пока не будет выявлено изменение результативного показателя под воздействием всех влияющих факторов. Рассмотрим расчет влияния факторов на изменение результативного показателя в модели Y = a× (b+ с), где Y – результативный анализируемый показатель; а – количественный фактор; b и с – качественные факторы. Расчет результативного показателя за базисный период: Y0 = a0 × (b0 + с0). Расчет первой подстановки путем замены базисного значения количественного фактора на его текущее значение: Yусл1 = a1 × (b0 + с0). Определение влияния на результативный показатель количественного фактора: DY(a) = Yусл1 – Y0. Расчет второй подстановки путем замены базисного значения качественного фактора b его текущим значением: Yусл2 = a1× (b1 + с0). Определение влияния на результативный показатель качественного фактора b: DY(b) = Yусл2 – Yусл1. Расчет третьей подстановки путем замены базисного значения качественного фактора с его текущим значением: Yусл3 = a1× (b1 + с1) = Y1. Определение влияния на результативный показатель качественного фактора с: DY(c) = Yусл3 – Yусл2. Сумма найденных величин отклонений по факторам должна полностью соответствовать общему изменению результативного показателя: DY = Y1 – Y0 = DY(a) + DY(b)+ DY(c). Способ абсолютных разниц. Способ абсолютных разниц является одной из модификаций метода цепных подстановок. Как и способ цепных подстановок, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных моделях и смешанных – типа  . Несмотря на его ограниченное использование, этот способ нашел широкое применение в экономическом анализе благодаря своей простоте. . Несмотря на его ограниченное использование, этот способ нашел широкое применение в экономическом анализе благодаря своей простоте.При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели, где факторы ранжированы. Рассмотрим алгоритм расчета для мультипликативной факторной модели типа  . Имеются плановые и фактические значения по каждому факторному показателю, а также их абсолютные отклонения: . Имеются плановые и фактические значения по каждому факторному показателю, а также их абсолютные отклонения: Определим изменение величины результативного показателя за счет каждого фактора: 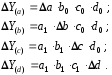 Алгоритм расчета факторов этим способом в смешанных моделях типа 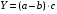 будет иметь следующий вид: будет иметь следующий вид: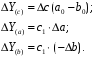 Способ корректировок. Он незначительно отличается от способа подстановок. Отличие – в порядке расчета подстановки. Для расчета подстановки базисную величину результативного показателя умножают на корректировочный коэффициент 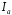 . Корректировочный коэффициент представляет собой отношение отчетного значения показателя, принятого для корректировки, к базисному (чаще всего этот показатель характеризует объем работы): . Корректировочный коэффициент представляет собой отношение отчетного значения показателя, принятого для корректировки, к базисному (чаще всего этот показатель характеризует объем работы):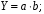 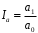 , ,где 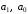 – объемные показатели соответственно за текущий и базисный периоды. – объемные показатели соответственно за текущий и базисный периоды.Влияние факторов на результативный показатель определяется следующим образом: 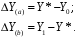 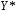 – подстановка – определяется: – подстановка – определяется: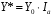 . .Проверка правильности расчетов: 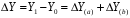 , ,где 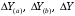 – соответственно изменение результативного показателя под влиянием факторов соответственно объемного а, качественного b и общее изменение; – соответственно изменение результативного показателя под влиянием факторов соответственно объемного а, качественного b и общее изменение;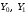 – базисное и текущее значения результативного показателя. – базисное и текущее значения результативного показателя.Способ относительных величин (коэффициентов). Способ применяется в тех случаях, когда исходная информация для анализа представлена относительными величинами и не требуется высокой точности расчетов. Необходимым условием применения этого способа является зависимость результативного показателя только от двух факторов: – для мультипликативных моделей – 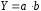 ; ;– аддитивных моделей – 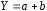 ; ;– кратных моделей – 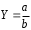 . .Исходя из теории индексов можно вывести следующие правила: темпы прироста показателей для мультипликативных моделей приближенно равны сумме темпов прироста сомножителей, а именно: 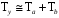 , ,где  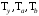 – темпы прироста показателей y, a, b, %; – темпы прироста показателей y, a, b, %;темпы прироста показателей для аддитивной модели равны сумме темпов прироста слагаемых показателей, взвешенных по соответствующим удельным весам: 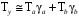 , ,где 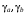 – удельный вес или доля величины показателя соответственно а, b в общей величине показателя Y. – удельный вес или доля величины показателя соответственно а, b в общей величине показателя Y.В расчетные формулы темпы прироста подставляются всегда в процентах, а удельные веса – в долях; темпы прироста показателей для кратной модели приближенно равны разности темпов прироста числителя и знаменателя формулы, а именно: 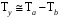 . .Способ пропорционального деления и долевого участия. Этот способ в ряде случаев может быть использован для определения величины влияния факторов на прирост результативного показателя. Это касается тех случаев, когда имеют дело с аддитивными моделями типа 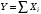 и смешанными типа и смешанными типа 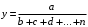 . .В первом случае при одноуровневой модели типа 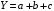 расчет производится следующим образом: расчет производится следующим образом: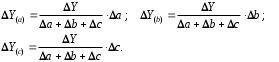 Методика расчета для смешанных моделей несколько сложнее. Когда известны 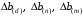 , а также , а также 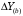 , то для определения , то для определения 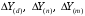 можно использовать способ пропорционального деления, который основан на пропорциональном распределении прироста результативного показателя Y за счет изменения фактора b между факторами второго уровня d, n, m соответственно их величине. Пропорциональность этого распределения достигается путем определения постоянного для всех факторов коэффициента, который показывает величину изменения результативного показателя Y за счет изменения фактора b на единицу. можно использовать способ пропорционального деления, который основан на пропорциональном распределении прироста результативного показателя Y за счет изменения фактора b между факторами второго уровня d, n, m соответственно их величине. Пропорциональность этого распределения достигается путем определения постоянного для всех факторов коэффициента, который показывает величину изменения результативного показателя Y за счет изменения фактора b на единицу.Величина коэффициента К определяется следующим образом: 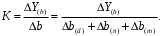 Умножив этот коэффициент на абсолютное отклонение b за счет соответствующего фактора, найдем отклонения результативного показателя: 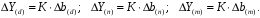 Для решения такого типа задач можно использовать также способ долевого участия. Для этого сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя: 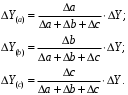 Способ структурных сдвигов. Способ применяется при анализе качественных показателей, зависящих от состава (структуры) изучаемых явлений. Величина качественных показателей выражается формулой взаимосвязи как сумма произведений структурных коэффициентов 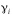 на частные качественные факторы на частные качественные факторы 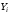 : : 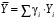 . .Например, средняя статическая нагрузка зависит от породовой структуры грузов и статических нагрузок каждого рода грузов; средняя дальность перевозки одной тонны груза зависит от структуры перевозимых грузов, дальности перевозки каждого рода груза и т. п. Для анализа изменений результативного качественного показателя рассчитывают его условную величину – подстановку, в которой структурные коэффициенты принимаются на отчетном, а частные качественные факторы – на базисном уровнях: 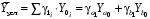 , ,где 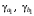 – фактическая структура изучаемого явления; – фактическая структура изучаемого явления;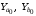 – базовое значение частных факторов. – базовое значение частных факторов.Влияние на результативный показатель структурных сдвигов оценивают при сравнении подстановки с базисной величиной результативного показателя, а влияние частных качественных факторов – при сравнении отчетной величины результативного показателя и подстановки: 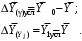 При расчетах по вышеприведенным формулам получена оценка одновременного изменения всех частных качественных факторов. Чтобы выделить влияние каждого из этих факторов, их изменения умножают на отчетный уровень соответствующего структурного коэффициента: 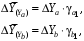 причем 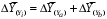 . .Для оценки структурных изменений необходимо изменение данного структурного коэффициента умножить на разность между базисными величинами соответствующего частного качественного фактора и результативного качественного показателя: 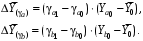 Оценив причины изменений сложного показателя, можно определить влияние этих причин на связанный с ним результативный показатель V. Поскольку 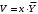 , то можно записать: , то можно записать: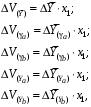 при этом должно соблюдаться равенство 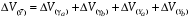 . .Элиминирование как способ детерминированного факторного анализа имеет существенный недостаток. При его использовании исходят из того, что факторы изменяются независимо друг от друга. На самом деле они изменяются совместно, взаимосвязанно, и от этого взаимодействия получается дополнительный прирост результативного показателя (неразложимый остаток), который при применении элиминирования присоединяется к одному из факторов, как правило, к показателю, анализируемому в последнюю очередь. В связи с этим величина влияния факторов на изменение результативного показателя меняется в зависимости от места, на которое поставлен тот или иной фактор в детерминированной модели. В последнее время применяются и другие способы факторного анализа, упрощающие расчеты и дающие более точное распределение приращения результативного показателя между факторами: интегральный, метод взвешенных конечных разностей, логарифмический, кольцевой и экстремальный. Логарифмический способ. Этот способ позволяет достаточно точно распределить приращение сложного показателя между влияющими факторами. Сущность его заключается в логарифмировании обеих частей формулы взаимосвязи сложного показателя с факторами с целью замены произведения или частного от деления факторов суммой их логарифмов. Допустим, сложный показатель Y определяется в общем виде по формуле 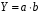 . .Изменение результативного показателя и влияющих факторов определяется следующим образом: 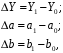 где 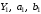 – фактические значения сложного показателя и факторов; – фактические значения сложного показателя и факторов;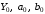 – базисные значения сложного показателя и факторов. – базисные значения сложного показателя и факторов.Задача состоит в определении того, какую часть от 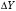 составляет влияние a и b, при этом должно соблюдаться условие: составляет влияние a и b, при этом должно соблюдаться условие: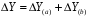 . .Эту зависимость можно представить как произведение индексов: 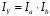 или или 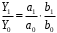 . .Прологарифмировав обе части выражения, получим: 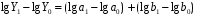 . .Из этого выражения можно найти значение коэффициентов, определяющих влияние каждого фактора на сложный показатель Y: 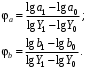 Отсюда часть абсолютного приращения сложного показателя 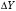 за счет i-го влияющего фактора рассчитывается следующим образом: за счет i-го влияющего фактора рассчитывается следующим образом: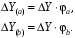 Логарифмический способ факторного анализа не имеет недостатков традиционных способов элиминирования, но имеет свои. Главные недостатки данного способа: во-первых, невозможность определить влияние факторов на сложный показатель в том случае, когда факторы изменяются не в одном направлении (одни увеличиваются, другие уменьшаются, а общее приращение становится равным или близким к нулю); во-вторых, возможность применять этот способ только при анализе мультипликативных моделей. Экстремальный способцелесообразен при малом числе факторов и небольших приращениях, а также для ускорения расчетов. Сущность данного способа заключается в исчислении средних по максимальному и минимальному значениям приращений сложного показателя, приходящихся на каждый фактор. Из анализа результатов расчетов способом разниц зависимостей мультипликативного типа по всем возможным вариантам замечено, что при положительных приращениях минимальные значения частей изменения общего показателя, приходящиеся на каждый фактор, получаются тогда, когда значения этого фактора записаны в первой строке, а максимальные – когда эти значения записаны в последней строке. Например, при трех влияющих факторах ( 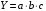 ) можно выбрать следующие экстремальные значения: ) можно выбрать следующие экстремальные значения: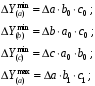 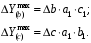 Отсюда можно получить расчетную формулу для экстремального способа: 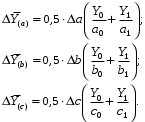 Для более высокой точности и при большом количестве факторов, имеющих приращения с разными знаками, применяется кольцевой способ; если факторы имеют приращения с одним знаком – то логарифмический. 3 Стохастические связи в анализе финансово-хозяйственной деятельности Методы решения экономических задач с использованием математики и кибернетики называют экономико-математическими методами. К ним относят экономико-статистические методы, эконометрические, методы оптимальных решений, экономическую кибернетику. На практике далеко не все экономические явления и процессы могут изучаться с помощью способов детерминированного факторного анализа, так как в большей части случаев их нельзя свести к таким функциональным зависимостям, когда величине факторного показателя соответствует единственная величина результативного показателя. Чаще в экономических исследованиях встречаются стохастические зависимости, которые отличаются приблизительностью, неопределенностью. Они проявляются только в среднем по значительному количеству объектов (наблюдений). Здесь каждой величине факторного показателя (аргумента) может соответствовать несколько значений результативного показателя (функции). Такого рода зависимости изучаются с помощью корреляционно-регрессионного анализа. Корреляционная (стохастическая) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений. Различают парную и множественную корреляцию. Парная корреляция – это связь между двумя показателями, один из которых является факторным, а другой – результативным. Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем. Наиболее широкое применение в экономических исследованиях нашли приемы корреляционного анализа, которые позволяют количественно выразить взаимосвязь между показателями. Необходимые условия применения корреляционного анализа: 1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов). 2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации. Применение корреляционного анализа позволяет: – определить изменение результативного показателя под воздействием одного или нескольких факторов (в абсолютном измерении), т. е. определить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу; – установить относительную степень зависимости результативного показателя от каждого фактора. Исследование корреляционных соотношений имеет огромное значение в анализе хозяйственной деятельности: устанавливаются место и роль каждого фактора в формировании уровня исследуемых показателей, углубляются знания об изучаемых явлениях, определяются закономерности их развития и, таким образом, точнее обосновываются планы и управленческие решения, более объективно оцениваются итоги деятельности предприятий и более полно определяются внутрихозяйственные резервы. Одна из основных задач корреляционного анализа – определение влияния факторов на величину результативного показателя (в абсолютном измерении). Для решения этой задачи подбирается соответствующий тип математического уравнения, которое наилучшим образом отражает характер изучаемой связи (прямолинейной, криволинейной и т. д.). Это играет важную роль в корреляционном анализе, потому что от правильного выбора уравнения регрессии зависит ход решения задачи и результаты расчетов. Обоснование уравнения связи делается с помощью сопоставления параллельных рядов, группировки данных и линейных графиков. Размещение точек на графике покажет, какая зависимость образовалась между изучаемыми показателями – прямолинейная или криволинейная. Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой: 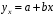 , ,где x – факторный показатель; 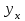 – результативный показатель; – результативный показатель; a и b – параметры уравнения регрессии, которые требуется определить. Это уравнение описывает такую связь между двумя признаками, при которой с изменением факторного показателя на определенную величину наблюдается равномерное возрастание или убывание значений результативного показателя. Значения коэффициентов a и bнаходят из системы уравнений, полученных по способу наименьших квадратов. В данном случае система уравнений имеет следующий вид: 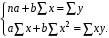 Коэффициентa – постоянная величина результативного показателя, которая не связана с изменением данного фактора. Параметр bпоказывает среднее изменение результативного показателя с повышением или понижением величины фактора на единицу его измерения. Используя тот или иной тип математического уравнения, можно определить степень зависимости между изучаемыми явлениями, т. е. узнать, на сколько единиц в абсолютном измерении изменяется величина результативного показателя с изменением факторного на единицу. Однако регрессионный анализ не дает ответа на вопрос, тесная это связь или нет, решающее воздействие оказывает данный фактор на величину результативного показателя или второстепенное. Для измерения тесноты связи между факторными и результативными показателями используется коэффициент корреляции. В случае прямолинейной формы связи между изучаемыми показателями коэффициент корреляции, r, рассчитывается по следующей формуле: 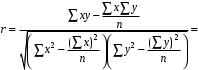 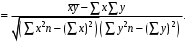 Коэффициент корреляции может принимать значения от 0 до ± 1. Чем ближе его величина к единице, тем более тесная связь между изучаемыми явлениями, и наоборот, знак показывает направление связи между фактором и результативным показателем. Чтобы установить, насколько тесной является связь при криволинейной форме зависимости, используется не линейный коэффициент корреляции, а корреляционное отношение: 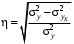 , ,где 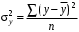 ; ; 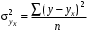 . .Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества факторов. Как правило, каждый фактор в отдельности не определяет изучаемое явление во всей полноте. Только комплекс факторов в их взаимосвязи может дать более или менее полное представление о характере изучаемого явления. Многофакторный корреляционный анализ состоит из нескольких этапов. На первом этапе определяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются наиболее существенные из них для корреляционного анализа. На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа. На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т. е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. На четвертом этапе проводится расчет основных показателей связи корреляционного анализа. На пятом этапе дается статистическая оценка результатов корреляционного анализа и предлагается способ их практического применения. Отбор факторов для корреляционного анализа является очень важным моментом в экономическом анализе. От того, насколько правильно сделан отбор факторов, зависит точность выводов по итогам анализа. Важное значение при отборе факторов имеют и теория и практика. При этом необходимо придерживаться следующих правил. 1. При отборе факторов в первую очередь следует учитывать причинно-следственные связи между показателями, так как только они раскрывают сущность изучаемых явлений. Анализ факторов, которые находятся только в математических соотношениях с результативным показателем, не имеет практического смысла. 2. При создании многофакторной корреляционной модели необходимо отбирать самые значимые факторы, которые оказывают решающее воздействие на результативный показатель, так как охватить все условия и обстоятельства практически невозможно. Факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет. 3. Все факторы должны быть количественно измеримы, т. е. иметь единицу измерения, и информация о них должна содержаться в учете и отчетности. 4. В корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер. 5. Не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа. 6. Нельзя включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер. Большую помощь при отборе факторов для корреляционной модели оказывают аналитические группировки, способ сравнения параллельных и динамических рядов, линейные графики. Первые два этапа включают в себя сбор и статистическую оценку исходной информации, которая будет использоваться при корреляционном анализе. Собранная исходная информация должна быть проверена на точность, однородность и соответствие закону нормального распределения. В первую очередь необходимо убедиться в достоверности информации, насколько она соответствует объективной действительности. Использование недостоверной, неточной информации приведет к неправильным результатам анализа и неправильным выводам. Одно из условий корреляционного анализа – однородность исследуемой информации относительно распределения ее около среднего уровня. Если в совокупности имеются группы объектов, которые значительно отличаются от среднего уровня, то это говорит о неоднородности исходной информации. Критериями однородности информации служат среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю. Среднеквадратическое отклонение показывает абсолютное отклонение индивидуальных значений от среднеарифметической величины. Оно определяется по формуле: 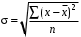 . .Коэффициент вариации показывает относительную меру отклонения отдельных значений от среднеарифметической. Он рассчитывается по формуле: 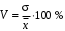 . .Следующий этап корреляционного анализа – расчет уравнения связи (регрессии). Решение проводится обычно шаговым способом. Сначала в расчет принимается один фактор, оказывающий наиболее значимое влияние на результативный показатель, потом второй, третий и т. д. И на каждом шаге рассчитываются уравнение связи, множественный коэффициент корреляции и детерминации, F-отношение (критерий Фишера), стандартная ошибка и другие показатели, с помощью которых оценивается надежность уравнения связи: 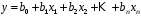 . .Коэффициенты регрессии в уравнении связи имеют разные единицы измерения, что делает их несопоставимыми, если возникает вопрос о сравнительной силе воздействия факторов на результативный показатель. Чтобы привести их в сопоставимый вид, все переменные уравнения регрессии выражают в долях среднеквадратического отклонения, другими словами, рассчитывают стандартизированные коэффициенты регрессии. Их еще называют бета-коэффициентами по символу, который принят для их обозначения ( 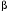 ). ). Бета-коэффициенты и коэффициенты регрессии связаны следующим отношением: 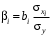 . .Бета-коэффициенты показывают, что если величина фактора увеличится на одно среднеквадратическое отклонение, то соответствующая зависимая переменная увеличится или уменьшится на долю своего среднеквадратического отклонения. Сопоставление бета-коэффициентов позволяет сделать вывод о сравнительной степени воздействия каждого фактора на величину результативного показателя. По аналогии можно сопоставить и коэффициенты эластичности, которые рассчитываются по формуле: 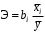 . .Коэффициенты эластичности показывают, на сколько процентов в среднем изменяется функция с изменением аргумента на 1 %. Чтобы убедиться в точности (надежности) уравнения связи и правомерности его использования для практической цели, необходимо дать статистическую оценку надежности показателей связи. Для этого используются критерий Фишера (F-отношение), средняя ошибка аппроксимации ( 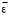 ), коэффициенты множественной корреляции (R) и детерминации (Д). ), коэффициенты множественной корреляции (R) и детерминации (Д). Критерий Фишера рассчитывается следующим образом: 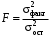 , ,где 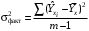 – факторная дисперсия; – факторная дисперсия;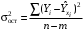 – остаточная дисперсия; – остаточная дисперсия;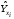 – индивидуальные значения результативного показателя, рассчитанные по уравнению; – индивидуальные значения результативного показателя, рассчитанные по уравнению;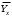 – среднее значение результативного показателя, рассчитанное по уравнению; – среднее значение результативного показателя, рассчитанное по уравнению;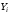 – фактические индивидуальные значения результативного показателя; – фактические индивидуальные значения результативного показателя;m – количество параметров в уравнении связи с учетом свободных членов уравнения; n – количество наблюдений. Фактическая величина F-отношения сопоставляется с табличной и делается заключение о надежности связи. Если 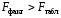 , то гипотеза об отсутствии связи между результативным показателем и исследуемыми факторами отклоняется. , то гипотеза об отсутствии связи между результативным показателем и исследуемыми факторами отклоняется.Для статистической оценки точности уравнения связи используется также средняя ошибка аппроксимации:   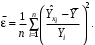 Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпирической), тем меньше средняя ошибка аппроксимации. О полноте связи можно судить также по величине множественных коэффициентов корреляции (R) и детерминации (Д): 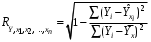 ; ;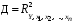 . .После проверки надежности рассчитанного уравнения регрессии делается вывод о возможности его использования на практике: 1. Для оценки результатов хозяйствования путем сравнения фактической величины результативного показателя с теоретической (расчетной), которая определяется на основе уравнения множественной регрессии. Если 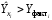 , то это говорит о том, что данное предприятие использует свои возможности несколько хуже, чем в среднем все исследуемые предприятия. , то это говорит о том, что данное предприятие использует свои возможности несколько хуже, чем в среднем все исследуемые предприятия.2. Для расчета влияния факторов на прирост результативного показателя 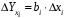 , ,где 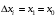 ; ;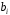 – коэффициент уравнения регрессии. – коэффициент уравнения регрессии.3. Для подсчета резервов повышения уровня исследуемого показателя ( 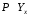 ) на величину соответствующего коэффициента регрессии ) на величину соответствующего коэффициента регрессии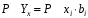 , ,где 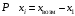 . .4. Для прогнозирования и планирования уровня результативного показателя. С этой целью необходимо в полученное уравнение связи подставить плановый (прогнозный) уровень факторных показателей. Таким образом, многофакторный корреляционный анализ имеет важную научную и практическую значимость. Он позволяет изучить закономерности изменения результативного показателя в зависимости от поведения разных факторов, определить их влияние на величину результативного показателя, установить, какие из них являются основными, а какие второстепенными. Этим достигается более объективная оценка деятельности предприятия, более точное и полное определение внутрихозяйственных резервов. Литература: Комплексный анализ хозяйственной деятельности: учебник и практикум для студентов, обучающихся по экономическим направлениям и специальностям и направлению "Экономика" / [В. И. Бариленко и др.] ; под редакцией В. И. Бариленко ; Финансовый университет при Правительстве Российской Федерации. - Москва: Юрайт, 2015. - 455 с. Савицкая Г.В. Экономический анализ: Учебник. - 14-е изд., перераб. и доп. - М. : Инфра-М, 2016. - 649 с. – (Высшее образование: Бакалавриат). |
