Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара

• Название: Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара
• Дата: 11.02.2022
• Размер: 5.37 Mb.
• Имя файла: Savchenko_Lektsii_Nachertatelnaya_geometriya.doc
• Тип: Конспект; #358523
• страница: 11 из 20

Лекция 5

4. ПЕРПЕНДИКУЛЯРНОСТЬ ГЕОМЕТРИЧЕКСКИХ ОБЪЕКТОВ

4.1. Проецирование прямого угла

В общем случае плоский угол проецируется на плоскость проекций с искажением.

Возьмем две прямые общего положения l и k. Прямая l пересекает горизонтальную плоскость проекций под углом a, а прямая k – под углом a¢. Между собой прямые пересекаются под произвольным углом j. Прямоугольная проекция угла j₁ определяется по формуле: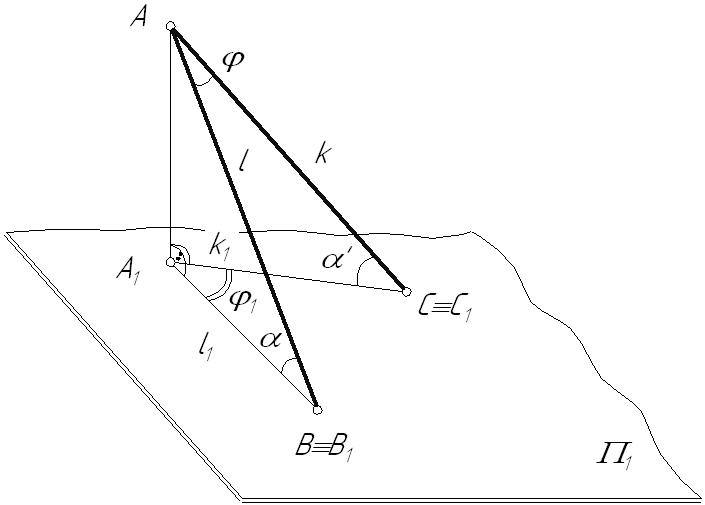

.



Рис. 4.1

Пусть , , тогда при .

.

При , , следовательно, .

Теорема о проецировании прямого угла:

Прямой угол на плоскость проекций проецируется без искажения, если, по крайней мере, один из его лучей параллелен этой плоскости проекций.

Пусть прямые l(АВ) и k(АС) пересекаются под прямым углом. Прямая l параллельна горизонтальной плоскости проекций. Тогда: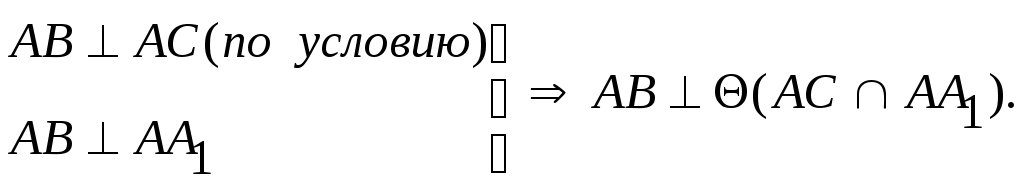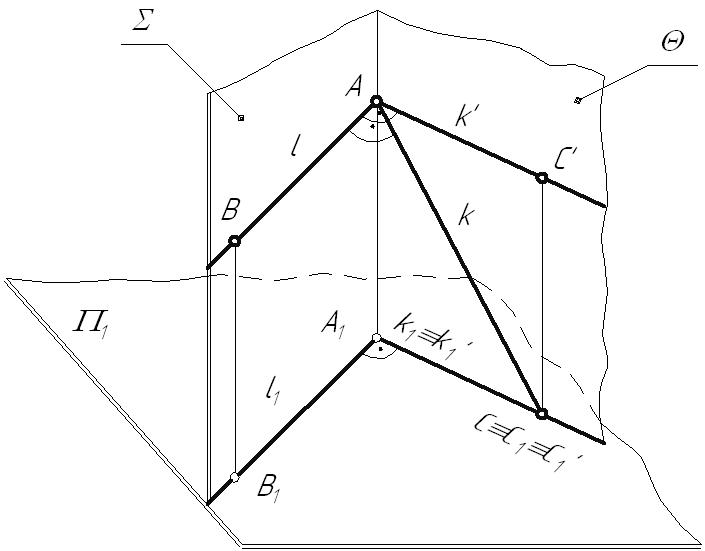

1. 
   .
   
2. 
   .
   

Рис. 4.2

Все прямые, лежащие в плоскости , на горизонтальную плоскость проекций проецируются перпендикулярно следу плоскости .

Пример: Построить перпендикуляр из точки А к горизонтали.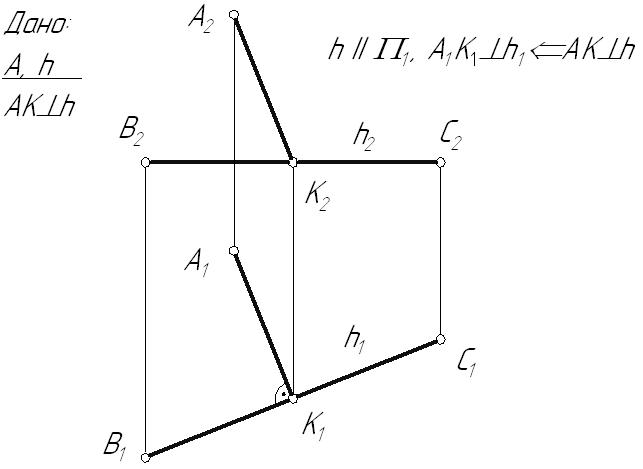



Рис. 4.3

4.2. Линия наибольшего наклона плоскости

Прямая, лежащая в плоскости и образующая с плоскостью проекций наибольший угол, называется линией наибольшего наклона плоскости.

Линии наибольшего наклона перпендикулярны к соответствующим линиям уровня плоскости.

Угол между линией наибольшего наклона и плоскостью проекций равен углу наклона самой плоскости к этой плоскости проекций. Поэтому с помощью этой линии определяют двухгранные углы между заданной плоскостью и соответствующими плоскостями проекций.

Теорема:

Прямые, лежащие в плоскости и перпендикулярные соответствующим линиям уровня плоскости, являются линиями наибольшего наклона.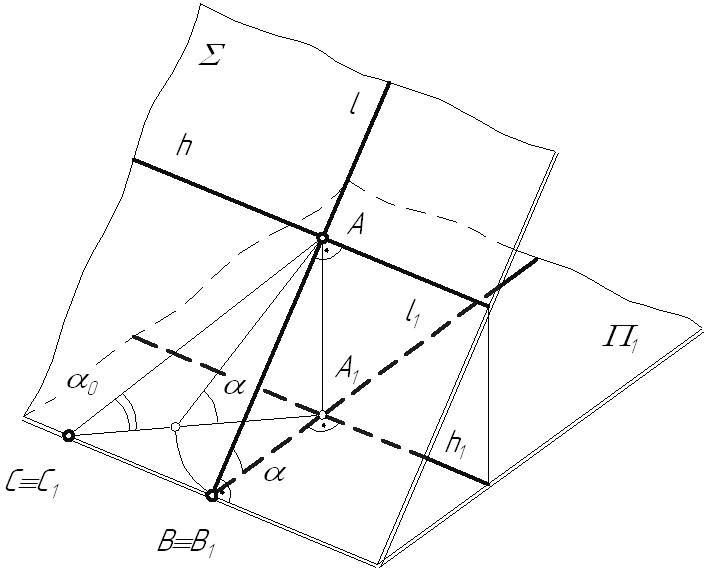

Рис. 4.4

Возьмем плоскость общего положения , наклоненную под углом к горизонтальной плоскости проекций . Проведем в ней горизонталь h и две линии общего положения – прямую АВ, перпендикулярную горизонтали, и произвольно наклоненную прямую АС.

В результате построений угол прямой. Линию АВ повернем вокруг проецирующего луча до совмещения с плоскостью угла . Из рисунка видно, что . Значит, прямая АВ наклонена к плоскости проекций под большим углом. Поэтому именно она называется линией наибольшего наклона.

Пример: Определить действительную величину угла наклона плоскости 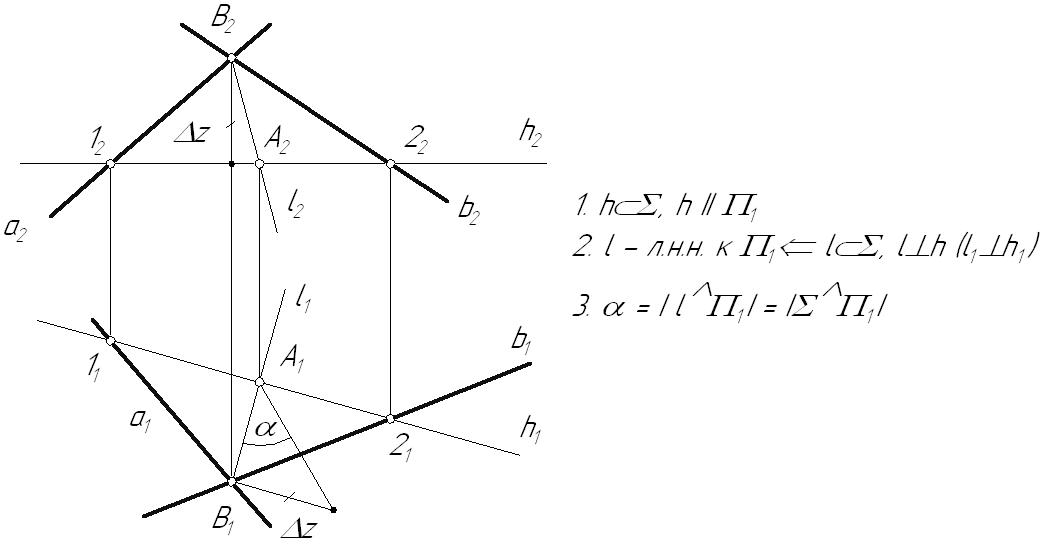к горизонтальной плоскости проекций.



Рис. 4.5

Аналогично находятся углы наклона плоскости к фронтальной и профильной плоскостям проекций. Л.н.н. к фронтальной плоскости проекций перпендикулярна фронтали плоскости, а л.н.н. к профильной плоскости проекций – профильной прямой плоскости.