Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара

• Название: Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара
• Дата: 11.02.2022
• Размер: 5.37 Mb.
• Имя файла: Savchenko_Lektsii_Nachertatelnaya_geometriya.doc
• Тип: Конспект; #358523
• страница: 19 из 20

6.8. Пересечение поверхностей

6.8.1. Пересечение многогранников

Многогранники пересекаются по замкнутым пространственным ломаным линиям, которые могут быть найдены следующим образом:

1. 
   Способ ребер. Находятся точки пересечения ребер одного многогранника с гранями другого.
   
2. 
   Способ граней. Определяются отрезки прямых, по которым грани одного многогранника пересекаются с гранями другого.
   

Пример: Построить линию пересечения двух трехгранных призм, одна из которых проецирующая.

В результате пересечения заданных многогранников получается ломаная пространственная линии. Она соединяет соответствующие точки пересечения ребер одного многогранника с гранями другого. Так как одна из призм проецирующая относительно горизонтальной плоскости проекций, горизонтальная проекция линии пересечения совпадает с горизонтальным очерком этой призмы. Искомые точки сечения можно получить, решая задачу на пересечение прямой (ребра) с плоскостью (гранью).

, .

, .

Для построения точек пересечения ребра b с гранями призмы, используется горизонтально-проецирующая плоскость .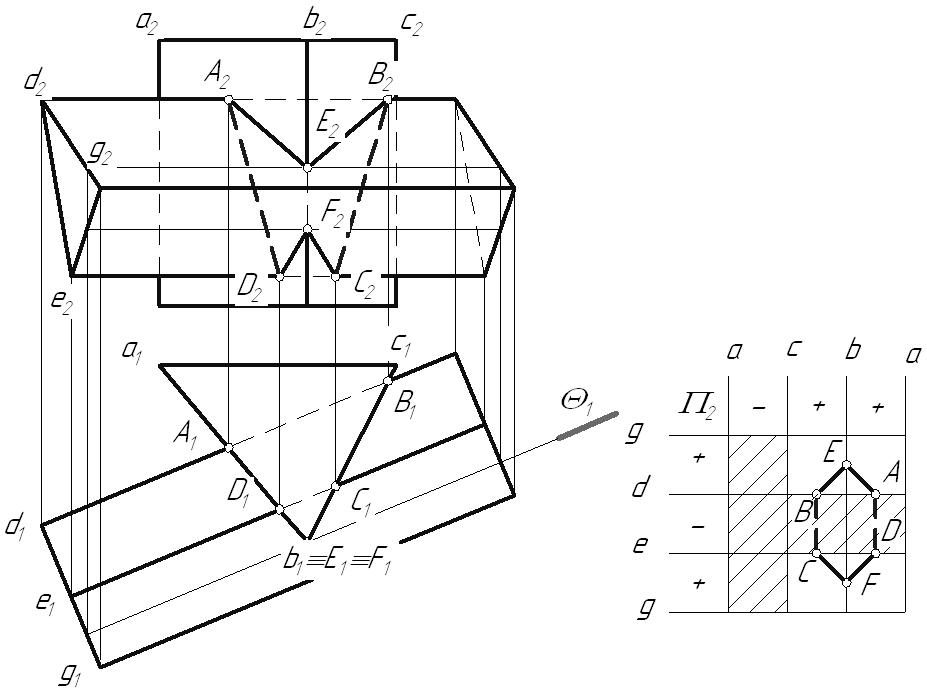
.

.



Рис. 6.18

Для определения видимости линии сечения строится диаграмма, на которой схематично в произвольных размерах изображаются грани заданных призм. Знаками  и  отмечается видимость граней многогранников. На соответствующих гранях и ребрах наносятся точки сечения, и соединяют их с учетом видимости. Видимыми считаются те звенья линии пересечения, которые лежат на видимых гранях обоих многогранников.

Лекция 11

6.8.2. Пересечение поверхностей вращения

Линией пересечения поверхностей является плоская или пространственная кривая, состоящая из:

• 
  одного замкнутого контура, если одно геометрическое тело частично врезается в поверхность другого;
  
• 
  распадается на несколько линий, если поверхность одного тела полностью пронизывает поверхность другого.
  

Рассмотрим особые случаи пересечения поверхностей вращения.

Цилиндрические, конические поверхности и однополосный гиперболоид вращения относятся к линейчатым поверхностям вращения второго порядка. Сфера, эллипсоид вращения, параболоид вращения и двухполосный гиперболоид вращения – нелинейчатые поверхностям второго порядка.

Поверхность второго порядка – множество точек пространства, декартовые координаты которых соответствуют алгебраическому уравнению второй степени.

.

Из аналитической геометрии известно, что порядок линии пересечения поверхностей равен произведению порядков поверхностей. Поэтому в общем случае две поверхности второго порядка (квадрики) пересекаются по пространственной линии четвертого порядка (биквадратной кривой), которая иногда распадается на несколько линий.

В некоторых частных случаях линия пересечения распадается на две плоские кривые второго порядка. Условия, при которых это возможно, определены в следующих теоремах. Зная их, можно быстрее и точнее построить линию пересечения поверхностей.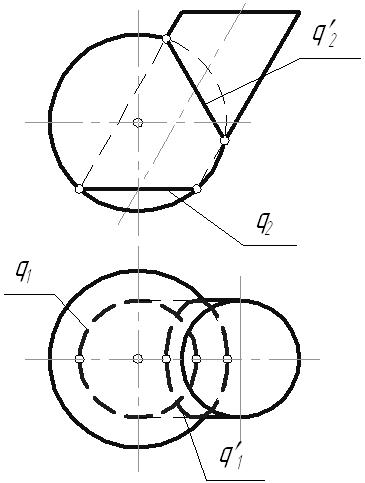

Рис. 6.19
Теорема 1:

Если две квадрики пересекаются по одной плоской кривой, то существует и другая плоская кривая, по которой они пересекаются.
Например, линия пересечения сферы и эллиптического цилиндра с круговым основанием распадается на две коники – окружности (q, q).

Теорема 2:

Если две квадрики имеют касание в двух точках, то линия их пересечения распадается на две коники, плоскости которых проходят через отрезок прямой, соединяющей эти точки.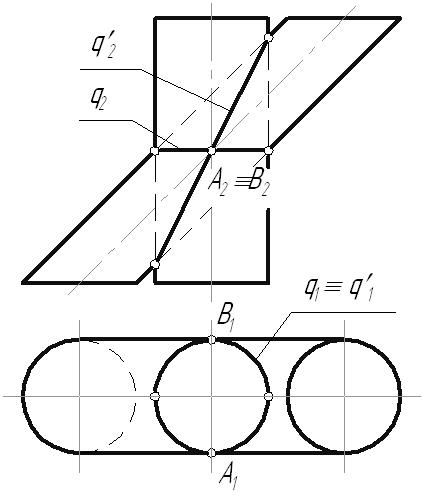

Рис. 6.20


Поверхности прямого кругового цилиндра и эллиптического цилиндра с круговым основанием имеют две общие точки касания (А, В). Следовательно, по Т2 они пересекаются по двум коникам – окружности (q) и эллипсу (q), плоскости которых пересекаются по прямой АВ.

Теорема 3:

Две соосные поверхности вращения пересекаются по окружностям-параллелям, число которых равно числу точек пересечения главных полумеридианов поверхностей.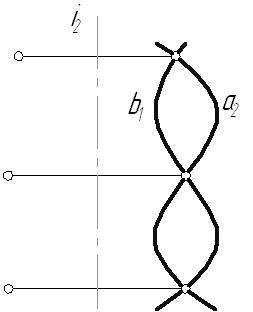

Рис. 6.21
Соосными называются поверхности, имеющие общую ось вращения.

Так как плоскость сечения перпендикулярна оси вращения i, линия сечения (окружность) проецируется:

• 
  в окружность на плоскость, перпендикулярную оси i;
  
• 
  в отрезок прямой – на плоскость, параллельную оси i;
  
• 
  в эллипс – на любую другую плоскость.
  

Эти особенности соосных поверхностей вращения позволяют использовать их, в частности сферу, в качестве посредников при построении линии пересечения поверхностей вращения. Любая поверхность вращения, ось которой проходит через центр сферы, соосна с ней и, следовательно, пересекает ее по окружности.

Теорема 4 (Теорема Монжа):

Если две поверхности второго порядка (квадрики) описаны вокруг третьей квадрики, то они пересекаются по двум плоским кривым второго порядка (коникам).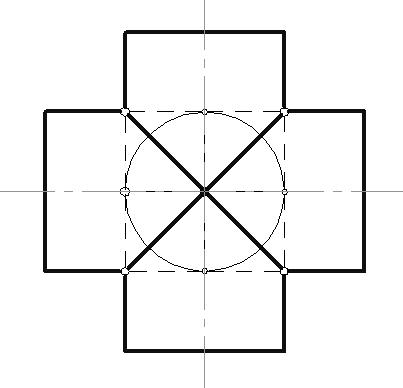

Рис. 6.22


В соответствии с этой теоремой, линии пересечения поверхностей, описанных около сферы, будут плоскими кривыми – эллипсами.

Построение линии пересечения поверхностей вращения в общем случае ведется с помощью дополнительных секущих поверхностей, в качестве которых могут быть использованы плоскости или сферы.

Секущие поверхности выбираются таким образом, чтобы с заданными поверхностями они пересекались по линиям, легко определяемым на КЧ.

Чтобы построить линию пересечения поверхностей на КЧ, необходимо:

1. 
   Ввести ряд вспомогательных плоскостей или сфер, пересекающих обе заданные поверхности.
   
2. 
   Построить линию пересечения каждой заданной поверхности со вспомогательной.
   
3. 
   В месте пересечения построенных таким образом линий определить точки искомой линии взаимного пересечения.
   
4. 
   Соединить полученные точки пересечения между собой с учетом видимости линии сечения.
   

Способ нахождения линии пересечения с помощью дополнительных плоскостей называется способом секущих плоскостей, а нахождение линии сечения с помощью дополнительных сфер – способом секущих сфер.

Каким бы способом не производилось нахождение линии пересечения, ее построение начинается с определения характерных точек сечения, а затем определяются промежуточные точки, необходимые для точности построения линии пересечения.

К характерным точкам линии пересечения относятся:

1. 
   точки, проекции которых лежат на проекциях контурных образующих (очерках) заданных поверхностей;
   
2. 
   «крайние» точки – правые и левые, наивысшие и наинизшие, ближайшие и наиболее удаленные.
   

6.8.2.1. Способ секущих плоскостей

Обычно в качестве секущих плоскостей используются плоскости уровня, т.к. линии пересечения их с заданными поверхностями проецируются на плоскость проекций без искажения. Также в некоторых случаях используются и проецирующие плоскости.

Этот способ применяют тогда, когда дополнительные плоскости рассекают заданные поверхности по окружностям-параллелям или прямым-образующим.

Пример: Построить линию пересечения кругового конуса и сферы.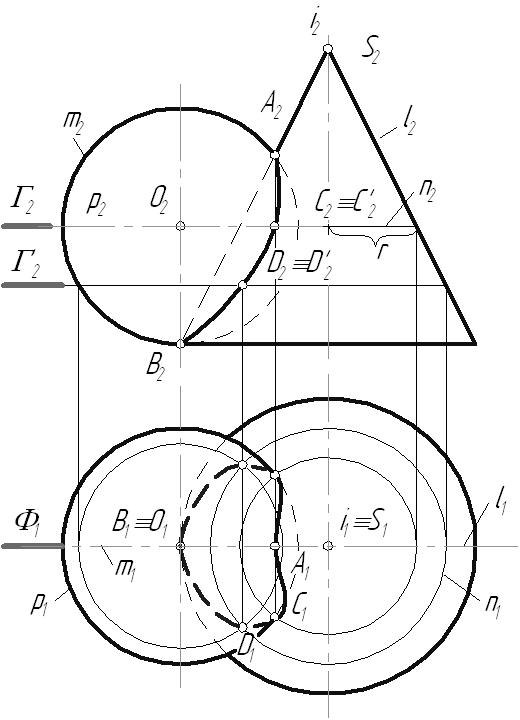



Рис. 6.23

Конус и сфера имеют общую плоскость симметрии , параллельную фронтальной плоскости проекций, с помощью которой находятся высшая и низшая точки линии сечения А и В. Эта плоскость пересекает конус по очерковым образующим l, а сферу – по главному меридиану m.

Обе поверхности содержат семейство параллелей, параллельных горизонтальной плоскости проекций, поэтому остальные точки линии сечения необходимо находить с помощью горизонтальных плоскостей уровня.

ТочкиC и D, лежащие на границе видимости, находятся с помощью плоскости , проходящей через экватор сферы. Эта плоскость, в свою очередь, пересекает конус по параллели n радиуса r.

6.8.2.2. Способ секущих концентрических сфер

Применение сфер в качестве поверхностей-посредников основано на теореме о двух соосных поверхностях вращения.

Следствие этой теоремы:

Сфера, центр которой лежит на оси поверхности вращения, пересекается с последней по окружностям.

Линия пересечения сферы с поверхностью проецируется на одну из плоскостей проекций в виде отрезков, а на другую – в виде окружности.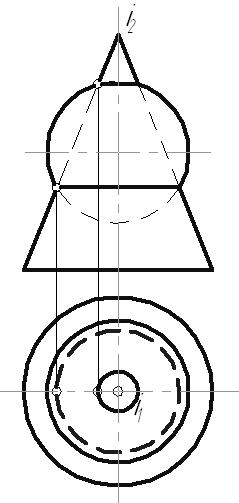

Рис. 6.24.

Этот способ может быть использован лишь при одновременном выполнении трех условий:

1. 
   Пересекающиеся поверхности – поверхности вращения.
   
2. 
   Оси поверхностей пересекаются.
   
3. 
   Поверхности имеют общую плоскость симметрии, параллельную одной из плоскостей проекций.
   

Пример: Построить линию пересечения конуса и цилиндра.

При решении этой задачи сначала строится фронтальная проекция линии пересечения, т.к. общая плоскость симметрии поверхностей параллельна фронтальной плоскости проекций.

«Крайние» точки сечения – высшая и низшая, ближайшая и наиболее удаленная точки (точки, лежащие на границе видимости относительно горизонтальной плоскости проекций) определяются с помощью плоскостей уровня.

Промежуточные точки сечения находятся с помощью секущих сфер, центр которых располагается в точке пересечения осей вращения поверхностей. Сфера минимального радиуса проводится так, чтобы она касалась одной поверхности, а вторую пересекала. Секущие сферы соосны с поверхностями конуса и цилиндра, а следовательно, пересекают их по параллелям.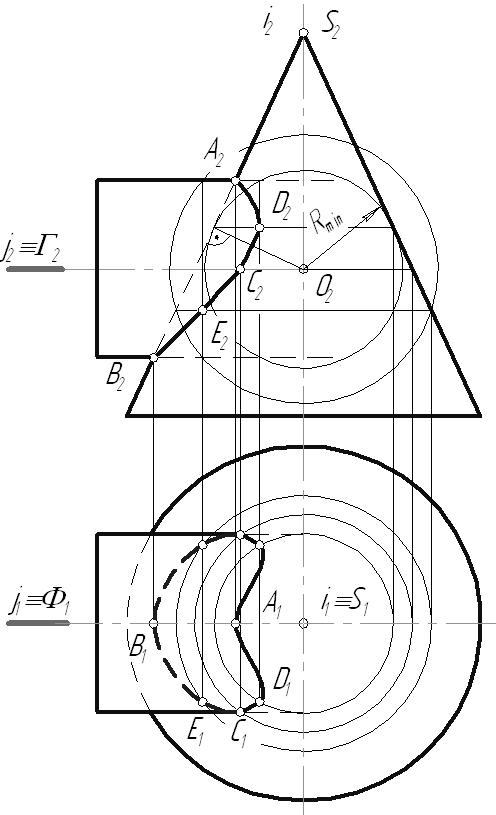



Рис. 6.25

6.8.2.2. Способ секущих эксцентрических сфер

Метод секущих эксцентрических сфер может быть применен при соблюдении следующих условий:

1. 
   Одна из пересекающихся поверхностей циклическая, вторая – поверхность вращения.
   
2. 
   Поверхности должны иметь общую плоскость симметрии, параллельную одной из плоскостей проекций.
   

Сущность метода заключается в следующем: подбирается сфера, пересекающая обе заданные поверхности по окружностям. Точки пересечения этих окружностей будут являться искомыми точками линии сечения.

Пример: Построить линию пересечения закрытого тора с открытым тором.

Заданные поверхности располагаются так, что их оси 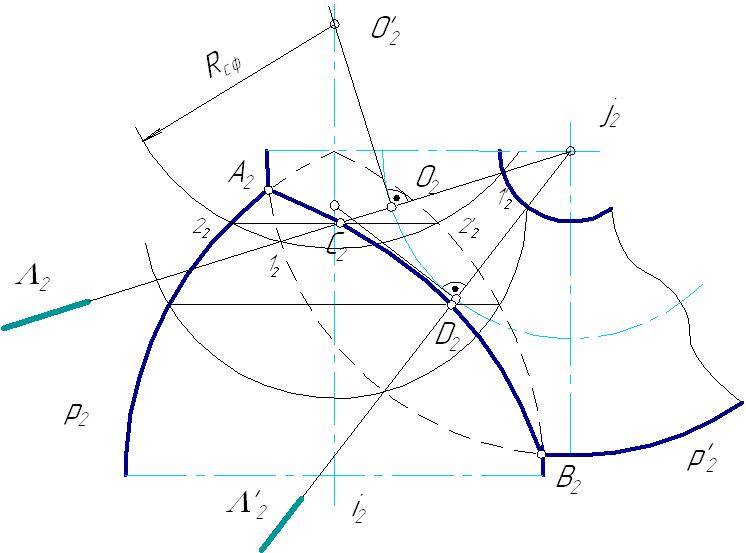, , а фронтальная плоскость является плоскостью симметрии. С помощью этой плоскости находятся высшая и низшая точки сечения.


Рис. 6.26

Для построения промежуточных точек необходимо через ось тора провести фронтально-проецирующую плоскость, пересекающую тор по окружности 1-1.

,

.

О – центр сечения тора, из которого строится перпендикуляр к плоскости . На пересечении этого перпендикуляра с осью второго тора i находится центр первой секущей сферы. Радиус сферы подбирается таким образом, чтобы она пересекла тор по окружности 1-1.



Полученная сфера пересекает тор по параллели 2-2. На пересечении двух окружностей находятся искомые точки С и С.

Остальные точки находятся аналогично.