Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара

• Название: Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара
• Дата: 11.02.2022
• Размер: 5.37 Mb.
• Имя файла: Savchenko_Lektsii_Nachertatelnaya_geometriya.doc
• Тип: Конспект; #358523
• страница: 16 из 20

6.2. Классификация поверхностей

Существует множество различных подходов к классификации поверхностей. Однако главными из них являются следующие критерии:

1. 
   Закон образования поверхности:
   

• 
  поверхности закономерные – если закон их образования известен и может быть выражен математически;
  
• 
  незакономерные.
  

2. 
   Вид образующей:
   

• 
  поверхности линейные – образующая прямая линия;
  
• 
  поверхности нелинейные (криволинейные) – образующая кривая линия.
  

3. 
   Закон движения образующей:
   

• 
  поверхности переноса – с поступательным движением образующей;
  
• 
  поверхности вращения – с вращательным движением образующей;
  
• 
  винтовые поверхности – с винтовым движением образующей.
  

4. 
   Постоянность (вариабильность) формы образующей:
   

• 
  поверхности с образующей постоянной формы;
  
• 
  поверхности с образующей переменной формы.
  

5. 
   Возможность развертывания поверхности:
   

• 
  развертываемые – поверхности, совмещаемые с плоскостью без складок и разрывов:
  
• 
  неразвертываемые.
  

Очевидно, что любую поверхность можно классифицировать одновременно по нескольким признакам. Например, цилиндрическая поверхность вращения:

1. 
   линейчатая закономерная развертываемая поверхность вращения;
   
2. 
   циклическая поверхность переноса окружности постоянного радиуса;
   
3. 
   алгебраическая поверхность второго порядка.
   

Из всего множества поверхностей в кратком курсе начертательной геометрии мы будем рассматривать только гранные поверхности и поверхности вращения.

6.3. Многогранники. Точка и прямая на поверхности

Гранные поверхности имеют прямую образующую и ломаную линию в качестве направляющей.

У пирамидальной поверхности образующая l, двигаясь по ломаной направляющей а, все время проходит через одну точку S, называемую вершиной.

Образующая призматической поверхности, двигаясь в пространстве по ломаной направляющей, все время остается параллельной самой себе.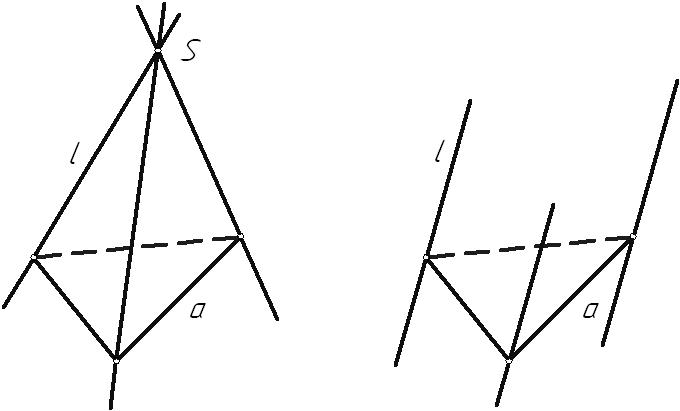



Рис. 6.2

Многогранник – пространственная фигура, ограниченная со всех сторон плоскостями (гранями).

Построение проекций точек, принадлежащих боковой поверхности многогранника, осуществляется с помощью образующих и направляющей.

Возьмем трехгранную пирамиду и точки D,E, F, лежащие на ее боковой поверхности. Необходимо определить недостающие горизонтальные проекции этих точек:

1. 
   Точки E и F лежат на ребрах пирамиды, следовательно, их горизонтальные проекции будут лежать на горизонтальных проекциях соответствующих ребер.
   
2. 
   Точка D принадлежит грани пирамиды, поэтому ее недостающую проекцию следует определять с помощью образующей 1-S. Кроме того, из графического условия не ясно, на какой грани находится точка D, ее фронтальной проекции соответствуют две горизонтальные проекции.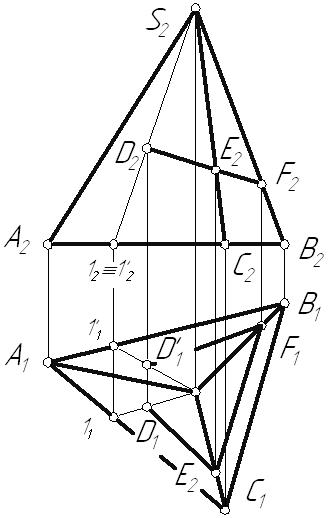
   

Рис. 6.3

Из КЧ видно, что прямая или ломаная линия, принадлежащая поверхности многогранника может быть построена по характерным точкам, которыми являются точки перехода ее через ребра.

6.4. Поверхности вращения

Поверхности вращения имеют произвольную образующую, движущуюся по окружности.

Каждая точка образующей l движется по окружности с центром на оси вращения i(рис. 6.4). Это окружность называется параллелью. Параллель, проходящая через наиболее удаленную от оси вращения точку образующей, называется экватором, а через ближайшую – горлом. Линия m, получаемая при пересечении поверхности плоскостью, проходящей через ось вращения, называется меридианом. Все меридианы поверхности вращения конгруэнтны. Каждый из них разделяется на два, симметричных относительно оси вращения, полумеридиана.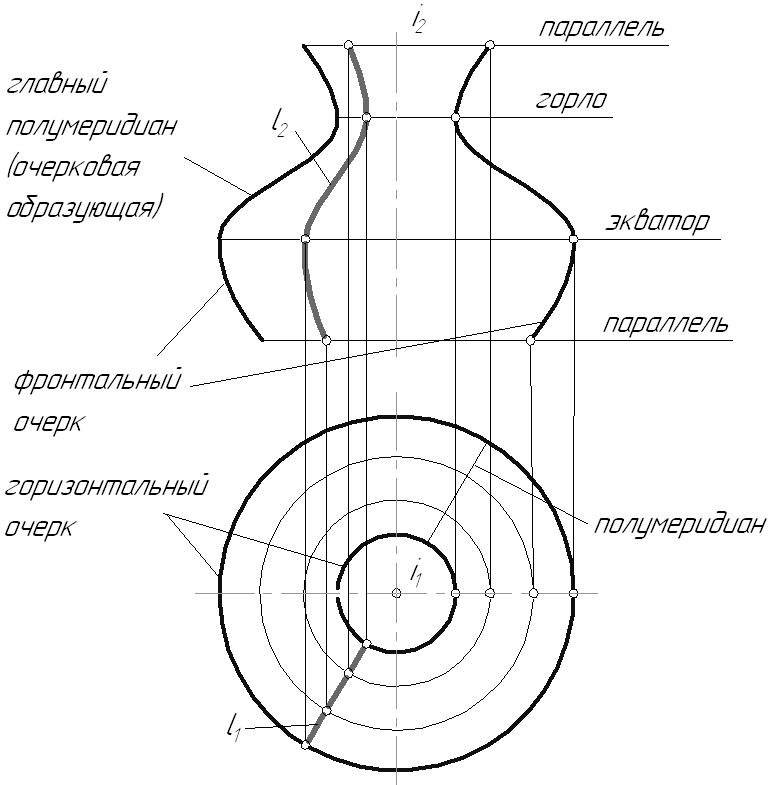



Рис. 6.4

Меридиан, лежащий в плоскости, параллельной плоскости проекций, называется главным меридианом. В данном примере он определяет фронтальный очерк поверхности, горизонтальный очерк определяется экватором и горлом.

6.4.1. Цилиндр вращения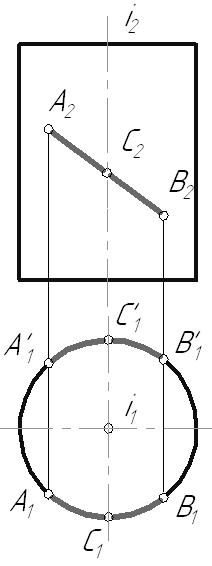

Рис. 6.5
Цилиндрическая поверхность вращения – поверхность, образованная движением прямой линии параллельно оси.

Возьмем фронтально-проеци­рующий цилиндр и линию АВ, расположенную на его боковой поверхности. Горизонтальная проекция этой линии спроецируется на горизонтальный очерк цилиндра, т.к. все ее точки лежат на его боковой поверхности.
Линия принадлежит поверхности, если каждая ее точка принадлежит этой поверхности.

6.4.2. Конус вращения

Коническая поверхность вращения образуется движением прямой линии, пересекающей ось вращения.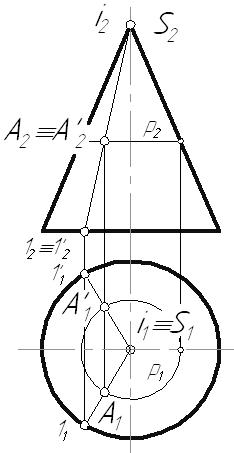

Рис. 6.6

Точка принадлежит поверхности, если она принадлежитлинии, лежащей на этой поверхности.

Построение точек, принадлежащих поверхности вращения, ведется с помощью образующих или параллелей поверхности.

Пусть задана фронтальная проекция точки А, принадлежащей поверхности конуса. Этой проекции соответствуют две горизонтальные проекции точки А₁ и А₁. Их можно определить с помощью образующих поверхности 1-S и 1-S или параллели p.

6.4.3. Однополосный гиперболоид вращения

Гиперболоид вращения – поверхность, образованная вращением прямой вокруг скрещивающейся с ней оси.

Линейчатая поверхность, которую необходимо построить, называется однополосным гиперболоидом вращения. Она образуется вращением прямой l вокруг скрещивающейся с ней оси i. Ближайшая к оси вращения точка образующей описывает наименьшую параллель – горло гиперболоида. Главный меридиан – гипербола.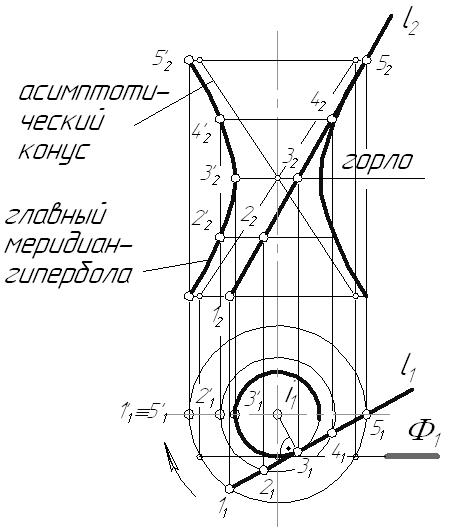

Рис. 6.7
Эта поверхность может быть также получена вращением очерко­вой гиперболы вокруг своей мнимой оси i. Поверхность имеет два семейства прямолинейных образующих, т.к. через одну точку можно провести две прямые – восходящую прямую (как в данной задаче) и нисходящую прямую. Это видно, если касательно к горлу гиперболоида провести плоскость , параллельную оси вращения. Такая плоскость пересекает поверхность по двум прямым. Вторая восходящая прямая образует второе семейство образующих.

Если в центре горла гиперболоида построить конус с таким же углом наклона образующих, как у гиперболоида, то получим так называемый асимптотический конус, к которому поверхность приближается в бесконечности.

6.4.4. Тор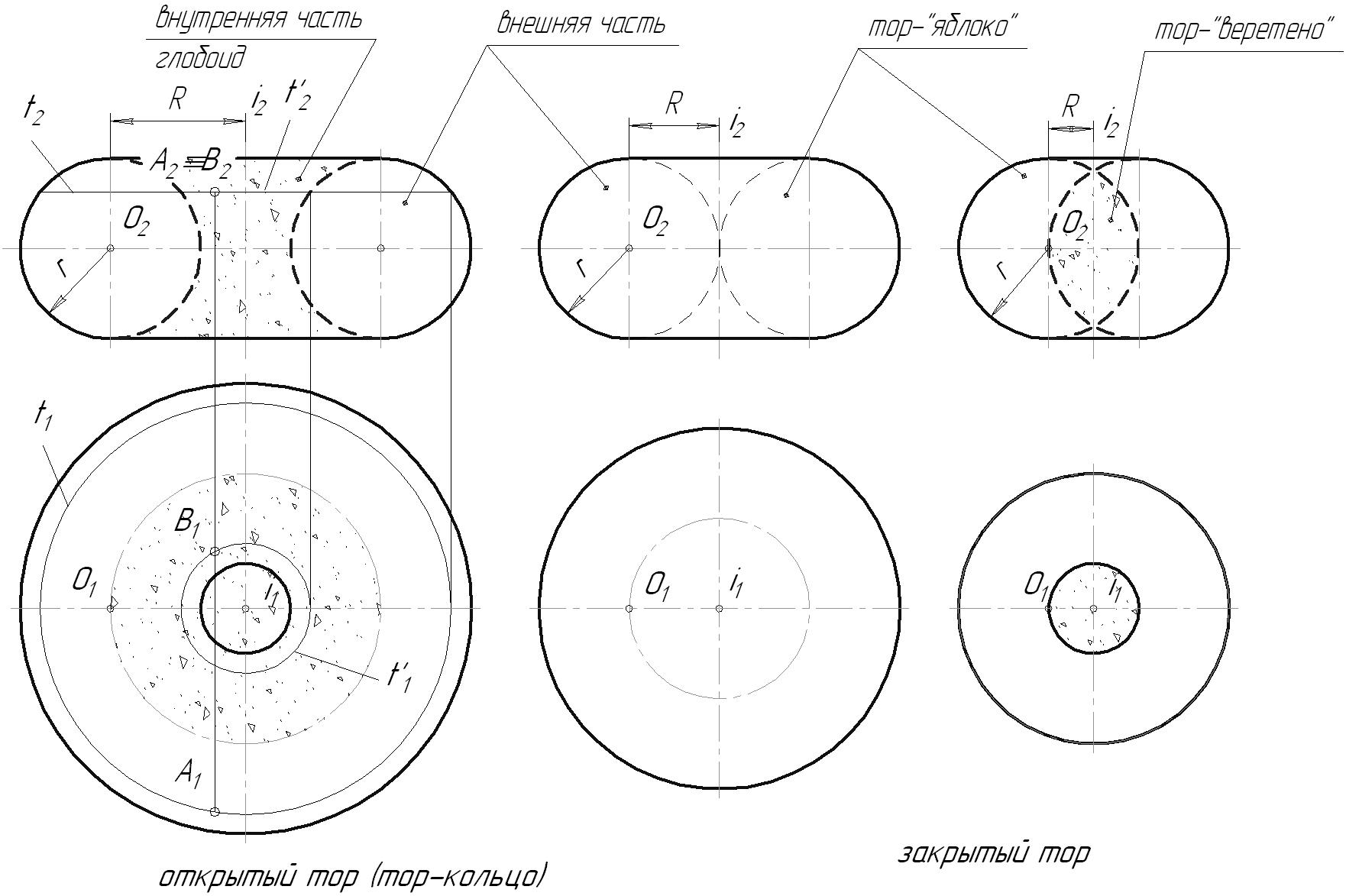

Рис. 6.8

Точка А располагается на параллели внешней части открытого тора, точка В лежит на внутренней параллели. Поверхность тора образуется при вращении окружности вокруг оси, расположенной в плоскости окружности.

В зависимости от соотношения величины радиуса образующей тора r и расстояния от центра окружности до оси вращения t возможны три разновидности тора (рис. 6.8):

• 
  образующая – окружность не пересекает ось вращения ( ) – открытый тор;
  
• 
  образующая – окружность касается оси вращения ( ) – закрытый тор;
  
• 
  образующая – окружность пересекает ось вращения ( ) – закрытый тор.