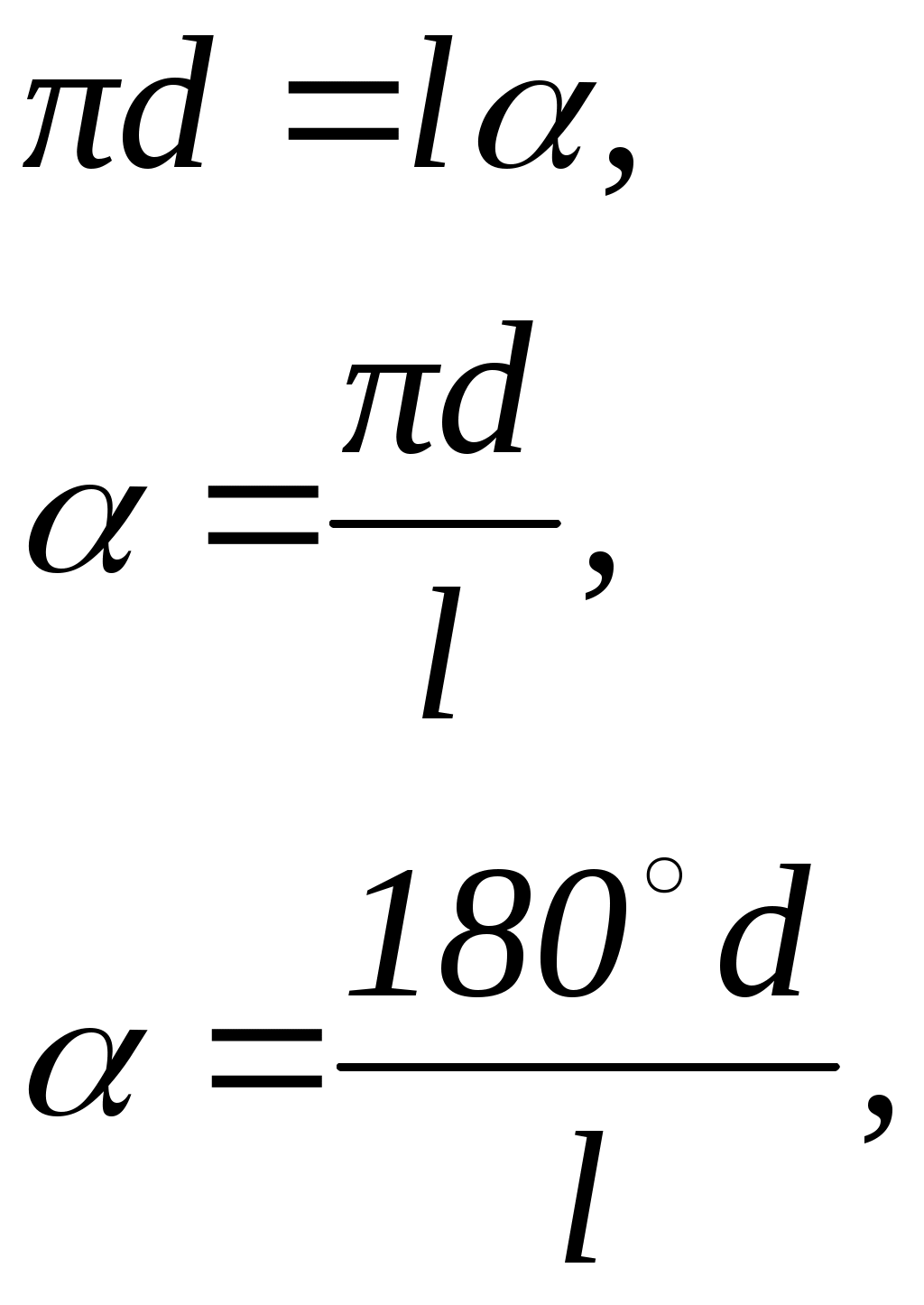Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара

• Название: Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара
• Дата: 11.02.2022
• Размер: 5.37 Mb.
• Имя файла: Savchenko_Lektsii_Nachertatelnaya_geometriya.doc
• Тип: Конспект; #358523
• страница: 18 из 20

Лекция 10

6.7. Пересечение поверхности вращения плоскостью

Форма сечения поверхности вращения плоскостью зависит от угла наклона секущей плоскости к оси вращения поверхности.

Если секущая плоскость:

1. 
   перпендикулярна оси вращения, сечение – окружность;
   
2. 
   наклонена к оси и пересекает все образующие – эллипс;
   
3. 
   параллельна одной образующей – парабола;
   
4. 
   параллельна двум образующим – гипербола;
   
5. 
   проходит через вершину – две пересекающиеся прямые;
   
6. 
   касается поверхности – прямая.
   

Вся совокупность этих линий может быть получена при пересечении конуса плоскостью. Поэтому их называют коническими сечениями, или кониками.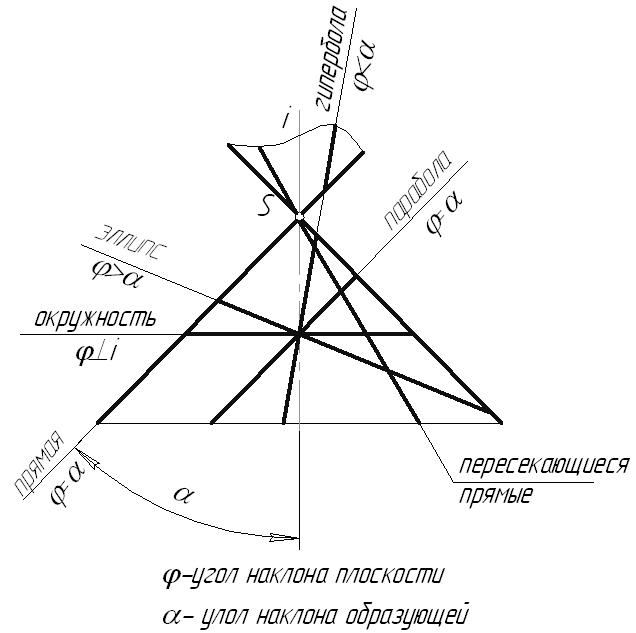



Рис. 6.14

Для построения линии пересечения необходимо найти общие точки поверхности и заданной плоскости. Для определения этих точек необходимо ввести дополнительные секущие плоскости, которые дают наиболее простые линии сечения – окружности или ломаные прямые.

Построение линии сечения начинают с нахождения характерных точек сечения, к которым относятся:

1. 
   высшая и низшая точки;
   
2. 
   крайняя левая и крайняя правая точки, в которых проекции линии сечения касаются очерковых образующих (точки, лежащие на границе видимости);
   
3. 
   ближайшая и наиболее удаленная точки сечения.
   

Пример: Определить линию сечения конуса плоскостью общего положения (hf). Построить развертку нижней отсеченной поверхности конуса.

Анализ формы линии пересечения

Заданная плоскость пересекает только боковую поверхность конуса, следовательно, линией сечения q является эллипс.

Характерные точки линии пересечения:

1. 
   Высшая и низшая точки сечения (А, В) определяют большую ось эллипса и лежат на линии наибольшего наклона плоскости к плоскости основания конуса. Эти точки определяются с помощью дополнительной плоскости .
   

О – центр эллипса

2. 
   Малая ось эллипса (С, D) перпендикулярна к линии наибольшего наклона (большой оси), т.е. лежит на горизонтали плоскости .
   

3. 
   Точки границы видимости (E, F) сечения на лежат в плоскости , делящей конус на видимую и невидимую части по отношению к фронтальной плоскости проекций.
   

Рис. 6.15
Развертка
Полная развертка боковой поверхности конуса представляет собой угол кругового сектора. Ее можно построить двумя способами:

1. 
   Нахождение угла кругового сектора.
   

Рис. 6.16


где d – диаметр окружности основания конуса,

l – длина образующей.

2. 
   Способ малых хорд.
   

Графическое построение величины осуществляется способом малых хорд, при котором окружность основания конуса делится на 8 или 12 равных частей и полученная длина дуги приравнивается ее хорде.

Разрывать отсеченную боковую поверхность следует по наиболее короткой или длинной образующей, так чтобы развертка представляла собой симметричную фигуру и была единым целым.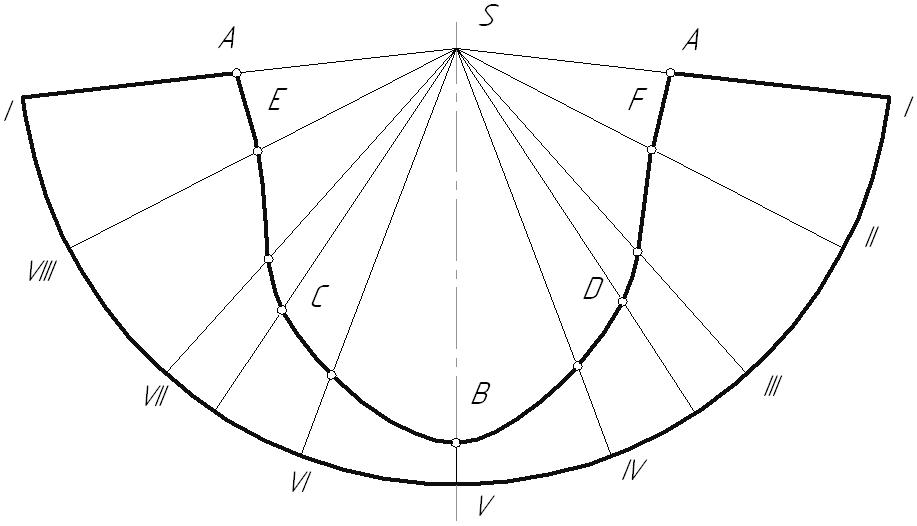



Рис. 6.17