Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара

• Название: Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара
• Дата: 11.02.2022
• Размер: 5.37 Mb.
• Имя файла: Savchenko_Lektsii_Nachertatelnaya_geometriya.doc
• Тип: Конспект; #358523
• страница: 12 из 20

4.3. Перпендикулярность прямой и плоскости

Из курса элементарной геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. Но, исходя из теоремы о проецировании прямого угла, перпендикуляр, проведенный к прямым общего положения, на КЧ проецируется с искажением. Поэтому применительно к начертательной геометрии признак перпендикулярности прямой и плоскости формулируется следующим образом.

Признак перпендикулярности прямой и плоскости:

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся линиям уровня этой плоскости.

Это связано с тем, что только к линиям уровня на плоскостях проекций можно построить прямой угол без искажения. В качестве линий уровня плоскости, при решении задач на перпендикулярность геометрических объектов, обычно выбирают горизонталь и фронталь.

Возьмем плоскость общего положения и проведем в ней горизонталь и фронталь. Затем из точки пересечения линий уровня плоскости восстановим перпендикуляр АК.

На основании теоремы о проецировании прямого угла горизонтальная проекция перпендикуляра к плоскости общего положения на КЧ располагается перпендикулярно горизонтальной проекции горизонтали плоскости, а следовательно, и к ее горизонтальному следу, а фронтальная проекция перпендикуляра – фронтальной проекции фронтали и фронтальному следу.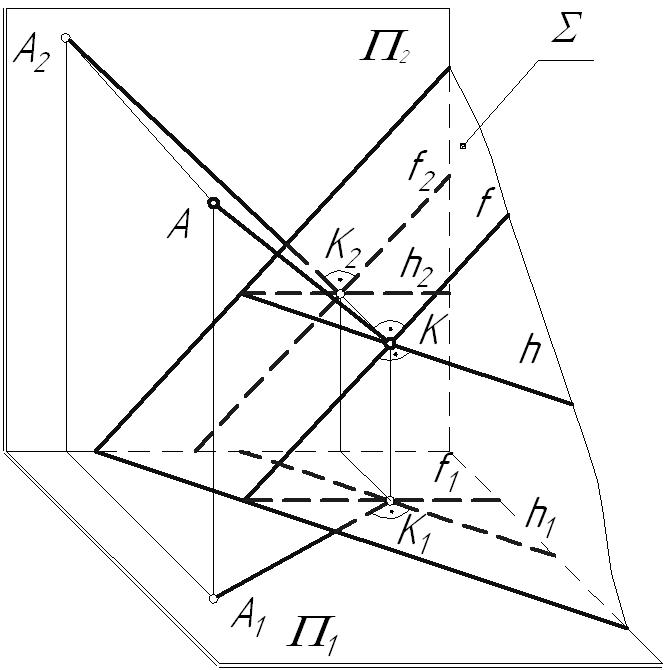



Рис. 4.6

Пример: Из точки А провести перпендикуляр к плоскости 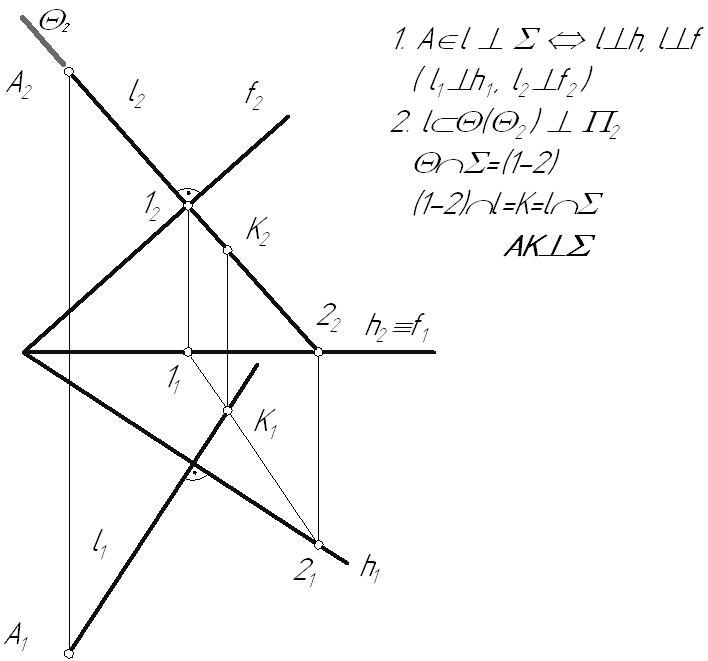и найти его основание.



Рис. 4.7

Частный случай: Прямая перпендикулярна проецирующей плоскости.

В этом случае перпендикулярная прямая будет являться линией уровня и на КЧ перпендикулярными будут вырожденная проекция плоскости (след проекций) и соответствующая проекция прямой.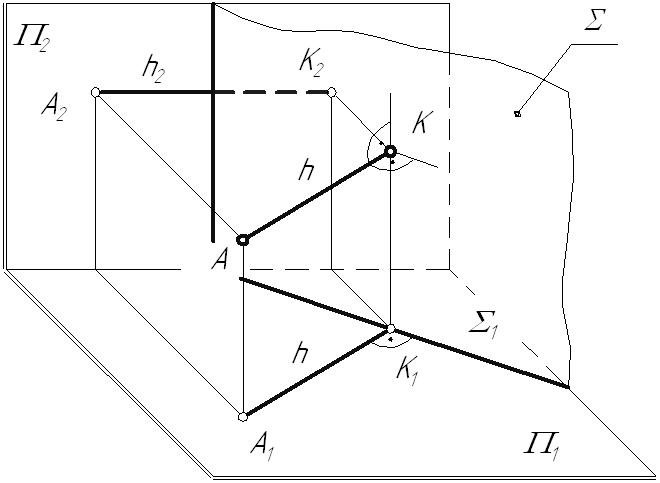



Рис. 4.8

Пример: Найти расстояние от точки А до фронтально-проецирующей плоскости .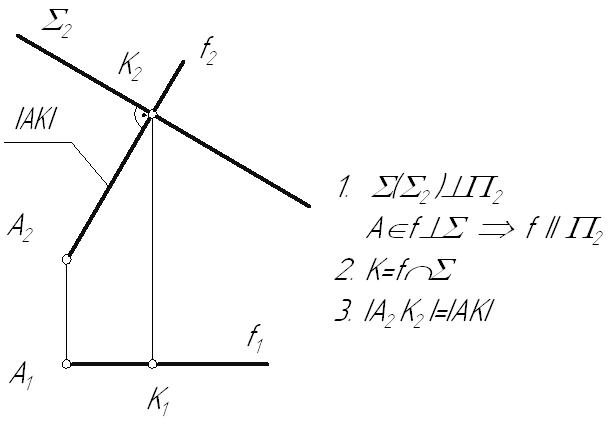



Рис. 4.9

4.4. Перпендикулярность плоскостей

Признак перпендикулярности плоскостей:

Плоскость перпендикулярна другой, если она проходит через перпендикуляр к этой плоскости.

Плоскость перпендикулярна другой плоскости, если она перпендикулярна прямой, лежащей в этой плоскости.

Итак, зная, как располагаются проекции прямой, перпендикулярной плоскости, легко строить взаимно-перпендикулярные плоскости. Исходя из признака перпендикулярности плоскостей можно:

1. 
   построить перпендикуляр к заданной плоскости и через него провести искомую плоскость
   

или

2. 
   в заданной плоскости взять прямую и перпендикулярно ей провести искомую плоскость.
   

В любом из этих случаев задача будет иметь бесчисленное множество решений, если на искомую плоскость не наложены дополнительные условия.

Рассмотрим два примера построения перпендикулярных плоскостей.

Пример: Через точку А провести плоскость, перпендикулярную плоскости .

Вариант 1: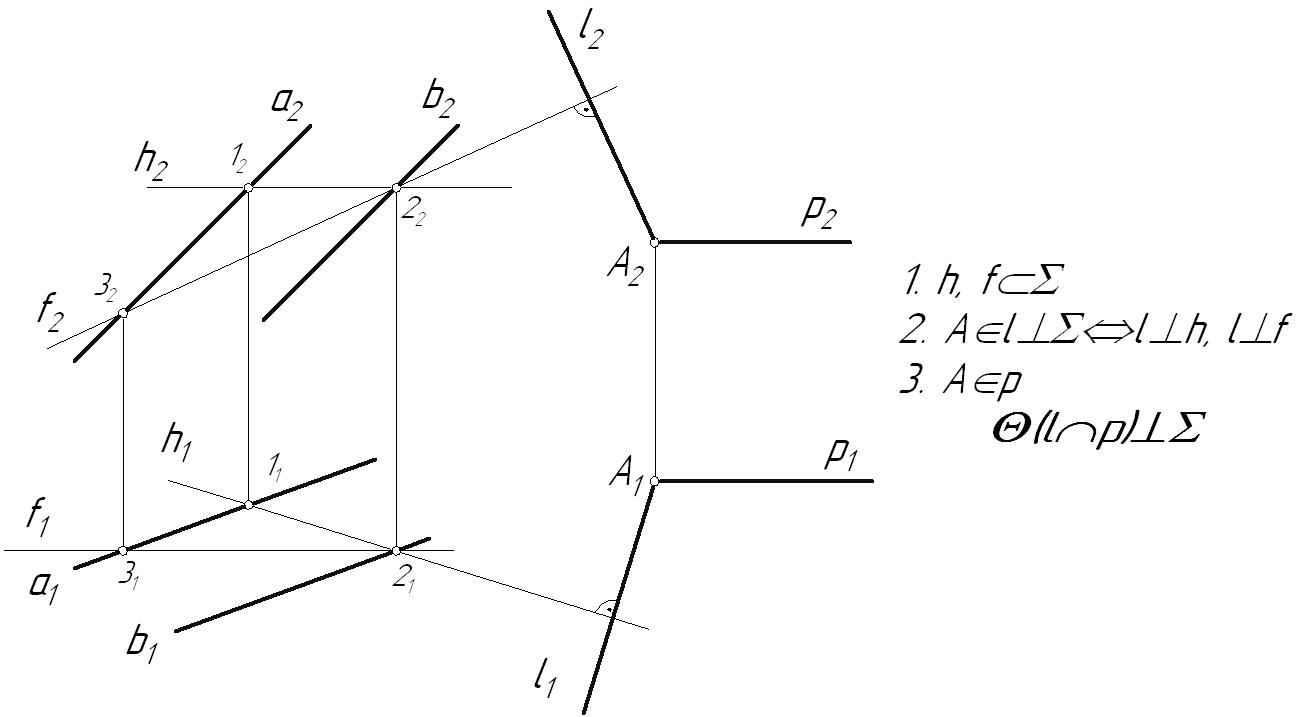



Рис. 4.10

Новая плоскость задана двумя пересекающимися прямыми, одна из которых отвечает условию перпендикулярности плоскостей (прямая l), в зависимости от выбора второй прямой, искомая плоскость может занимать различное положение в пространстве. В данном случае прямая p – профильно-проецирующая, следовательно, сама плоскость является профильно-проецирующей плоскостью.

Вариант 2: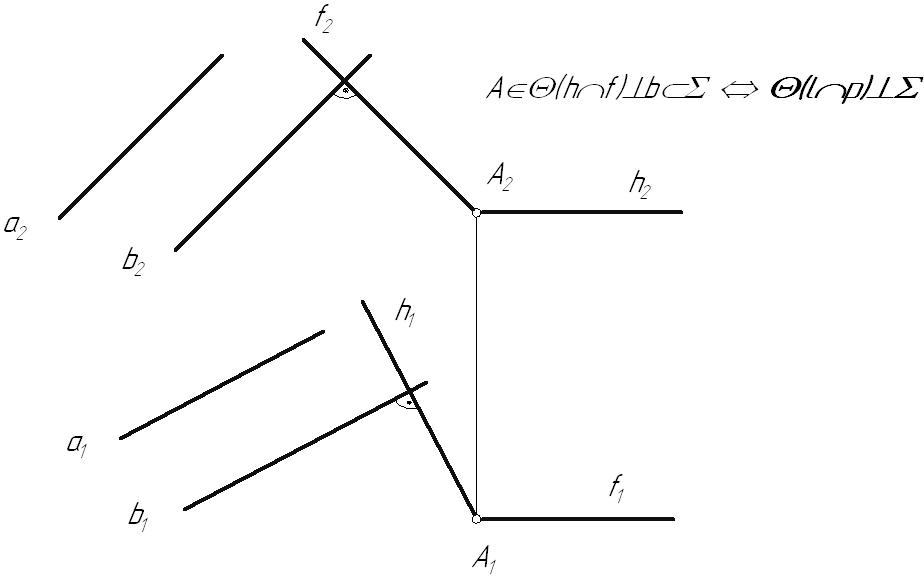



Рис. 4.11