Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара

• Название: Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара
• Дата: 11.02.2022
• Размер: 5.37 Mb.
• Имя файла: Savchenko_Lektsii_Nachertatelnaya_geometriya.doc
• Тип: Конспект; #358523
• страница: 8 из 20

Лекция 3

3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ, ПРЯМЫХ И ПЛОСКОСТЕЙ

3.1. Взаимное расположение точки и прямой

Возможны два варианта расположения точки относительно прямой:

1. 
   точка принадлежит прямой (рис. 3.1 а), тогда, согласно основным свойствам прямоугольного проецирования⁴, на КЧ ее проекции лежат на одноименных проекциях прямой.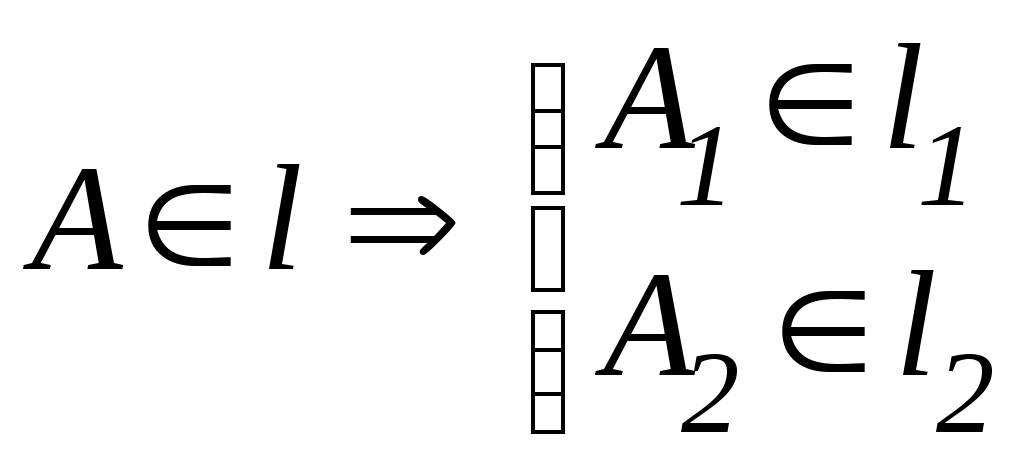
   

;

2. 
   точка не принадлежит прямой (рис. 3.1 б), если хотя бы одна из проекций точки не принадлежит проекции прямой.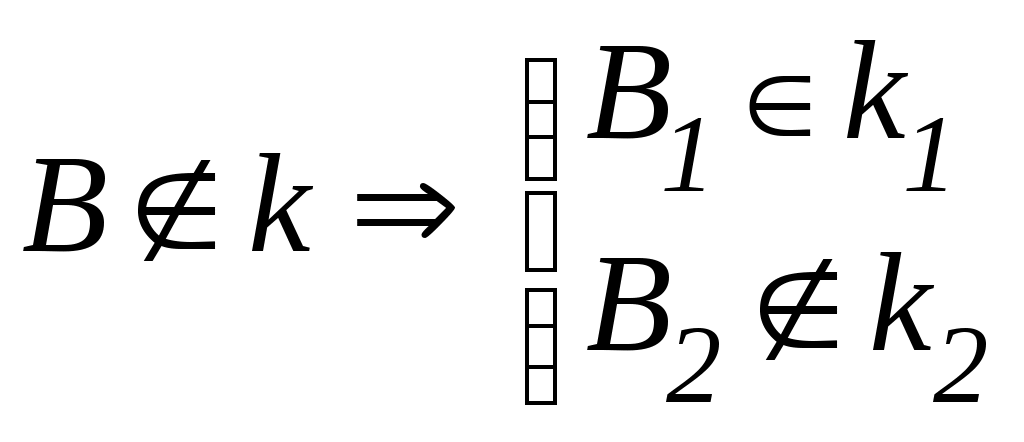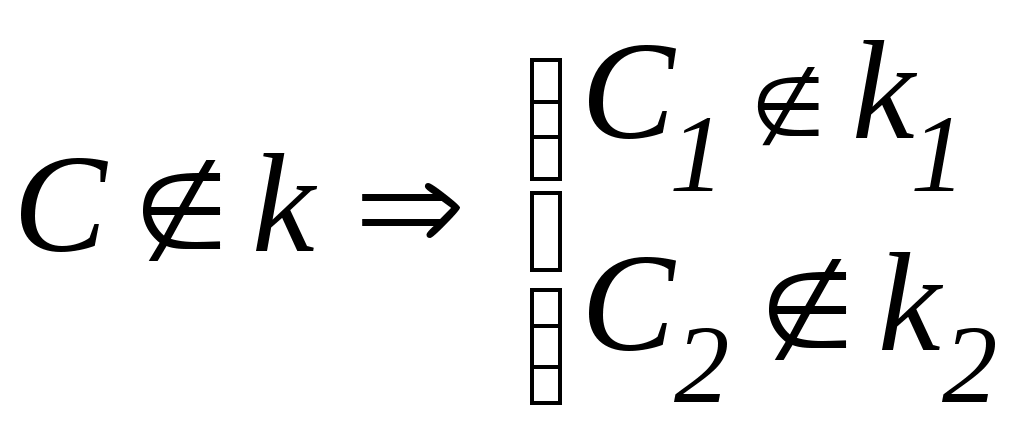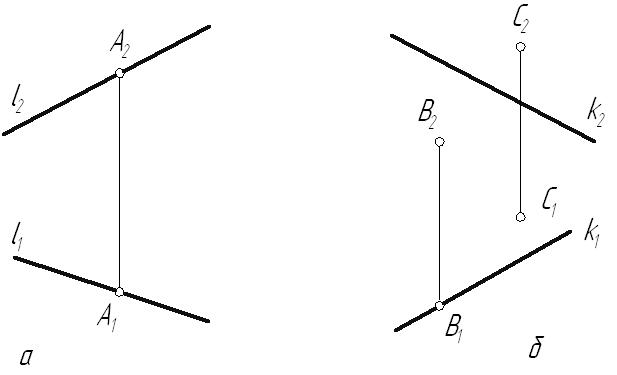
   

; .



Рис. 3.1

3.2. Взаимное расположение прямых

Прямые в пространстве могут занимать относительно друг друга одно из трех положений:

1. 
   быть параллельными;
   
2. 
   пересекаться;
   
3. 
   скрещиваться.
   

Параллельными называются прямые, лежащие в одной плоскости и не имеющие общих точек.

Рис. 3.2

Если прямые параллельны друг другу, то на КЧ их одноименные проекции тоже параллельны (см. п. 1.2).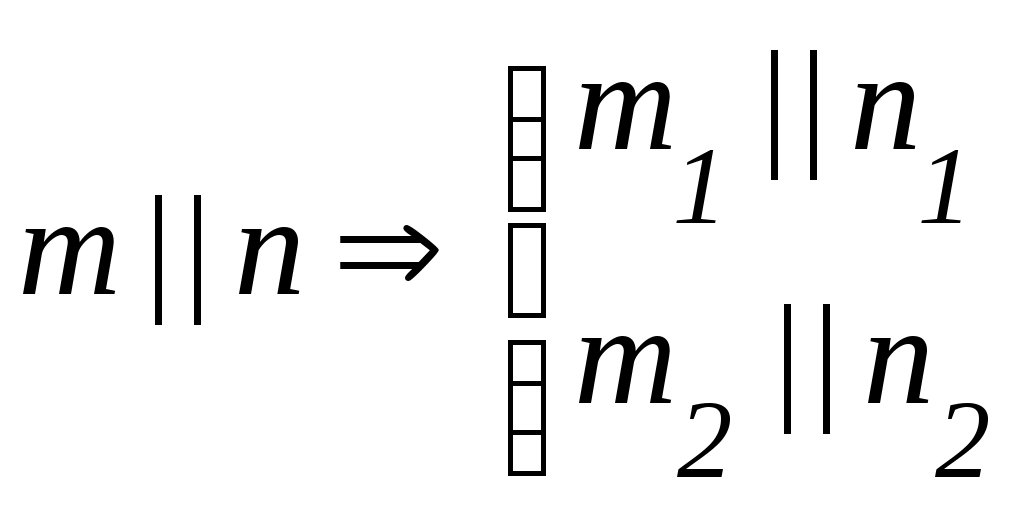

.

Пересекающимися называются прямые, лежащие в одной плоскости и имеющие одну общую точку.

У пересекающихся прямых на КЧ одноименные проекции пересекаются в проекциях точки А. Причем фронтальная ( 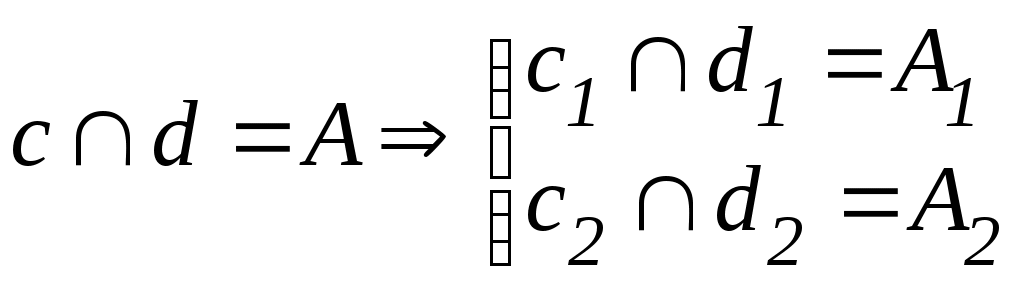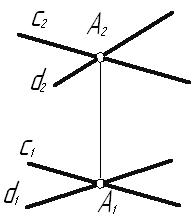) и горизонтальная ( )проекции этой точки должны находиться на одной линии связи.

.



Рис. 3.3

Скрещивающимися называются прямые, лежащие в параллельных плоскостях и не имеющие общих точек.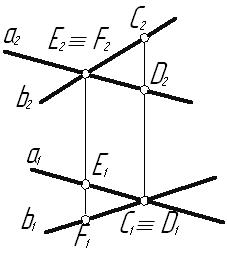

Рис. 3.4

Если прямые скрещивающиеся, то на КЧ их одноименные проекции могут пересекаться, но точки пересечений одноименных проекций не будут лежать на одной линии связи.

На рис. 3.4 точка С принадлежит прямой b, а точка D – прямой а. Эти точки находятся на одинаковом расстоянии от фронтальной плоскости проекций. Аналогично точки E и F принадлежат разным прямым, но находятся на одном расстоянии от горизонтальной плоскости проекций. Поэтому на КЧ их фронтальные проекции совпадают.

3.3. Принадлежность прямой и точки плоскости

Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.5).

Признак принадлежности точки и прямой плоскости:

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.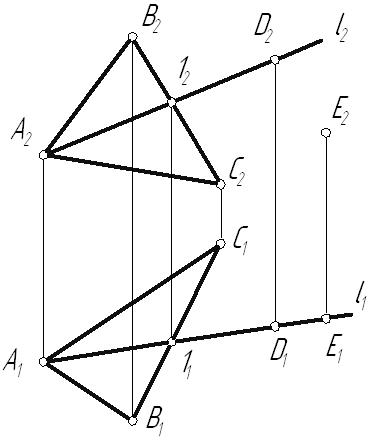

Рис. 3.5

На рис. 3.5 изображена плоскость 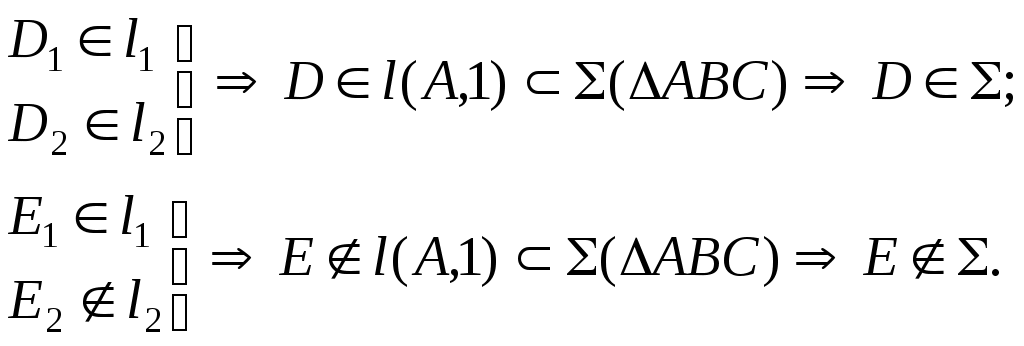и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости.

На рис. 3.6 показана плоскость 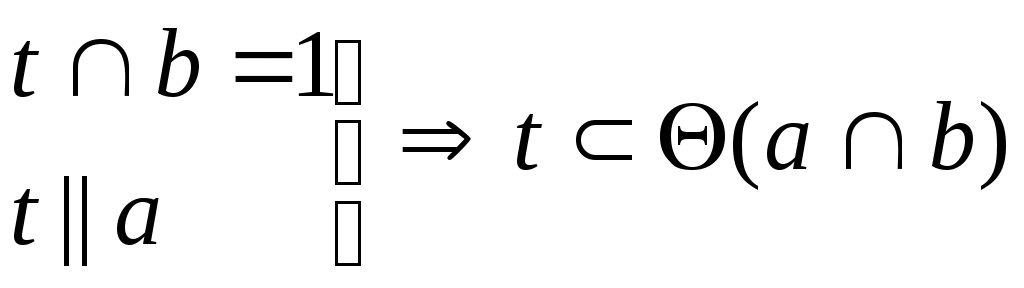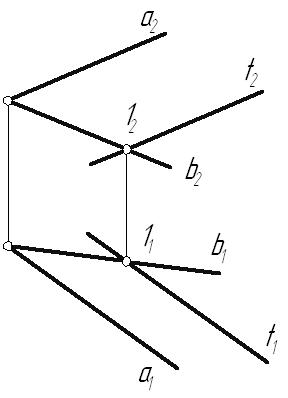и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой а.

.



Рис. 3.6