Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара

• Название: Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара
• Дата: 11.02.2022
• Размер: 5.37 Mb.
• Имя файла: Savchenko_Lektsii_Nachertatelnaya_geometriya.doc
• Тип: Конспект; #358523
• страница: 10 из 20

Лекция 4

3.6. Взаимное расположение прямой и плоскости

Для прямой и плоскости возможны три случая их взаимного расположения:

1. 
   прямая линия может принадлежать плоскости⁵;
   
2. 
   быть параллельна плоскости;
   
3. 
   пересекаться с ней.
   

3.6.1. Параллельность прямой и плоскости

Признак параллельности прямой и плоскости хорошо известен из курса стереометрии:

Прямая параллельна плоскости, если она параллельна прямой, принадлежащей этой плоскости.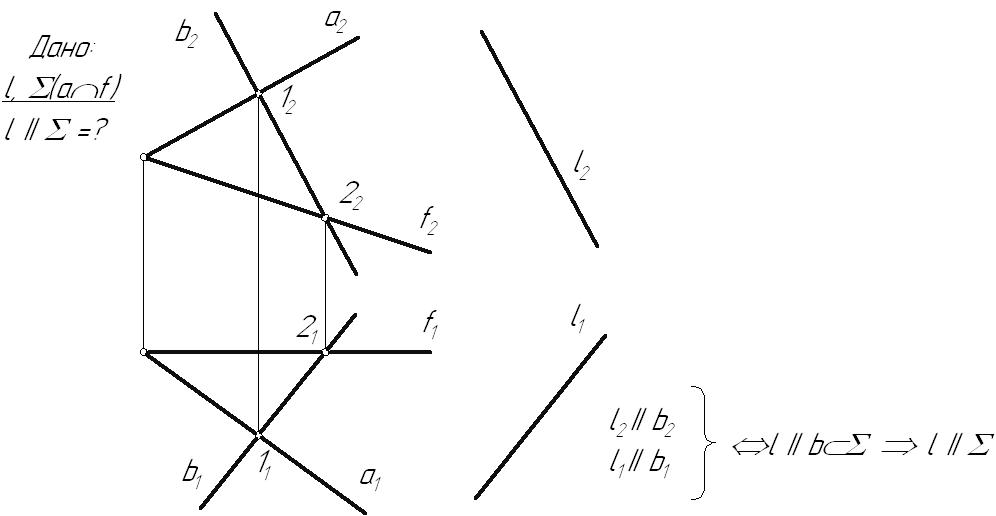



Рис. 3.16

3.6.2. Определение видимости на КЧ

Для улучшения наглядности изображений, заданных на КЧ, принято видимые для наблюдателя линии показывать сплошными, а невидимые – штриховыми линиями. При этом предполагается, что:

1. 
   плоскости и поверхности непрозрачны;
   
2. 
   луч зрения от наблюдателя всегда попадает перпендикулярно к той плоскости проекций, относительно которой определяется видимость.
   

На рисунке 3.17 заданы две пары точек:

1. 
   точки А и В, находящиеся на одном проецирующем луче, направленном перпендикулярно горизонтальной плоскости проекций ;
   
2. 
   точки С и D, через которые проходит проецирующий луч, перпендикулярный фронтальной плоскости проекций .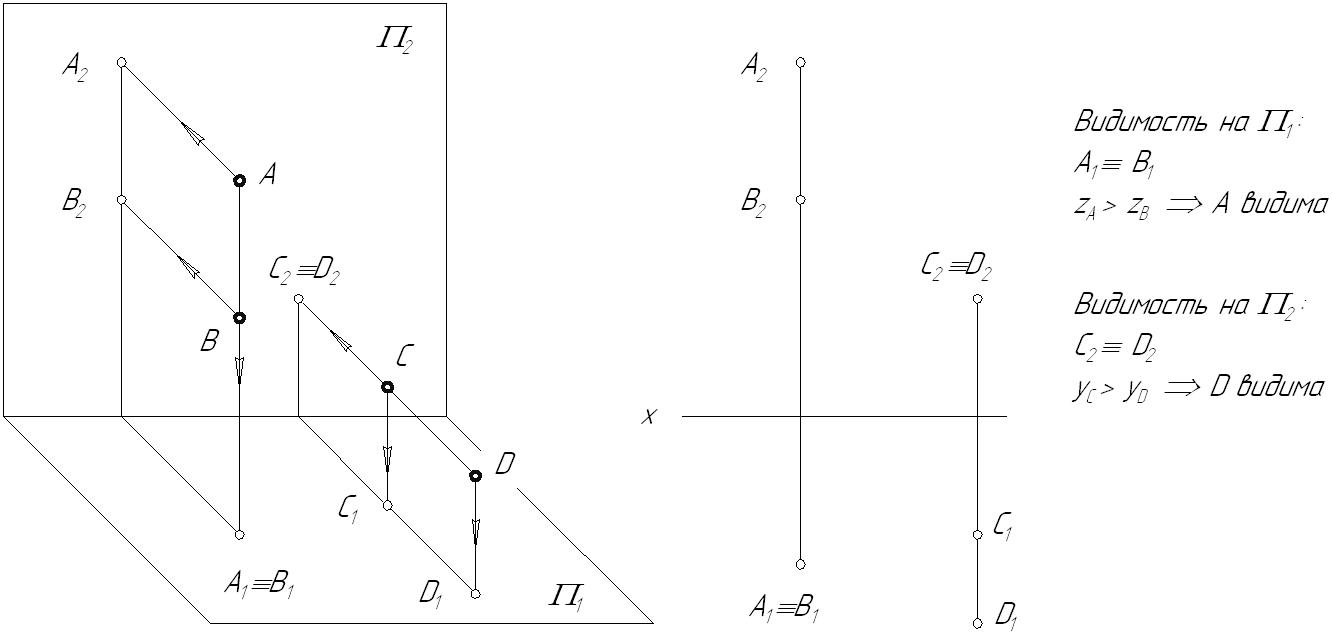
   

Рис. 3.17

Необходимо определить видимость точек относительно горизонтальной и фронтальной плоскостей проекций.

Если на КЧ какие-либо две проекции точек совпадают, то для наблюдателя будет видима та точка, проекция которой находится дальше от оси проекций.

Точки А и В, С и D называются точками, конкурирующими в видимости, а сам метод определения видимости – методом конкурирующих точек.

Конкурирующими в видимости точками называются точки, лежащие на одном проецирующем луче, но принадлежащие разным геометрическим объектам.

3.6.3. Пересечение прямой с плоскостью

Прямая называется пересекающей плоскость, если она имеет с ней только одну общую точку. Рассмотрим различные случаи пересечения прямой и плоскости.

Частные случаи:

Пример 1. Прямая – проецирующая, плоскость – частного положения.

На КЧ необходимо построить проекции точки пересечения прямой с плоскостью и определить видимость этой прямой относительно горизонтальной и фронтальной плоскостей проекций.

Точка К должна одновременно принадлежать и прямой, и плоскости.

1. 
   Горизонтальную проекцию точки пересечения находим из условия принадлежности ее прямой i. Так как все точки, лежащие на горизонтально-проецирующей прямой, совпадают с ее следом: К₁ i₁.
   

2. 
   Определение фронтальной проекции точки пересечения сводится к задаче на принадлежность точки К плоскости :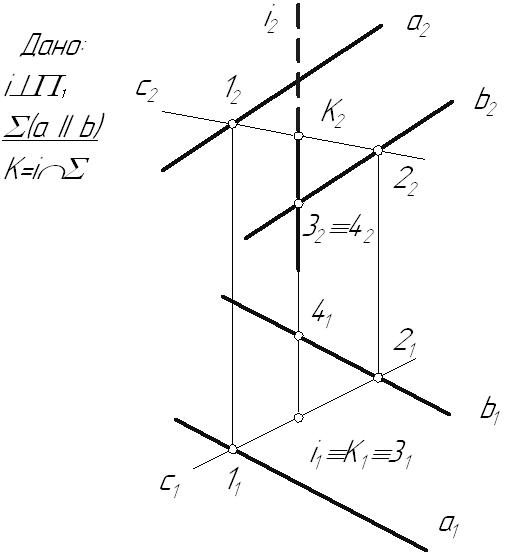
   

.



Рис. 3.18

Пример 2. Прямая – общего положения, плоскость – проецирующая.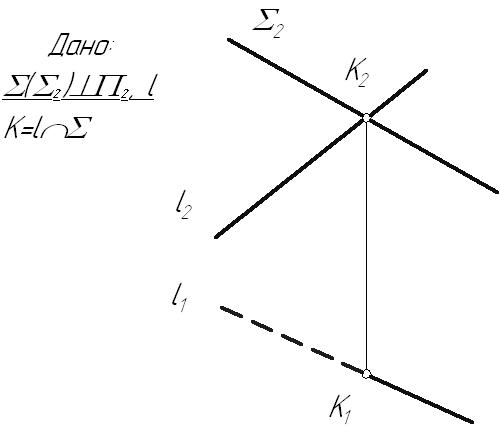

Рис. 3.19
В данном случае фронтальная проекция точки пересечения лежит на следе плоскости

.

Построение недостающей горизонтальной проекции точки пересечения сводится к задаче на принадлежность точки прямой:

.

Общий случай:

Пересечение прямой общего положения с плоскостью общего положения (первая основная позиционная задача).

В общем случае задача на пересечение прямой с плоскостью решается с помощью вспомогательной секущей плоскости, на которую накладывается ряд условий:

1. 
   она должна быть плоскостью частного положения;
   
2. 
   должна проходить через заданную прямую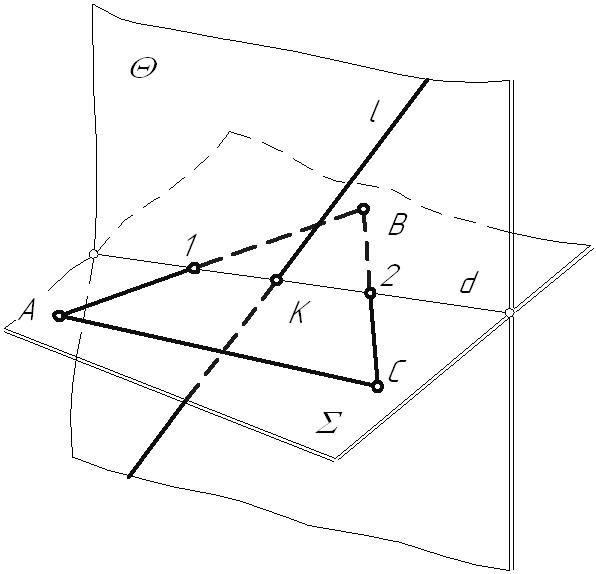
   

Рис. 3.20

Порядок нахождения точки пересечения прямой с плоскостью:

1. 
   Через прямую l проводится вспомогательная плоскость частного положения .
   
2. 
   Определяется линия пересечения вспомогательной плоскости с заданной плоскостью .
   
3. 
   На пересечении линии пересечения плоскостей 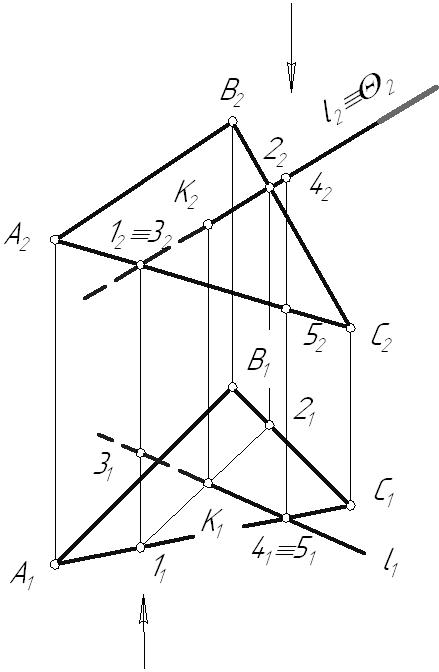с заданной прямой находится точка К, являющаяся искомой точкой.
   

Рис. 3.21