Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара

• Название: Конспект лекций Утверждено Редакционноиздательским советом университета в качестве учебного пособия Самара
• Дата: 11.02.2022
• Размер: 5.37 Mb.
• Имя файла: Savchenko_Lektsii_Nachertatelnaya_geometriya.doc
• Тип: Конспект; #358523
• страница: 20 из 20

Лекция 12

7. АКСОНОМЕТРИЧЕСКИЕ ИЗОБРАЖЕНИЯ

При разработке проектно-конструкторской документации, наряду с ортогональными проекциями, применяются аксонометрические. Эти изображения, с одной стороны, пространственно наглядны, с другой – дают возможность измерений.

Сущность аксонометрического проецирования заключается в том, что геометрический объект, ориентированный определенным образом относительно ортогональной системы плоскостей проекций, проецируется вместе с осями проекций на новую плоскость, называемую аксонометрической или картинной. В результате этого проецирования получается одна аксонометрическая проекция (аксонометрия).

7.1. Принцип аксонометрического проецирования

Возьмем в пространстве прямоугольную систему координат 0xyz и точку А, связанную с этой системой. Спроецируем эту точку по направлению S на картинную плоскость .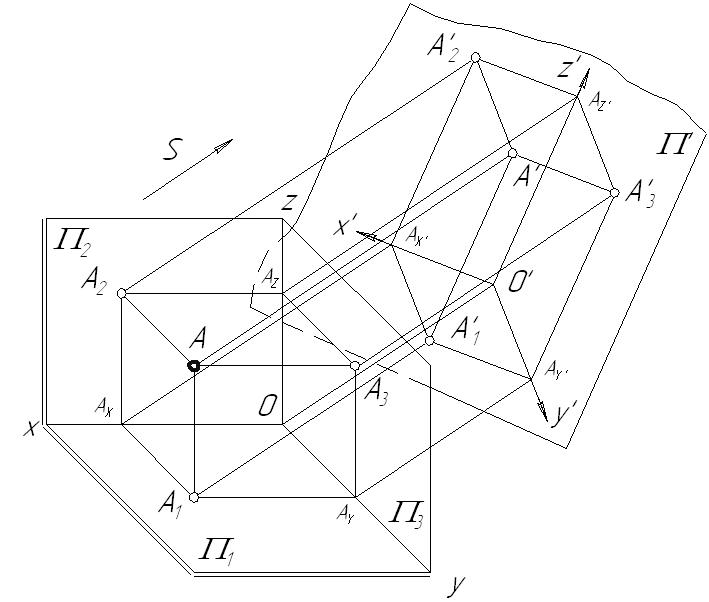

Рис. 7.1

аксонометрические оси

При проецировании на картинную плоскость происходит искажение отрезков, параллельных осям проекций. Мерой этого искажения являются коэффициенты искажения – отношение длины отрезка, параллельного аксонометрическим осям, к его натуральной величине.

– коэффициент искажения по оси 0’x’;

– коэффициент искажения по оси 0’y’;

– коэффициент искажения по оси 0’z’.

7.2. Виды аксонометрических проекций

В зависимости от направления проецирования (S) аксонометрические проекции подразделяются на:

1. 
   прямоугольные ;
   
2. 
   косоугольные (S  ).
   

Каждый из этих видов проекций делится на три вида:

1. 
   Изометрия – коэффициенты искажений по всем осям одинаковы.
   

2. 
   Диметрия – коэффициенты искажений по двум осям одинаковы.
   

– горизонтальная диметрия

– фронтальная диметрия

– профильная диметрия

3. 
   Триметрия – коэффициенты искажений по трем осям различны.
   

.

Стандартными аксонометрическими изображениями являются прямоугольные изометрия и диметрия, а также косоугольные фронтальная и горизонтальная изометрии и фронтальная диметрия (ГОСТ 2.317-69).

7.3. Связь между коэффициентами искажений

Теорема:

Сумма квадратов коэффициентов искажений есть величина постоянная и не зависящая от положения ортогональных плоскостей проекций.

.

Пусть две ортогональные оси проекций совпадают с аксонометрической плоскостью. Спроецируем третью ось на эту плоскость по направлению S.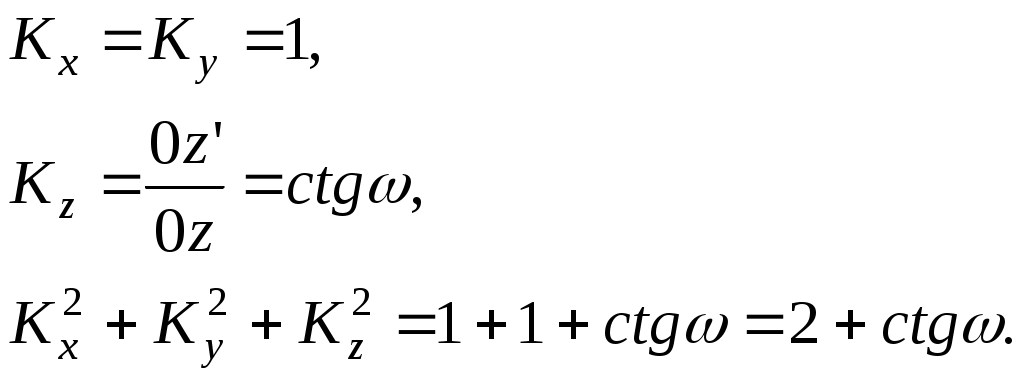

где  – угол между направлением проецирования и картинной плоскостью.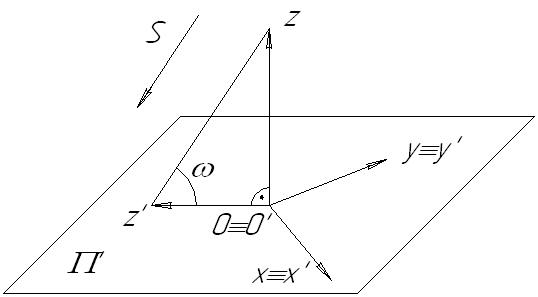



Рис. 7.2

7.4. Коэффициенты искажений прямоугольной аксонометрии

При , тогда

.

Коэффициенты изменяются в диапазоне .

– аксонометрическая плоскость перпендикулярна какой-либо оси.

– аксонометрическая плоскость параллельна какой-либо оси, тогда аксонометрическая проекция превращается в ортогональную.

Аксонометрические проекции не могут быть взяты параллельно или перпендикулярно осям проекций, а картинная плоскость должна пересекать все три плоскости проекций.

Прямоугольная изометрия

В изометрии , тогда уравнение связи коэффициентов имеет вид .
Таким образом, в прямоугольной изометрической проекции коэффициенты искажения по всем трем осям равны

.

Прямоугольная фронтальная диметрия

В стандартной диметрии принимают , а .

, , .

Следовательно, в прямоугольной фронтальной диметрии коэффициенты искажения по осям равны:

Kx0,94, Kz0,94, Ky0,47.

7.5. Приведенные коэффициенты искажения

На практике, в целях сокращения вычислений, рекомендуется пользоваться приведенными коэффициентами искажений. При этом изображение строиться в масштабе , где коэффициент m называется коэффициентом приведения, а аксонометрия называется практической или приведенной.

Прямоугольная изометрия

,

.

Следовательно, в приведенной изометрии изображение увеличено в 1,22 раза.

Оси изометрической проекции располагаются под углом 120 друг к другу.

Прямоугольная фронтальная диметрия

,

,

.

Косоугольная фронтальная диметрия

В косоугольной фронтальной диметрии (кабинетная проекция) картинная плоскость располагается параллельно фронтальной плоскости x0z, а направление проецирования выбирают так, что коэффициент искажения по оси 0y равен 0,5. Поэтому в косоугольной аксонометрии нет необходимости использовать приведенные коэффициенты искажения.

7.6. Углы между аксонометрическими осями. Построение аксонометрических проекций геометрических элементов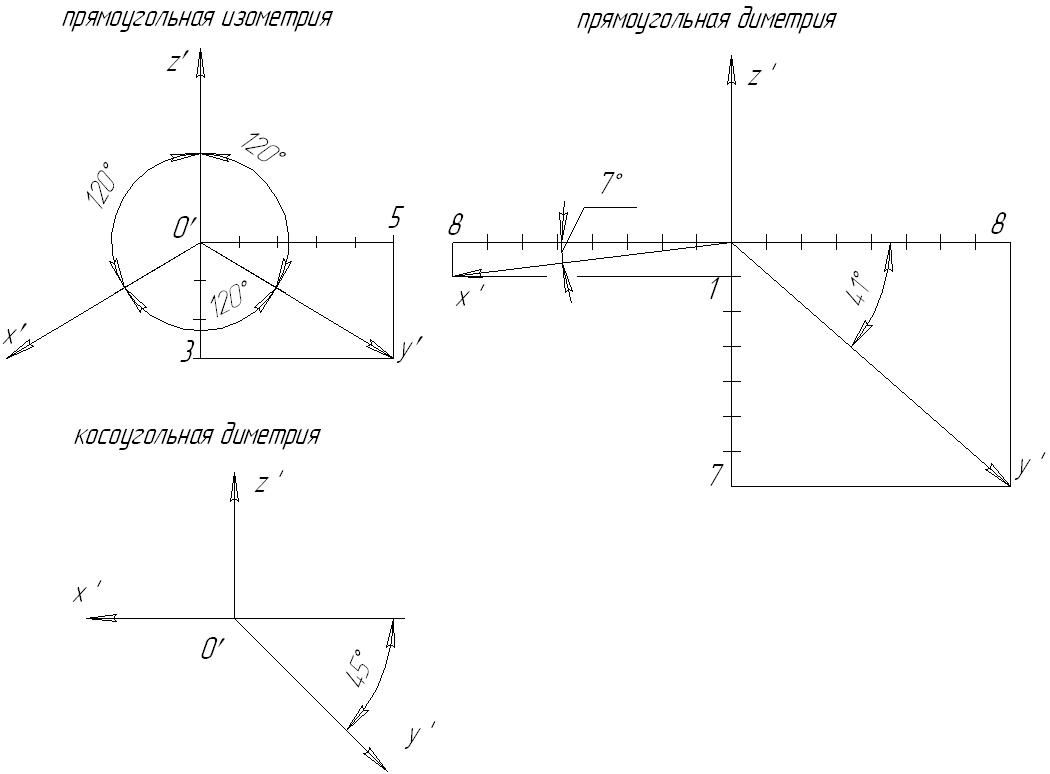

Рис. 7.3

Для построения аксонометрической проекции точки при заданном направлении аксонометрических осей необходимо отложить на них действительные координаты этой точки с учетом коэффициентов искажений: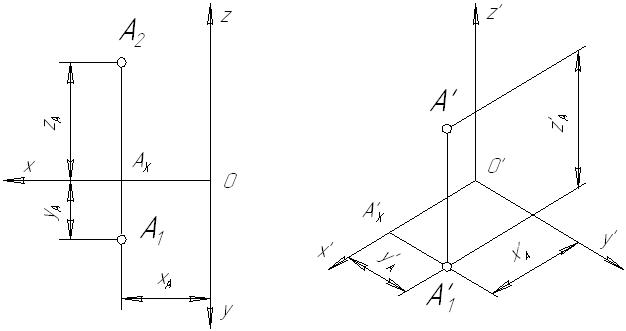

, , .



Рис. 7.4

Рассмотрим построение аксонометрических изображений окружностей, расположенных в плоскостях проекций.

Если в плоскости проекций или параллельной ей плоскости располагается окружность, то на картинную плоскость она спроецируется ортогонально в виде эллипса.

Проекцией окружности, параллельной плоскости проекций, в ортогональной аксонометрии является эллипс, большая ось которого перпендикулярна «свободной» аксонометрической оси, а малая – совпадает с этой осью.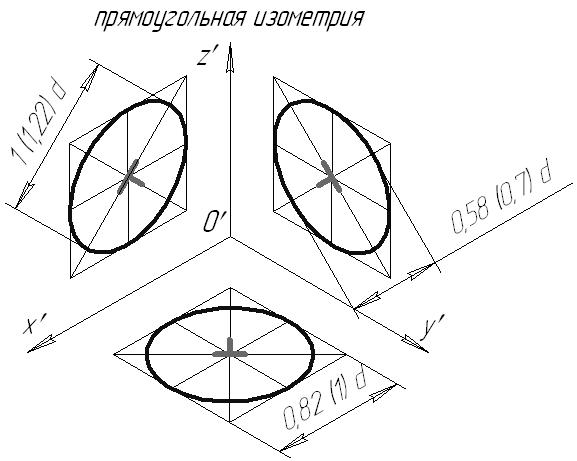



Рис. 7.5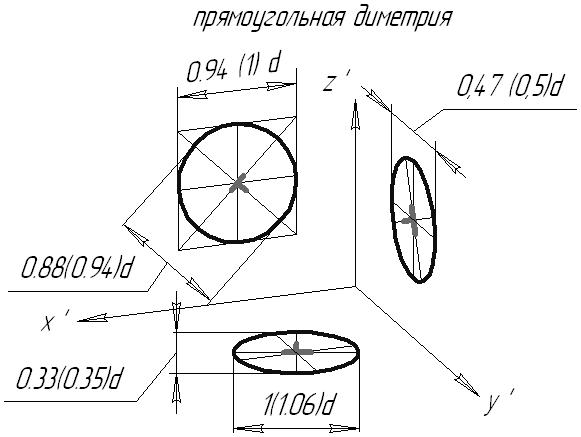

Рис. 7.6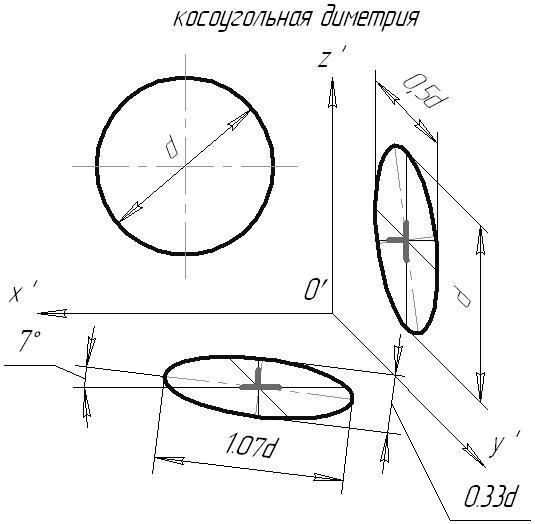



Рис. 7.7

На рисунках 7.8 и 7.9 приведены примеры построения практической прямоугольной изометрии и практической прямоугольной и косоугольной диметрии цилиндрической детали с прямоугольным вырезом.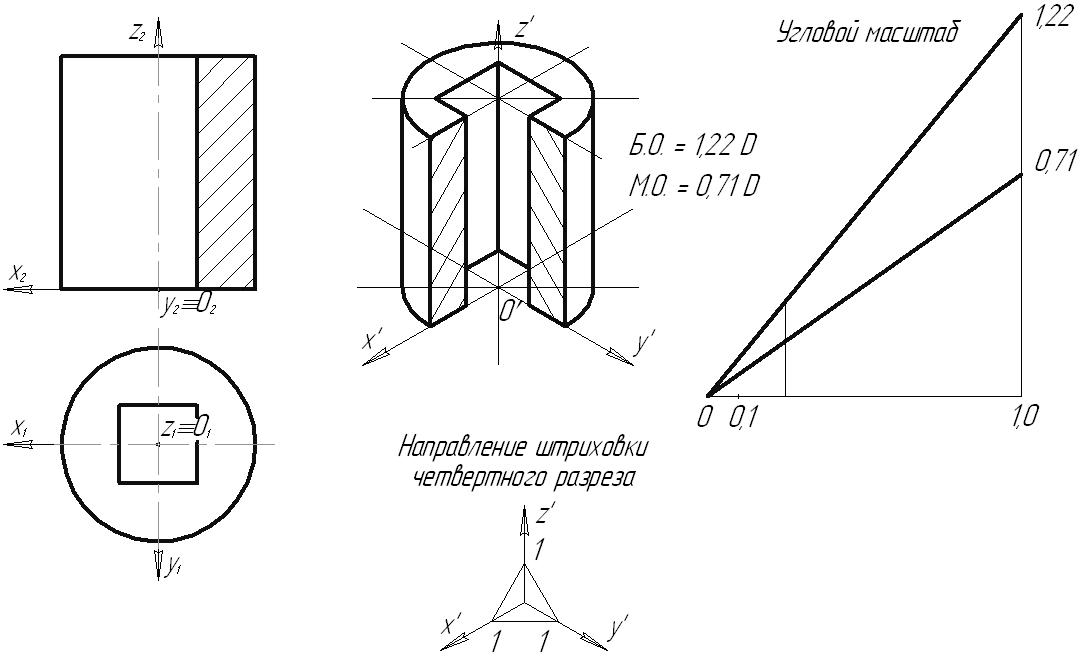



Рис. 7.8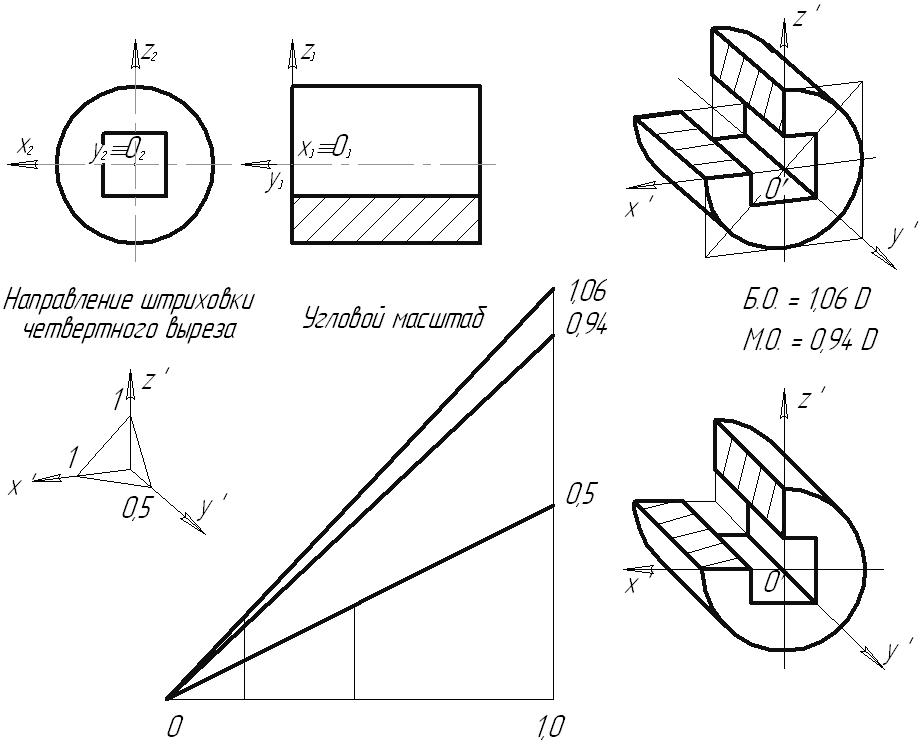



Рис. 7.9

Содержание

Введение 4

Условные обозначения геометрических объектов 5

Символы взаиморасположения геометрических объектов и логических операций 6

Греческий алфавит 7

Список рекомендуемой литературы 8

Лекция 1 9

1. ОСНОВЫ ТЕОРИИ ПОСТРОЕНИЯ ЧЕРТЕЖА 9

1.1. Виды проецирования 9

1.2. Основные свойства параллельного проецирования 10

2. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ 13

2.1. Комплексный чертеж точки (Эпюр Монжа) 13

Лекция 2 16

2.2. Проецирование прямой 16

2.2.1. Положение прямой относительно плоскостей проекций 17

2.2.2. Следы прямых линий 21

2.2.3. Деление отрезка в заданном отношении 22

2.2.4. Натуральная величина отрезка прямой общего положения. Метод прямоугольного треугольника 26

2.3. Плоскость. Способы ее задания, положение относительно плоскостей проекций 30

Лекция 3 35

3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ, ПРЯМЫХ И ПЛОСКОСТЕЙ 35

3.1. Взаимное расположение точки и прямой 35

3.2. Взаимное расположение прямых 36

3.3. Принадлежность прямой и точки плоскости 39

3.4. Линии уровня плоскости 41

3.5. Взаимное расположение плоскостей 43

Лекция 4 50

3.6. Взаимное расположение прямой и плоскости 50

3.6.1. Параллельность прямой и плоскости 50

3.6.2. Определение видимости на КЧ 50

3.6.3. Пересечение прямой с плоскостью 51

Лекция 5 55

4. ПЕРПЕНДИКУЛЯРНОСТЬ ГЕОМЕТРИЧЕКСКИХ ОБЪЕКТОВ 55

4.1. Проецирование прямого угла 55

4.2. Линия наибольшего наклона плоскости 56

4.3. Перпендикулярность прямой и плоскости 57

4.4. Перпендикулярность плоскостей 61

4.5. Перпендикулярность прямых общего положения 63

Лекция 6 64

5. ПРЕОБРАЗОВАНИЕ ИЗОБРАЖЕНИЙ. ЧЕТЫРЕ ОСНОВНЫЕ ЗАДАЧИ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ 64

5.1. Метод замены плоскостей проекций 64

5.2. Вращение вокруг линии уровня 65

Лекция 7 67

5.3. Вращение вокруг проецирующих прямых 67

5.3.1. Вращение точки 68

5.3.2. Вращение прямой 68

5.3.3. Вращение плоскости 69

5.4. Плоскопараллельное перемещение 70

Лекция 8 71

6. ПОВЕРХНОСТИ 71

6.1. Способы задания поверхности 71

6.2. Классификация поверхностей 73

6.3. Многогранники. Точка и прямая на поверхности 74

6.4. Поверхности вращения 76

6.4.1. Цилиндр вращения 77

6.4.2. Конус вращения 77

6.4.3. Однополосный гиперболоид вращения 78

6.4.4. Тор 79

Лекция 9 79

6.5. Пересечение поверхности многогранника плоскостью 79

6.6. Пересечение прямой с поверхностью 82

Лекция 10 84

6.7. Пересечение поверхности вращения плоскостью 84

6.8. Пересечение поверхностей 89

6.8.1. Пересечение многогранников 89

Лекция 11 90

6.8.2. Пересечение поверхностей вращения 90

Лекция 12 97

7. АКСОНОМЕТРИЧЕСКИЕ ИЗОБРАЖЕНИЯ 97

7.1. Принцип аксонометрического проецирования 98

7.2. Виды аксонометрических проекций 100

7.3. Связь между коэффициентами искажений 100

7.4. Коэффициенты искажений прямоугольной аксонометрии 102

7.5. Приведенные коэффициенты искажения 102

7.6. Углы между аксонометрическими осями. Построение аксонометрических проекций геометрических элементов 103

Учебное издание


Савченко Нелли Вячеславовна

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Конспект лекций

Учебное пособие
Редакторская обработка Ю.Н. Литвинова

Компьютерная верстка Н.В. Савченко

Подписано в печать 14.06.2011. Формат

Бумага офсетная. Печать офсетная.

Печ. л. 10,0

Тираж 100 экз. Заказ . Арт. .


Самарский государственный

аэрокосмический университет

443086, Самара, Московское шоссе, 34.

Изд-во Самарского государственного

аэрокосмического университета

443086, Самара, Московское шоссе, 34.

1 См. п.1.2. Основные свойства параллельного проецирования.

2 См. п/п 2.2.1. Положение прямой относительно плоскостей проекций.

3 В системе трех плоскостей проекций плоскость общего положения имеет три следа.

4 См. п. 1.2

5 Задача принадлежности рассматривалась в п. 3.3.

6 См. п/п 3.6.3