Контрольная работа. Контрольная работа по дисциплине Теория информации
 Скачать 1.93 Mb. Скачать 1.93 Mb.
|
|
Расположим символы в порядке убывания количества их появления  Мы получили узлы (то есть наши символы – буквы), сверху в которых написано значение счётчика их появлений (сколько раз они встречаются во фразе). Выберем 2 узла с наименьшими значениями из конца списка «ь» и «я». У них у обоих значение равно 1. Создадим родительский узел (объединим их квадратиком сверху), значение счетчика которого равно 2 (сумме значений в кружочках снизу), и присоединим к нему два выбранных узла в качестве дочерних. Получим первое мини-дерево с корнем-квадратом (это родительский узел) 2 и ветвями 1 и 1. Поместим родительский узел обратно в пул (список). Повторим цикл с самого начала. На этот раз мы выбираем узлы «у» и «ф», объединяем их в мини-дерево, и помещаем родительский узел (значение счетчика которого снова равно 2) обратно в пул. Снова повторим цикл ещё 5 раз для следующих пар символов со счётчиком 1, Создавая для них родительский узел со счётчиком 2 и присоединяя их к нему в качестве дочерних. 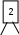 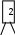 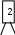 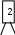          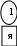  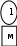 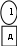  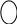 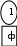  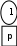   1 1    т о Снова повторим цикл. На этот раз в нашем распоряжении имеется десять узлов со значениями счетчиков, равными 2 (4 единичных и 6 родительских узлов, которые были добавлены перед этим) и три единичных узла со значением 3. Выберем узлы «л» и «ч» и снова добавим в пул родительский узел, значение счетчика которого равно 4. Также поступим с узлами «пробел» и «в». Выберем узел «а», присоединим его к узлу «и» и снова добавим в пул родительский узел, значение счетчика которого равно 6. Затем выберем два родительских узла (созданные в предыдущей схеме) со значениями счетчиков, равными 2, присоединим их к новому родительскому узлу со значением счетчика, равным 4, и добавим этот родительский узел в пул. 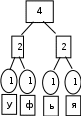 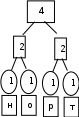 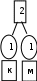 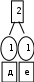 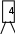 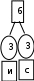 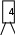      Выберем родительские узлы со значениями 4 и 4, присоединим их к новому узлу со значением 8. Таких узлов получилось 2. Выберем родительские узлы со значениями 2 и 2, присоединим их к новому узлу со значением 4.     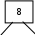 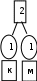 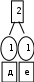 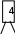 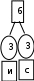 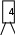      Выберем узел 3(символ «а») и присоединим его к родительскому узлу 4. Выберем родительские узлы со значениями 8 и 8, присоединим их к новому узлу со значением 16. Выберем родительские узлы со значениями 6 и 7, присоединим их к новому узлу со значением 13.   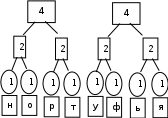 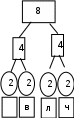    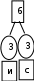 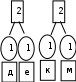 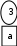 Выберем родительские узлы со значениями 13 и 16, присоединим их к новому узлу со значением 29. В результате получили результирующее дерево Хаффмана. 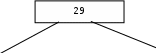   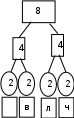   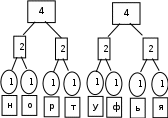  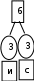 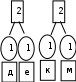 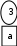 Для кодирования информации уберём лишние символы. Начиная с корня дерева (верхнего круга) на всех выходящих из кругов ветках слева напишем «0», а справа «1». Получили кодировочное дерево. 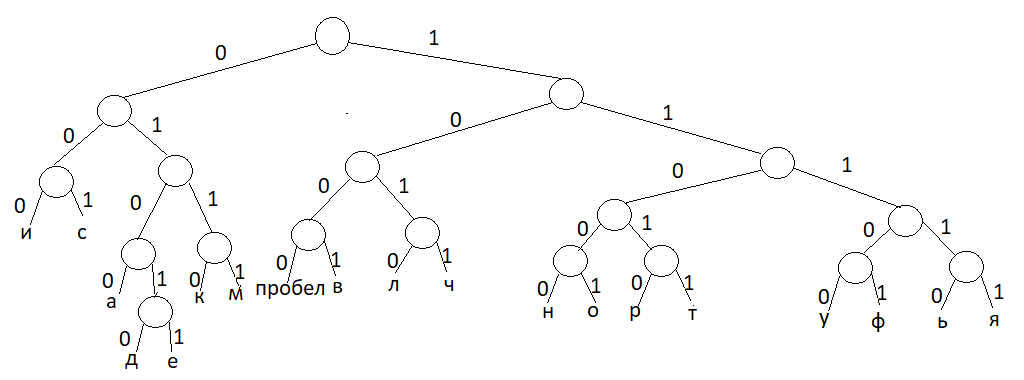 Переходя от одного узла (круга) к другому, начиная с самого верхнего, будем записывать цифры, по которым проходим. В результате получим код для каждого символа. Коды запишем в таблицу.
Теперь мы можем закодировать исходную фразу. 000 1010 11110 11111 001 01001 1001 000 1011 1000 0100 1010 01011 0110 001 0100 11000 01010 11010 1000 0111 11100 001 11011 0100 11101 11001 1001 000 1011 Ответ: 000 1010 11110 11111 001 01001 1001 000 1011 1000 0100 1010 01011 0110 001 0100 11000 01010 11010 1000 0111 11100 001 11011 0100 11101 11001 1001 000 1011. 7. На любой из позиций двоичного кода может быть с равной вероятностью переданы «0» и «1». Помехи преобразуют «1» в «0» с вероятностью 0,02 и «0» в «1» с вероятностью 0,04. Найти вероятность того, что был передан «1», если принят «1». Событие B1 - был передан ноль, событие B2 - была передана единица. Эти события несовместны и образуют полную группу. По теореме сложения вероятностей если два события несовместны, то вероятность наступления каждого из них равна сумме их вероятностей̆ P (X + Y) = P(X) + P(Y) – теорема сложения вероятностей. Значит P(B1) +P(B2) =1. Они имеют одинаковую вероятность, так как исхода всего 2, значит P (B1) = ½=0,5, P(B2) = ½=0,5. Гипотеза A - принята «1». Оно возможно только при условии, что исполнилось либо событие В1 – был передан «0», либо событие В2 – была передана «1». Нам благоприятствуют 2 исхода – была передана «1» и принята «1» (помехи не преобразовали «1» в «0»), и был передан «0» и принята «1» (помехи преобразовали «0» в «1»). События А/В1 – была принята «1» при переданном нуле и не А/В1 – был принят «0» при переданном «0» – противоположны, сумма вероятностей противоположных событий равна «1». Поэтому P(А/В1) + Р (не А/В1) =1. P(А/В1) =1-Р (не А/В1) =1- 0,04= 0,96 - «1» принята при переданной «1». P(А/B2) = 0,02 - «1» принята при переданном нуле. Теорема. Вероятность полного события, которое может произойти при осуществлении одного из несовместных событий, образующих полную группу, определяется формулой̆: P(X) = P(Y1)P(X /Y1) + P(Y2)P(X /Y2) + . . . + P(Yn)P(X /Yn) = 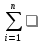 P(Yi )P(X /Yi ) P(Yi )P(X /Yi )Вероятность приема единицы по формуле полной вероятности, записанной выше P(A)= P(B1) *P(А/B1) + P(B2) *P(А/B2) = 0,5*0,96+ 0,5*0,02= 0,49. Вероятность А/В2 приёма «1», если передана «1» (то есть помехи не преобразовали «1» в «0») составляет с вероятностью не А/В2 приёма «0», если передана «1» (то есть помехи преобразовали «1» в «0») полную группу. Значит Р(А/В2)- Р (не А/В2) =1, Р(А/В2) =1-0,02=0,98. В случае, если событие, появляющееся совместно с каким-либо из несовместных событий, образующих полную группу, произошло и требуется произвести оценку вероятностей событий , применяется формула Байеса: 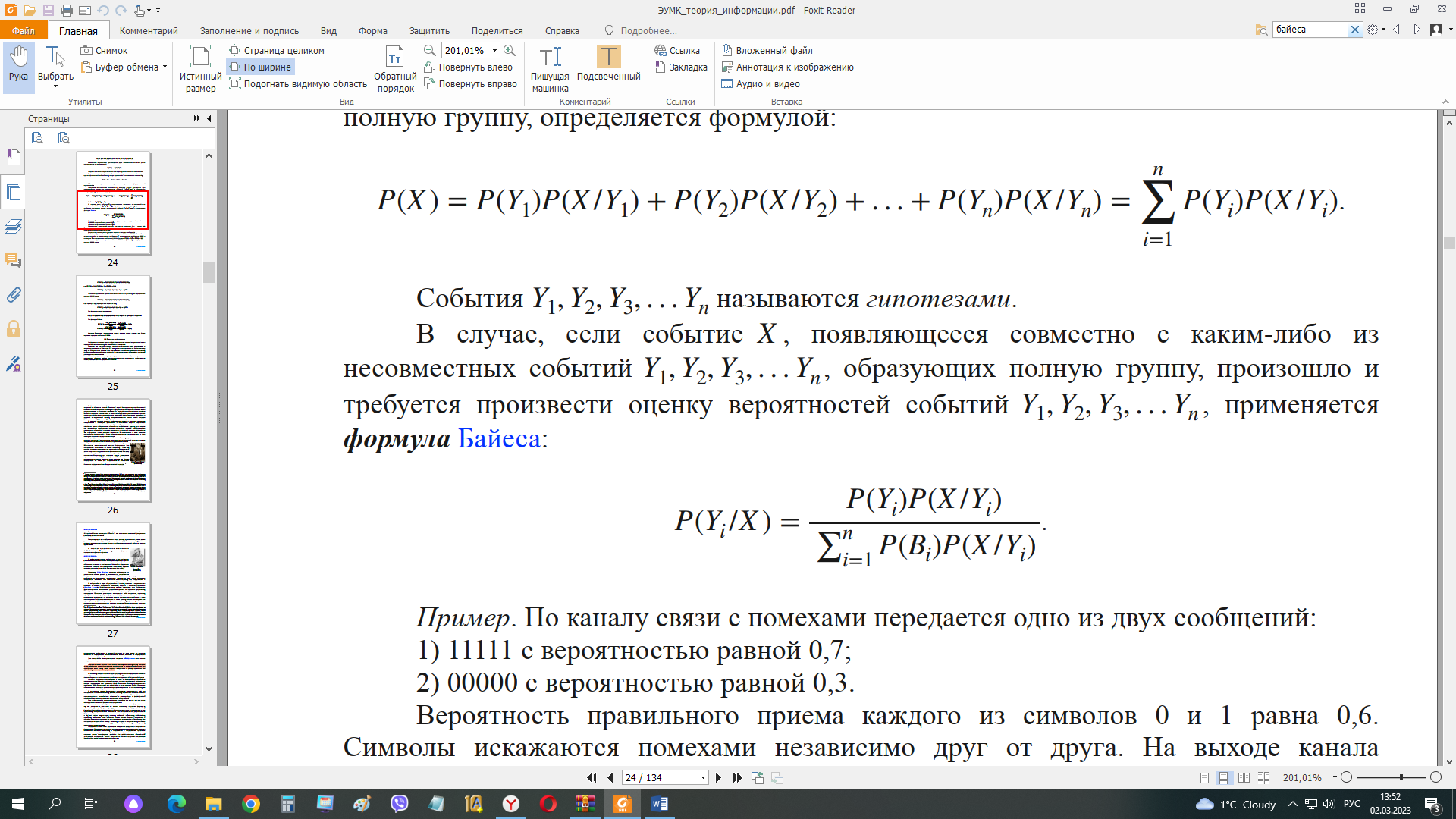 Теорема Байеса для нашего случая P(A|B2) = P(B2|A) * P(A)/P(B2) P(A|B2) – вероятность наступления события А, при условии, что событие В2 уже случилось (принята единица при переданной единице); P(B2|A) – вероятность наступления события В2, при условии, что событие А уже случилось (Передана единица, если принята единица). P(A) –вероятность наступления события А (принята 1); P(B1) –вероятность наступления события В2 (передана 1). Тогда P(B2|A) =P(A|B2) /P(A)*P(B2) =0,98/0,96*0,5=0,51 Ответ: вероятность того, что был передан «1», если принят «1» равна 0,51. 8. Используя теоретический материал зашифровать текст, используя квадрат Полибия, согласно вариантам (см. ниже). Регистр не учитывается. Красота до вечера, а доброта навек. 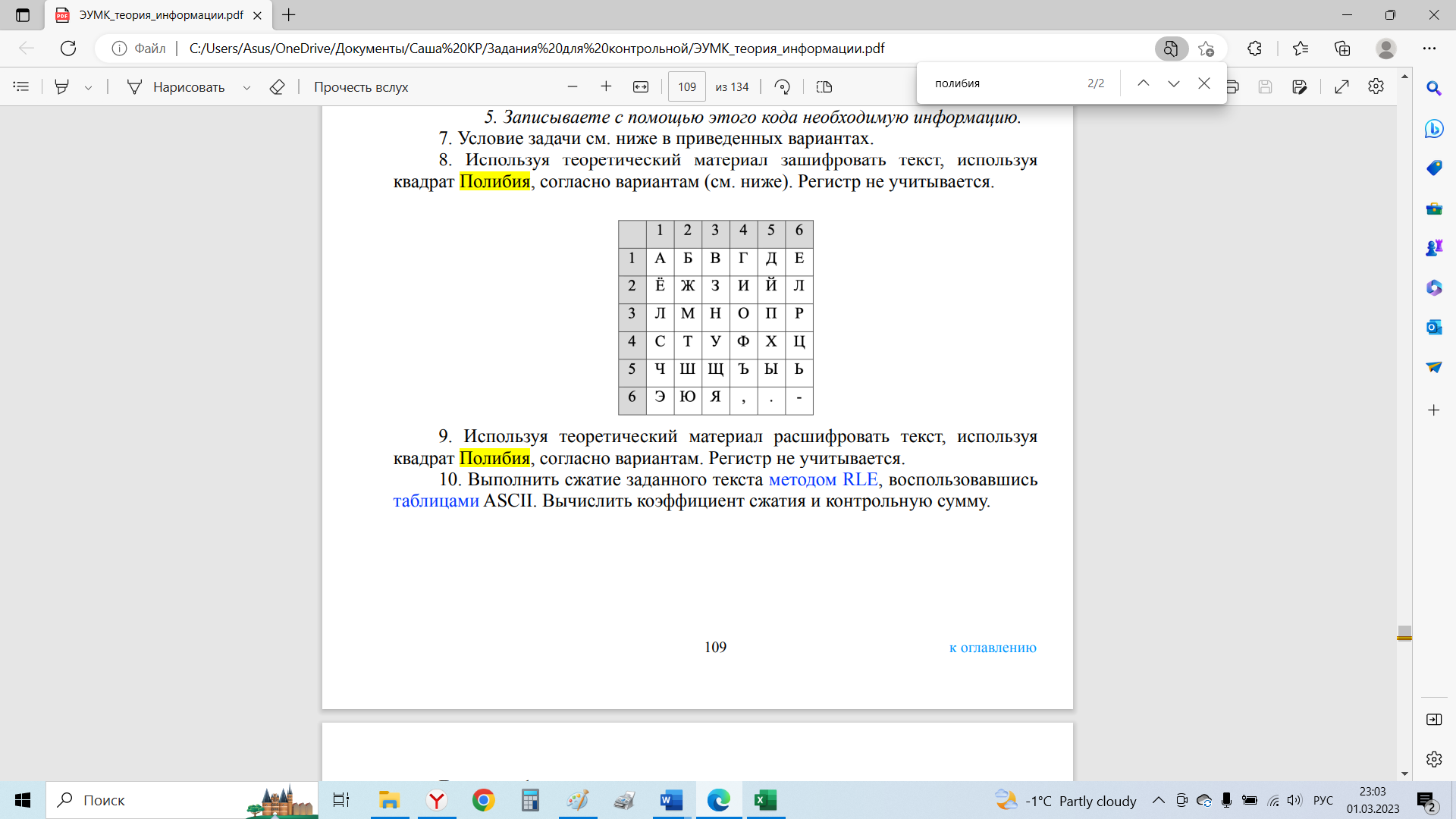 Решение. Шифрование с помощью квадрата Полибия производится следующим образом – каждой букве ставится в соответствие двузначное число, состоящее из номера строки и номера столбца. Так буква «К» шифруется числом 26, «Р» - 36 и т. д. Для удобства составим таблицу.
Выпишем коды в строку 26 36 11 41 34 42 11 15 34 13 16 35 34 36 11 64 11 15 34 12 36 34 42 11 33 11 1316 26 65 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
