Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
 Скачать 7.87 Mb.
|
Задача 3.1. Проверить, является ли одно из множеств А и В подмножеством другого. А = {х/х N,х  4};В= {х/х N, х 2}.2. Определить отношения между множествами, изобразить множества с помощью кругов Эйлера: А = {х/х N, х 9}; В = {х/х N, х 3}; С = {х/х N, х 6}.Решение. 1) Можно записать: А = {4, 8, 12, 16,...}, В= {2,4, 8, 10, 12, 14, 16,...}. Докажем, что А В. Согласно определению подмножества надо доказать, что любой элемент множества А принадлежит множеству В. Пусть а А, следовательно, а – натуральное и а 4, а это значит всегда а 2, поэтому а В. Множество В не является подмножеством А, так как из того что b 2 не всегда следует, что b 4.Пример: 6 : 2, но 6 не : 4. 2) Надо выяснить, какое из множеств будет подмножеством другого, или какие из них совпадают. Можно записать: А ={9, 18,27,36,...}; В= {0,3,6,9, 12, 15, 18,21,24,27,...}; С= {6, 12,18,24,...}. Любой элемент множества А принадлежит и множеству В, т.к. любое натуральное число, кратное 9, кратно 3, А В. Любой элемент из множества С принадлежит и множеству В, т.к. любое натуральное число, кратное 6, будет кратно 3, С В. Множества А и С имеют общие элементы, например 18, но и каждое из них имеет элементы, не принадлежащие другому. 9 А, но 9 С; 12 С, но 12 А. Круги для множеств А и С пересекаются, но оба они внутри круга для множества В (рис. 6). 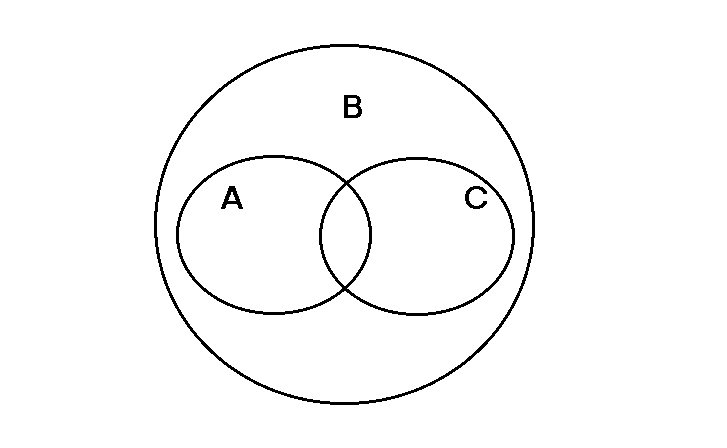 Рис. 6 Задача 4 Пусть А – множество четырехугольников плоскости, В – множество прямоугольников, С – множество ромбов, Д – множество четырехугольников, имеющих прямой угол.
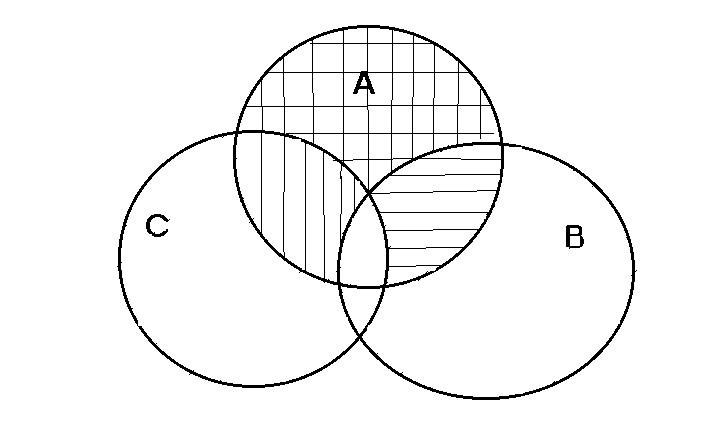
MNLK X и FSQP X N L S Q   M K F P 1) Решение Для совокупности множеств А, В, С, Д множество А можно считать универсальным, т.к. множества В, С, Д являются подмножествами множества А. Д'– дополнение множества Д до универсального, т.е. до множества А. Д'– множество четырехугольников, не имеющих прямого угла. Д' С – пересечение множеств Д и С, это множество четырехугольников, не имеющих прямого угла и являющихся ромбами. Так как ромб, имеющий прямой угол, это квадрат, то получаем: Х = Д' С - множество ромбов, не являющихся квадратами. 2) А – универсальное множество, изображаем его в виде прямоугольника. Круги для множеств В,Д,С- внутри прямоугольника. Круги для множеств В и С пересекаются, т.к. есть прямоугольники, являющиеся ромбами, – квадраты. Круг для множества В внутри круга для множества Д, т.к. В Д. Д' – заштрихуем горизонтальной штриховкой, С – заштрихуем вертикальной штриховкой, Х = Д' С – та часть, которая заштрихована дважды. 3) МNLК Х - ложное высказывание, FSQP Х – истинное высказывание. 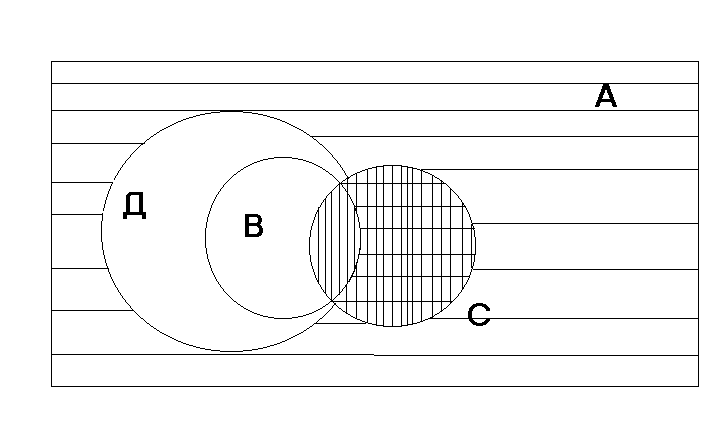     Задача 5Найти А В, А В, А\В, В\А, и А', если И = К, А = [-2,8]; В= [0,9].  Из рисунка видим: АВ = [-2,9, А В = [0,8], А\В = [-2, 0), (0 А\В, т.к. 0 А и 0 В), В\А = (8, 9], (8 В\А, т.к. 8 А), А1 = ( -, - 2) (8, + ). Задача 61) Доказать, что для любых множеств А, В, С верно равенство А\(ВС ) = (А\В) (А\С). 2) Проиллюстрировать это равенство геометрически. Решение. 1) Обозначим: М = А\(В С), К = (А\В) (А\С). Для доказательства равенства М = К достаточно доказать утверждения: а) М К, т.е. для любого х, если х М, то х К; б) К М , т.е. для любого х, если х К, то х М. в) Пусть любое х А\(В С). По определению разности двух множеств х А и х (В С). Если бы х принадлежал хотя бы одному и множеств В и С, то, по определению объединения, х принадлежал бы В С. Поэтому из того, что х В С, следует, что х В и х С. Так как х А и х В, то х А\В. Так как х А и х С, то х А\С. По определению пересечения множеств, х (А\В) (А\С). г) Пусть любое х (А\В) (А\С). По определению пересечения множеств, х А\В и х А\С. По определению разности множеств х А, xВ, xС. Тогда х В С. А так как х А и х В С, то x А\(В С) . Вывод: М К и К М, тогда М = К. 2) Изобразим множества А, В и С. Сделаем два одинаковых рисунка, на одном выделим множество М, на другом множество К.
Контрольные вопросы
а) множества четных чисел, б) множества нечетных чисел. |
