Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
 Скачать 7.87 Mb.
|
|
ПРЕДИСЛОВИЕ Успешное обучение математике младших школьников требует от учителя не только методического мастерства, но и глубокого понимания сути математических понятий и фактов. Это предъявляет особые требования к математической подготовке учителя начальной школы. Учителю необходимо и умение использовать уроки математики для воспитания учащихся, в частности, для формирования у них основ научного мировоззрения. Данное учебное пособие написано в соответствии с государственным образовательным стандартом высшего профессионального образования. Оно нацелено на решение задачи обеспечения будущего учителя начальных классов базовыми математическими знаниями, необходимыми ему для грамотного, творческого обучения и воспитания младших школьников, для дальнейшей работы по углублению и расширению математических знаний. Структура пособия такова: весь материал разбит на 5 глав, главы – на небольшие разделы. В начале каждого раздела излагается необходимый справочный материал, затем приводятся разнообразные образцы заданий с подробными решениями. В конце каждой главы – контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы. Профессиональная направленность пособия достигается посредством определенного отбора теоретического материала, а также включения заданий, выполняемых младшими школьниками. Эти материалы взяты, в основном, из действующих учебников по математике для начальных классов. В пособии приведены задания для контрольных работ, которые преподаватель может использовать на аудиторных занятиях. I. МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ Литература [1] гл. 1, §1
Понятие множества является одним из основных понятий математики. Понятия «множество», «элемент», «элемент, принадлежащий множеству», являются первичными неопределяемыми понятиями. Содержание этих понятий можно объяснить на примерах. Так, можно говорить о множестве жителей города, о множестве учащихся некоторой школы, о множестве натуральных чисел и т.д. В повседневной жизни вместо слова «множество» употребляют слова «набор», «совокупность», «коллекция» и т.д. Один из создателей теории множеств Г. Кантор (Георг Кантор, 1845-1918, немецкий математик), писал: «Множество есть многое, мыслимое как единое, целое». Объекты любой природы (люди, буквы, числа и т.д.), составляющие множество, называются его элементами. Множество обычно обозначают большими буквами латинского алфавита, а их элементы малыми, «принадлежит» заменяют символом . Высказывание «объект а принадлежит множеству А» записывают так: а А. Высказывание «элемент а не принадлежит множеству А» записывают так: а А или а  А.Для некоторых числовых множеств имеются специальные обозначения. Так, множество всех натуральных чисел обозначают буквой N, всех целых чисел – Z, множество всех рациональных чисел – Q, множество всех действительных чисел – буквой R. Множества могут содержать как конечное число элементов, так и бесконечное. Так, множество предметов, изучаемых в школе, конечно, а множество точек прямой бесконечно. Рассматривают в математике и множество, не содержащее ни одного элемента, его называют пустым множеством и обозначают символом . Примерами пустого множества могут служить: множество людей на Солнце, множество действительных корней уравнения х2 + 1 = 0
Множество считают заданным, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит. Существует несколько способов задания множеств.
3) Задание множества с помощью характеристического свойства элементов множества. Этот способ заключается в том, что если хотят задать множество А, то: а) указывают хорошо известное множество М, подмножеством которого является множество А; б) указывают свойство Р, которым обладают те и только те элементы множества М, которые входят в А. При этом множество А записывают в виде: А = {х/х М, Р(х)}, где символ Р(х) заменяет слова: «элемент х обладает свойством Р». Например, А – множество натуральных чисел, меньших 6 можно задать так: А = {х/х N, х < 6}. _______________________________________________________________ Определение 1. Множества А и В называются равными, если они состоят из одних и тех же элементов. В этом случае пишут, А=В. _________________________________________________________________________________________ Например: А = {12, 22, З2, 42 }и В = {  } равны, А = В, т.к. оба множества состоят из чисел 1, 4, 9, 16.______________________________________________________________ Определение 2. Множество В называют подмножеством множества А, если каждый элемент множества В является одновременно и элементом множества А. В этом случае пишут В А. __________________________________________________________________________ Согласно данному определению подмножества каждое множество является подмножеством самого себя: А А. Кроме того, считают, что пустое множество есть подмножество любого множества А: А. Определение 3. Если А В и А В, то А называют собственным подмножеством множества В _________________________________________________________________________________________ Например, множество А = {п,т,р} имеет восемь подмножеств: {т}, {n}, {р}, {т,р}, {т,п}, {п,р}, {n, т,р} и . Из определений 1 и 2, очевидно, что если В А и А В, то А = В. Из этого утверждения вытекает один из способов доказательства равенства двух множеств: если доказано, что любой элемент из В является элементом из А и, в свою очередь, любой элемент из А является элементом В, то делают вывод А= В. Кроме того, если А В и В С, то А С. Действительно, если, каждый элемент множества А принадлежит В, а каждый элемент множества В является, в свою очередь, элементом С, то каждый элемент из А принадлежит множеству С. Чтобы наглядно изображать множества и отношения между ними, рисуют геометрические фигуры, которые находятся между собой в этих отношениях. Например, если мы хотим наглядно изобразить, что множество А является собственным подмножеством В, то рисуем эти множества так, как показано на рисунке 1. Если же надо показать, что множества А и В не имеют общих элементов, то их изображаем так, как показано на рисунке 2. Такие изображения множеств кругами называют диаграммами Эйлера-Венна. 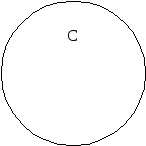 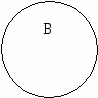  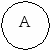 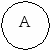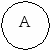Рис. 1 Рис. 2 Рис. 3. Диаграмма, показанная на рисунке 3, делает очевидным утверждение: если А В и В С, то А С. ____________________________________________________________ Определение 4. Для данных множеств А, В С,... универсальным множеством называют каждое множество И, такое, что А И, В И, С И,... ______________________________________________________________________________________ Каждое множество является универсальным множеством для любой системы своих подмножеств. Например, если А – множество студентов первого курса некоторого института, В – множество студенток в этом же институте, С – множество спортсменов этого же института, то в качестве универсального множества И можно взять множество всех студентов данного института, тогда А И, В И, С И. 3. ОБЪЕДИНЕНИЕ И ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ, ИХ СВОЙСТВА _____________________________________________________________ Определение 5. Объединением двух множеств А и В называется множество, состоящее из элементов, которые принадлежат, хотя бы одному из этих множеств. _____________________________________________________________________________________ Объединение множеств А и В обозначают А В, где символ знак объединения множеств, А В = {х/х А или х В}. Например, А = {1,2,3,4}, В = (3,4,5,6},АВ={1,2,3,4,5,6}. Н  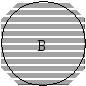 а диаграмме Эйлера-Венна заштриховано объединение множеств А и В.О  чевидно, что хАВ тогда и только тогда, когда х А и х В. Операция объединения множеств обладает следующими свойствами:
А В = В А (коммутативность). 2. Для любых множеств А, В и С имеем: (А В) С = А (В С) = А В С (ассоциативность). 3. Если В А, то АВ = А. В частности, для любого множества А имеем: А А=А; А=А; АИИ. Проиллюстрируем некоторые свойства с помощью диаграмм Эйлера:  И   Заштриховано объединение множеств А В и А И ____________________________________________________________ Определение 6. Пересечением множеств А и В называют множество, состоящее из всех тех и только тех элементов, которые одновременно принадлежат и множеству А, и множеству В. ____________________________________________________________________________________ Пересечение множеств А и В записывают А В, где - знак пересечения множеств. А В = {х/х А и х В}. Например: А = {1,2, 3,4}; 5= {3,4, 5, 6}; А В = {3,4}. На диаграмме Эйлера-Венна заштриховано пересечение множеств А и В. 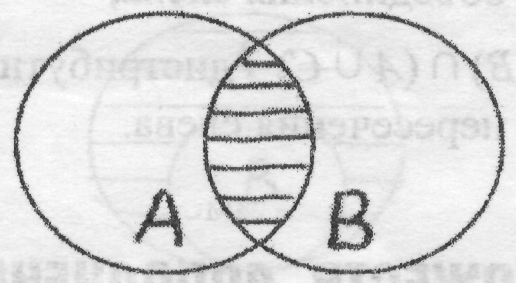 Очевидно, что х А В тогда и только тогда, когда х А или х В. Операция пересечения множеств обладает следующими свойствами:
А В = В А (коммутативность).
(АВ) С = А (ВС)=АВ С (ассоциативность). 3. Если А В ,то А В = А. В частности, для любого множества А имеем А А = А; А = ; А И = А. Проиллюстрируем третье свойство с помощью диаграмм Эйлера-Венна. 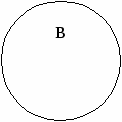 И 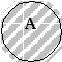 На рисунках заштриховано пересечение множеств А В и А И. Операции объединения и пересечения множеств связаны дистрибутивными законами:
4. РАЗНОСТЬ МНОЖЕСТВ. ДОПОЛНЕНИЕ К ПОДМНОЖЕСТВУ _______________________________________________________________ Определение 7. Разностью множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат множеству А, но не принадлежат множеству В. _________________________________________________________________________________________ Операция нахождения разности двух множеств называется вычитанием множеств. Разность множеств А и В обозначают символом А\В. Таким образом, по определению, А\В = {х/х А и х В}.  |