Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
 Скачать 7.87 Mb.
|
|
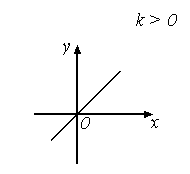
Задача 2. X Y 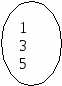 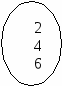       Между элементами множеств Х = {1,3,5} и Y = {2,4,6} задано соответствие р – «меньше». Задать соответствие перечислением пар, построить граф соответствия, указать образ 1 Хи прообраз 4 Y. Решение. Р={(1, 2); (1, 4); (1, 6); (3, 4); (3, 6); (5,6)}. Образ1 Х, p(1)= {2, 4, 6}. Прообраз 4 Y= {1,3}. 2. ФУНКЦИИ Функция – одно из важнейших понятий математики. __________________________________________________________________ Определение 5. Числовой функцией называется такое соответствие между числовым множеством X и множеством действительных чисел R, при котором каждому числу множества X соответствует единственное число из множества R. _____________________________________________________________________________________________ Множество Xназывают областью определения функции. Функции принято обозначать буквами f, g, hи др. Если f – функция на множестве X, то действительное число у соответствующее числу х из множества X, часто обозначают f(х) и пишут у= f(х). Переменную х при этом называют аргументом (или независимой переменной), а у – функцией. Множество чисел вида f(x) для всех х из множества Х называют областью значений функции f. Часто функции задают с помощью формул y = f(х), указывающих как по данному значению аргумента найти соответствующее значение функции. Иногда при задании функции с помощью формулы ее область определения не указывается. Втаких случаях считают, что областью определения функции является область определения выражения f(x) (множество допустимых значений выражения f(x)). Кроме формул, функции могут быть заданы: - при помощи таблицы; - графически. Графиком функции у = f(х) с областью определения Xявляется множество таких точек координатной плоскости, которые имеют абсциссу х и ординату f(х) для всех х из множества X. Не каждое множество точек на координатной плоскости представляет собой график некоторой функции. Например, 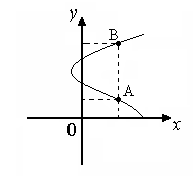 Линия не является графиком функции. Функции могут обладать многими свойствами, одно из которых – монотонность. __________________________________________________________________ Определение 6. Функция f называется монотонной на некотором промежутке А, если она на этом промежутке возрастает или убывает. _____________________________________________________________________________________________ __________________________________________________________________ Определение 7.Функция f называется возрастающей на некотором промежутке А, если для любых чисел X1 и Х2 из множества А выполняется условие: х, < х2=> f(x1) < f(х2) (большему значению аргумента соответствует большее значение функции). _____________________________________________________________________________________________ __________________________________________________________________ Определение 8.Функция f называется убывающей на некотором промежутке А, если для любых чисел x1, х2 из множества А выполняется условие: x1 < х2 =f(x1) > f(х2) (большему значению аргумента соответствует меньшее значение функции). ____________________________________________________________________________________ Пример 4. Функция задана аналитически (формулой) у = 2х + 1. 1. Построить график функции, если ее область определена а) Х = [– 0; 2]; б) Х = {– 2, – 1, 0, 1,…}; в) X = R 2. Исследовать на монотонность 1  ). Построить график функций: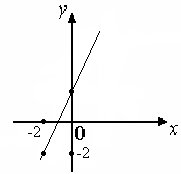 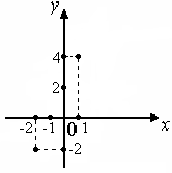 а) б) в) 2) исследуем функцию на монотонность. Пусть х1 < х2 f(x1)= 2x1 + 2 и f(x2) = 2x2 + 2. Найдем разность f(x1) – f(x2)= (2x1 + 2)–( 2x2 + 2) =(2x1 – 2x2)+ 2 – 2 = 2 (x1 – x2)<0, т.к.x1 < x2; f(x1) – f(x2)<0 f(x1) < f(x2) Получили: x1 < x2 f(x1) < f(x2), по определению (6) функция у = 2х + 2 возрастающая. __________________________________________________________________ Определение 9. Прямой пропорциональностью называется функция вида у =kх, где k 0 и k – действительное число. _____________________________________________________________________________________________ Если отношение двух величин равно некоторому числу, отличному от нуля, их называют прямо пропорциональными. В нашем случае  ( k 0), k – коэффициент пропорциональности.Некоторые свойства прямой пропорциональной зависимости.
 
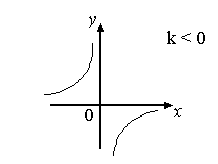
__________________________________________________________________ Определение 10. Обратной пропорциональностью называет функция вида у =  , где к – не равное нулю действительное число._____________________________________________________________________________________________ Если произведение двух величин равно некоторому числу, отличному от нуля, то эти величины называют обратно пропорциональными. В нашем случае х у = k(k 0), k – коэффициент пропорциональности. Некоторые свойства обратной пропорциональной зависимости
 
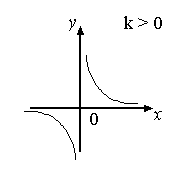
___________________________________________________________________ Определение 11. Функция, которая может быть задана при помощи формулы у = kх + с, называется линейной, k 0. ______________________________________________________________________________________________ Некоторые ее свойства: 1. Областью определения и областью значений функции является множество действительных чисел. 2. Графиком является прямая, пересекающая ось ОYв точке с ординатой с. 3. При k > 0 функция возрастает на всей области определения, при k < 0 – убывает на всей области определения. Задача 4. Задания для младших школьников: 1. Увеличить каждое четное однозначное натуральное число в 2 раза. 2. Заполнить таблицу:
Функции, приведенные в этих пунктах, задайте при помощи формул и укажите для каждой область определения и множество значений. Решение: 1. Четные однозначные числа 2, 4, 6, 8.Увеличиваем каждое из них в 2 раза: 4, 8, 12, 16. Задаем формулой у = 2х. Область определения Х= {2, 4, 6, 8}. Множество значений Y = {4, 8, 12, 16}. 2. Заполняем таблицу
Задаем функцию формулой  Область определения X= {1, 2, 4, 8}. Множество значений Y = {1,2,4, 8}. Основными свойствами прямой и обратной пропорциональности можно пользоваться при решении текстовых задач. Задача 5. Из куска ткани длиной 20 м в мастерской сшили 5 одинаков костюмов. Сколько потребуется ткани на 15 таких же костюмов? Решение: В задаче идет речь о расходовании ткани на костюмы. Этот процесс характеризуется тремя величинами: количеством (в данном случае надо говорить о длине, но в таких ситуациях чаще употребляется слово «количество») ткани, расходуемой на один костюм, количеством костюмов и количеством ткани, израсходованной на все костюмы. Согласно условию задачи количество ткани, расходуемой на один костюм, не меняется. Обозначим его буквой k. Количество костюмов х иколичество израсходованной на них ткани у изменяются, они связаны между собой зависимостью у = kx, т.е. зависимость количества ткани, израсходованной на костюмы, от количества костюмов прямо пропорциональная. Прямая пропорциональность является математической моделью ситуации, представленной в задаче. Запишем основное свойство этой зависимости  .Решим задачу двумя арифметическими способами: 1 способ: 2 способ:
Решая задачу первым способом, сначала нашли количество ткани, расходуемой на один костюм, – коэффициент к. Затем, зная что у = 4х, нашли значение у при условии, что х = 15. При решении задачи вторым способом воспользовались основным свойством прямой пропорциональной зависимости: во сколько раз увеличивается количество костюмов, во столько же раз увеличивается количество ткани, израсходованной на их изготовление. Задача 6. Мастер делает 6 деталей за 1 час, а ученик – 2 детали. Мастер сделал 48 деталей. Сколько деталей сделает ученик за это же время ? Решение: В задаче рассматриваются величины: время, производительность труда – количество деталей в 1 час, работа – количество всех деталей,сделанных мастером или учеником. Первая величина – время – постоянная, а две другие принимают различные значения. Составим таблицу:
Работа и производительность труда находятся в прямой пропорциональной зависимости. Если работу обозначим буквой А, время – t, производительность труда – p, то получим А = = t р, а отношение А : р = t – постоянная. В задаче надо найти работу, следовательно, А – функция. Производительности труда уученика и умастера разные, значит р – аргумент, время t постоянно – , это коэффициент пропорциональности. Обозначим время работы буквойk, работу – у, производительность х, тогда получим  или у = kх, т.е. математической моделью ситуации в задаче является прямая пропорциональность.Решим задачу двумя арифметическими способами: 1 способ: 2 способ:
Решив задачу первым способом, мы нашли сначала время работы мастера и ученика – коэффициент пропорциональности k, он равен 6. Затем, зная, что А = 8 2 = 16, нашли значение А при условии, что р = 2. При решении задачи вторым способом воспользовались основнымсвойством прямой пропорциональной зависимости: во сколько раз производительность ученика меньше производительности мастера, во столько же раз меньше деталей сделает ученик. |
. Если х > 0 и у > 0, то основное свойство обратной пропорциональной зависимости, сформулировать можно так: с увеличением (уменьшением) значения аргумента х в несколько раз соответствующее значение переменной у уменьшается (увеличивается) во столько же раз.