|
|
Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
6. МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
В математике, как и других науках, мы имеем дело с понятиями. Условимся обозначать их через а, b, с,... и т.д.
Всякое понятие характеризуется объемом и содержанием.
Объем понятия – это множество всех объектов, обозначаемых одним термином.
Содержание понятия – это множество всех существенных свойств объекта, отраженных в этом понятии.
Условимся объем понятия а обозначать через А, объем понятия b через В.
Отношения между понятиями
Если объемы понятий а и bне пересекаются, т.е. если А B = , то понятия а и bнесовместимы.
Если объемы понятий а иbнаходятся в отношении пересечения, т. е. А B , то понятия а и bсовместимы.
Если объем понятия а является собственным подмножеством объема понятия b, т.е. А В и А В, то говорят, что:
1) понятие а является видовым по отношению к понятию b; понятие b – родовым по отношению к понятию а;
2) понятие а уже понятия b, а понятие bшире понятия а;
3) понятие а есть частный случай понятия b, а понятие bесть обобщение понятия а.
Если объем понятия а равен объему понятия b, то говорят, что понятия а иbтождественны.
Большую роль в математике играют определения понятий. Во всяком понятии выделяют определяемое и определяющее понятия. Например, в предложении «Прямоугольником называется параллелограмм с прямым углом» определяемое понятие – «прямоугольник» (т.е. что определяется), а определяющее понятие – «параллелограмм с прямым углом» (т.е. то, через что определяется данное понятие).
Между определяемым и определяющим понятиями ставится знак  , который читается «равносильно по определению». Данное нами определение можно записать так: «прямоугольник , который читается «равносильно по определению». Данное нами определение можно записать так: «прямоугольник  параллелограмм с прямым углом». параллелограмм с прямым углом».
Одним из видов определений является определение через род и видовое отличие. Структура таких определений такова: в определяющем понятии указывается: 1) родовое по отношению к определяемому понятие и 2) то свойство, которое выделяет нужный нам вид из других видов данного нам рода (так называемое видовое отличие). Так, в рассмотренном выше примере родовым понятием является понятие «параллелограмм», а видовым отличием – свойство «иметь прямой угол».
Определение понятия через род и видовое отличие можно изобразить схематически.
определяемое понятие
родовое понятие
видовое отличие

Задача 10.
Дайте определение прямоугольника, указав в качестве родового понятия понятие «параллелограмм». Используя данное определение выясните правильность следующих обоснований:
а) Четырехугольник АВСД – прямоугольник, т.к. в нем есть прямой угол.
б) Четырехугольник ЕFKL – не прямоугольник, т.к. он не является параллелограммом.
Решение.
Множество прямоугольников можно выделить из множества параллелограммов с помощью свойства «иметь прямой угол». Таким образом, получаем определение: «Прямоугольником называется параллелограмм, имеющий прямой угол».
Для оценки правильности обоснований выделим логическую структуру данного определения. С этой целью обозначим через А утверждение «четырехугольник-прямоугольник», через В – «четырехугольник – параллелограмм», а через Р – «четырехугольник имеет прямой угол». Тогда определение примет вид: А  В Р. В Р.
Так как свойства В и Р связаны конъюнкцией, то вывод о том, что четырехугольник-прямоугольник, возможен лишь в том случае, когда оба утверждения истинны, т.е. на основании того, что четырехугольник параллелограмм и что в нем есть прямой угол. В данном обосновании есть указание на то, что в четырехугольнике АВСД имеется прямой угол, но не сказано, что АВСД – параллелограмм, этого не достаточно, чтобы утверждать, что АВСД – прямоугольник. Следовательно, данное обоснование неправильно.
Для того чтобы можно было сделать вывод о том, что четырехугольник не является прямоугольником, достаточно убедиться в том, чт о хотя бы одно из утверждений В или Р ложно, т.е. в том, что четырехугольник не является параллелограммом или что в нем нет прямого угла. Так как в данном обосновании есть указание на то, что четырехугольник ЕFKL не является параллелограммом, то этого достаточно, чтобы утверждать, что ЕFKL – не прямоугольник. Следовательно, обоснование б) правильно.
умозаключения
Большую часть знаний об окружающей нас действительности получаем с помощью рассуждений. В логике вместо термина суждение» чаще используется в качестве его синонима слово «заключение». Умозаключение – это способ получения нового знания на основе некоторых имеющихся. Умозаключение состоит из посылок и заключения. Посылки – это высказывания, содержащие исходное знание. Заключение – это высказывания, содержащие новое знание, полученное из исходного.
В умозаключении из посылок выводится заключение. В словесных формулировках заключение отделяется от посылок с помощью слов «следовательно», «значит» и др. Для удобства договорились записывать умозаключение с посылками А1, А2,..., Аии заключением В в виде 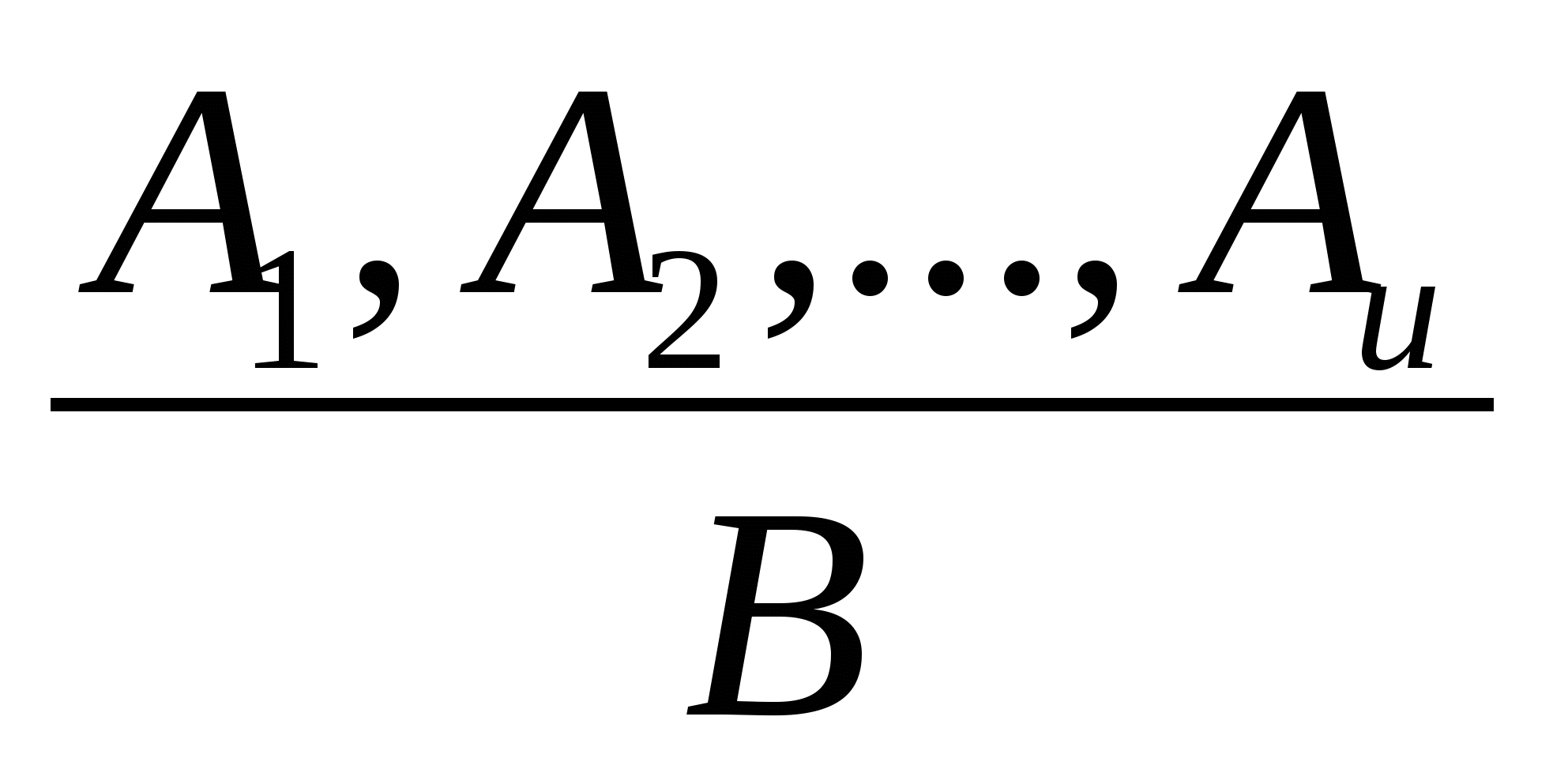 . В ней черта заменяет слово «следовательно». . В ней черта заменяет слово «следовательно».
Умозаключения делятся на дедуктивные (правильные) и недедуктивные (неправильные). Правильными называются умозаключения, в которых посылки и заключение находятся в отношении логического следования. Неправильными называются все умозаключения, в которых нет логического следования между посылками и заключением.
Наиболее часто встречающиеся схемы правильных умозаключений (в математике они называются правилами вывода).
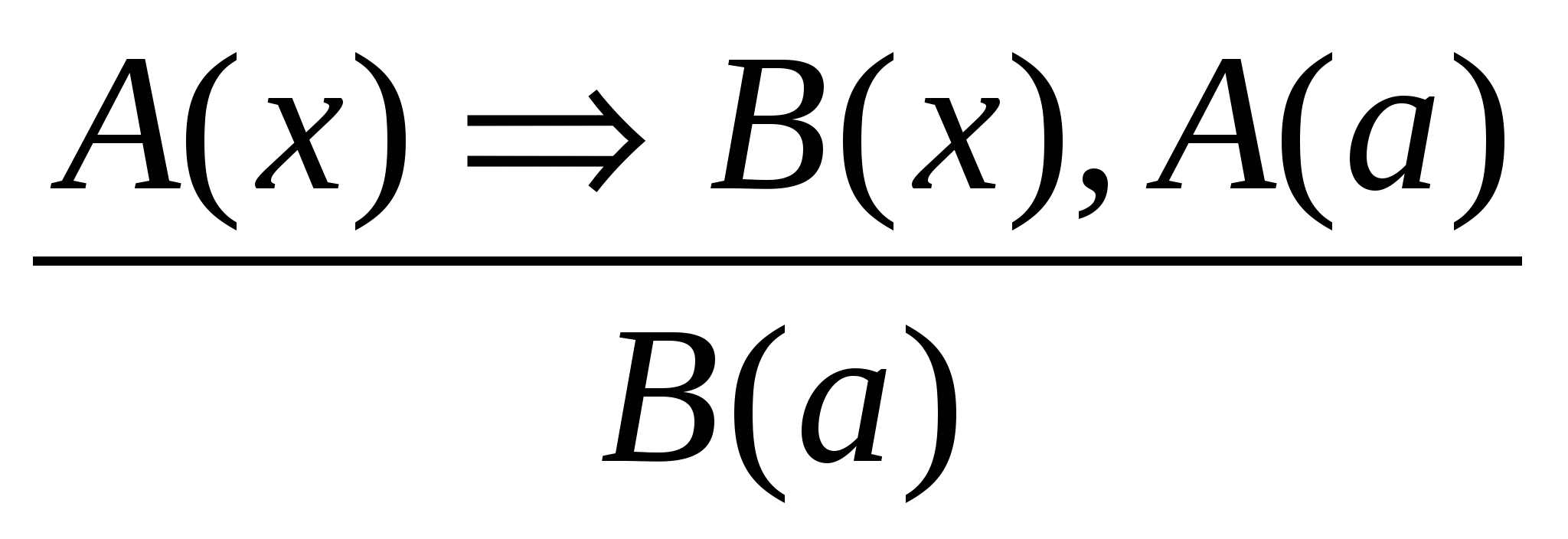
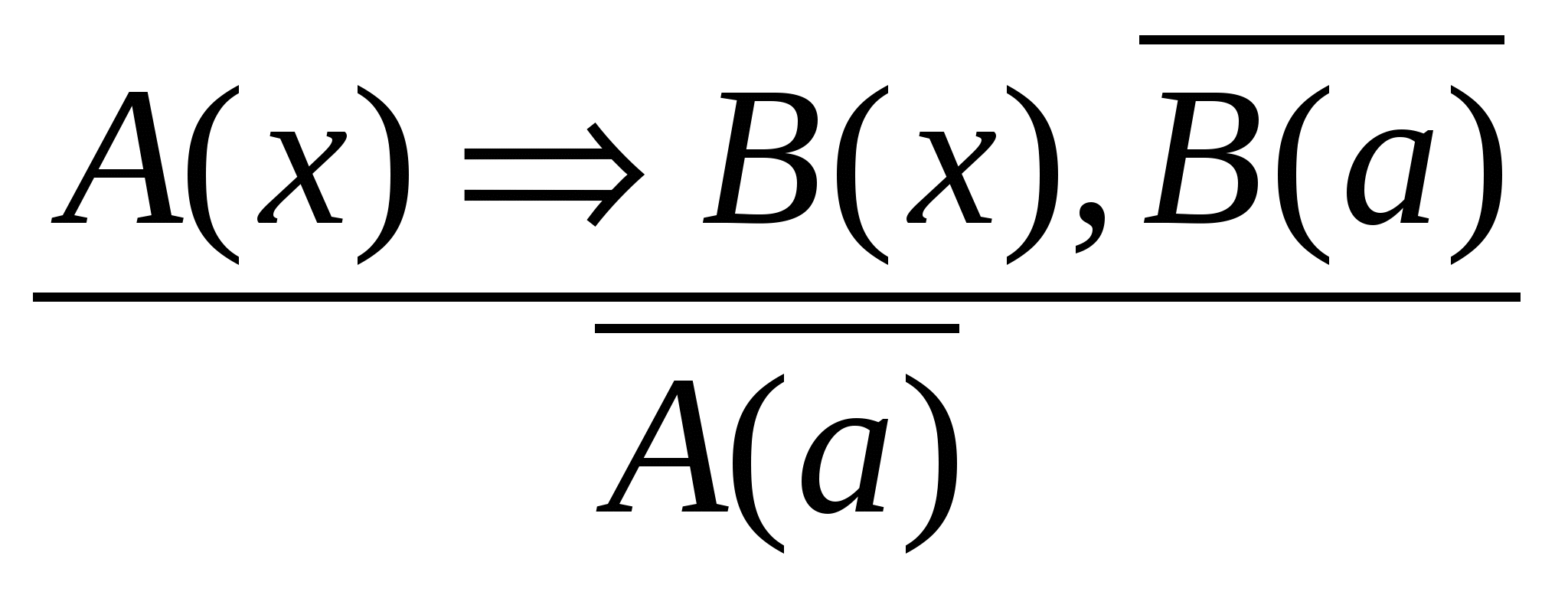
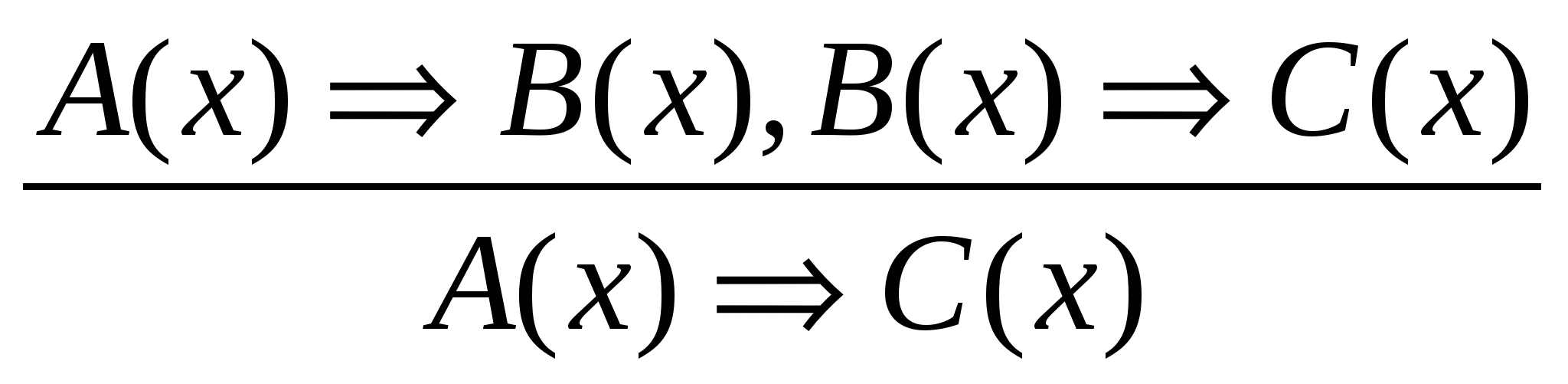
Выполняя рассуждения по этим правилам, мы всегда будем получать истинное заключение. Приведем пример умозаключения, выполненного по правилу заключения:
«Если запись числа х оканчивается четной цифрой, то число х делится на 2. Запись числа 126 оканчивается четной цифрой 6, следовательно, число 126 делится на 2».
В качестве общей посылки в этом умозаключении выступает утверждение вида «если А(х), то В(х)», где А(х) – это «запись числа х оканчивается четной цифрой», а В(х) – «число х делится на 2». Частная посылка представляет собой высказывание, которое получилось из условия общей посылки при х = 126 (т.е. это А(126)). Заключение является высказыванием, полученным из В(х) при х = 126 (т.е. это В(126)). Таким образом, форма данного умозаключения такова: 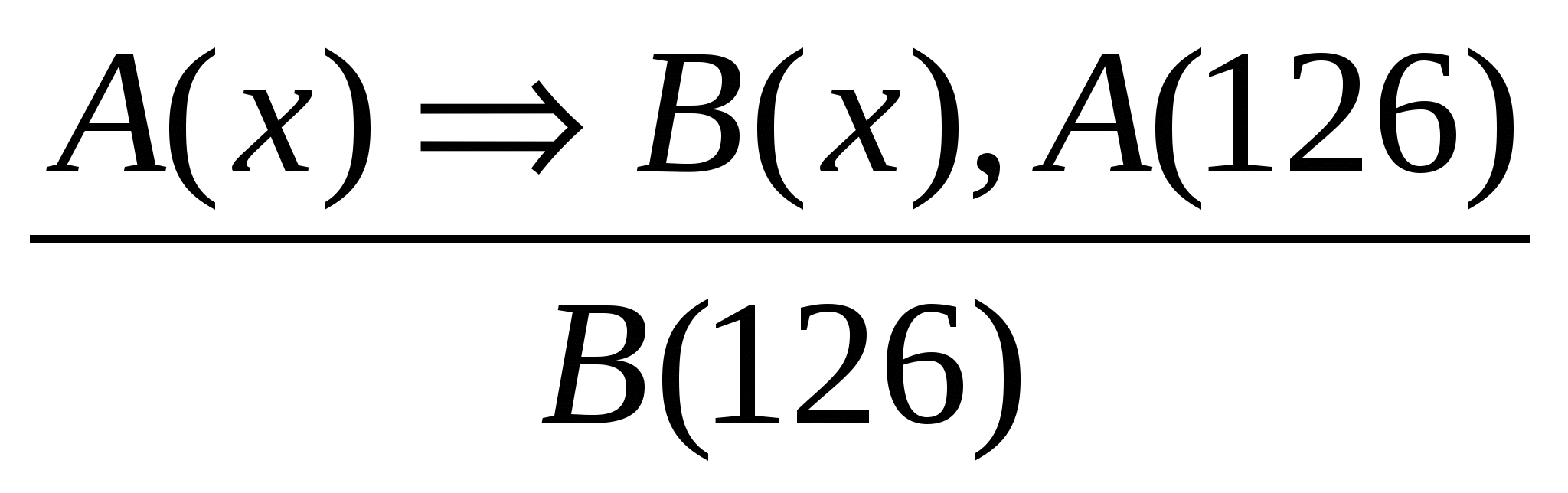
Истинность умозаключений, выполненных по правилам заключения, отрицания и силлогизма, можно показать, если записать правила на теоретико-множественном языке. Покажем, например, что умозаключение, выполненное по правилу силлогизма, является правильными.
Посылка А (х) => В(х) может быть записана в виде ТА ТВ, где ТАи ТВ – множества истинности предикатов А(х) и В(х). Посылка В(х) => С(х) может быть записана в виде ТВ ТС, где ТВ и ТС – множества истинности предикатов В(х) и С(х). Заключение А (х) => С(х) можно записать в виде ТА ТС.
Всё умозаключение, построенное по правилу силлогизма, запишется на теоретико-множественном языке так:
   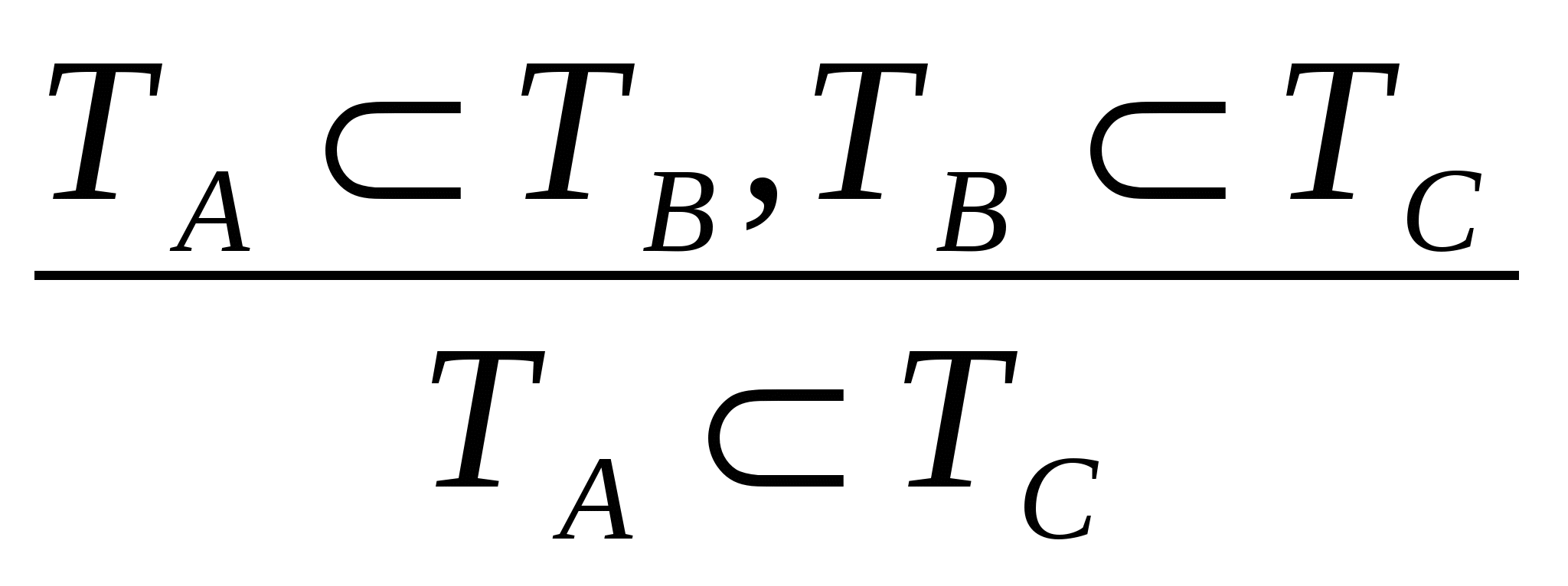
Изобразив на кругах Эйлера множества ТА , ТВ , ТС, мы видим, если ТА ТВи ТВ ТС , то ТА ТС.
Контрольные вопросы
Дайте определение
а) объема понятия;
б) содержания понятия.
Какие виды понятий вы знаете? Назовите понятия, относящиеся к каждому виду.
Назовите способы определения понятий и перечислите основные требования к ним.
Что называется умозаключением?
Какое умозаключение называется дедуктивным?
Записать правила:
а) заключения; б) отрицания; в) силлогизма.
7. Изобразить с помощью кругов Эйлера правила: а) заключения; б) отрицания.
Упражнения
211. Дайте определение прямоугольника, указав в качестве родового понятия понятие «четырехугольник», и выясните, являются ли прямоугольниками фигуры, изображенные на рисунке 12. Ответ обоснуйте.
212. Дайте определение прямоугольника, указав в качестве родового понятия понятие «параллелограмм», и выясните, являются ли прямоугольниками фигуры, изображенные на рисунке 13. Ответ обоснуйте.
213. Дайте определение квадрата, указав в качестве родового понятия понятие «прямоугольник», и выясните, какие из фигур, изображенных на рисунке 14, являются квадратами, а какие – нет. Ответ обоснуйте.
214. Дайте определение параллелограмма и выясните, какие из фигур, изображенных на рисунке 15, являются параллелограммами, а какие – нет. Ответ обоснуйте.
F2
Рис. 12
F2
Рис. 13
F3
F1
F2
 Рис. 14 Рис. 14

F2

F3

F1
Рис.15
215. Известно, что равносторонним является треугольник, у которого все стороны равны. Используя данное определение, выясните правильны ли следующие обоснования:
а) АВС – равносторонний, так как АВ = ВС.
б) ВЕР не является равносторонним, так как ВЕ ЕР.
216. Дайте определение трапеции и на его основе выясните, правильны ли следующие обоснования:
а) Четырехугольник АВСД – трапеция, так как ВС || АД и АВ СД.
б) Четырехугольник ЕFКLне является трапецией, так FК ЕL. Ответ обоснуйте.
217. Сформулируйте определение равнобедренного треугольника, указав в качестве видового отличия следующие свойства: «Хотябы две стороны треугольника равны», и выясните, правильны ли следующие обоснования:
а) треугольник АВС не является равнобедренным, так как АВ ВС.
б) треугольник DEFявляется равнобедренным, так как ЕF = FD. Ответ обоснуйте.
В задачах 159-161 выясните, правильно ли определены понятия, в случае же отрицательного ответа внесите соответствующие изменения в определение.
218. а) квадратом называется четырехугольник, укоторого все стороны равны;
б) именем прилагательным называется часть речи, обозначающая признак предмета и отвечающая на вопрос «какой»?
219. а) ромбом называется четырехугольник, у которого все стороны равны;
б) прямоугольником называется ромб с прямым углом.
220.а) биссектриса угла – это луч, делящий угол пополам;
б) равнобедренный треугольник – это треугольник, у которого хотя бы две стороны равны.
221. Дайте определение равнобочной трапеции, используя в качестве родового понятия: а) многоугольник; б) четырехугольник; в) трапецию.
222. В каждом из нижеприведенных умозаключений выделите посылки и заключение: а) Все студенты нашей группы ходили на экскурсию. Волкова учится в нашей группе. Значит, она ходила на экскурсию.
б) Все хвойные – вечнозеленые. Ель – хвойное дерево. Значит ель – вечнозеленая.
в) Каждый студент нашего факультета бывает в подшефном детском доме. Маша ни разу не была в этом детском доме. Следовательно, Маша не учится на нашем факультете.
г) Если натуральное число делится на 9, то оно делится на 3. Число 27 делится на 9, следовательно, число 27 делится на 3.
д) Всякое натуральное число – целое. Число 4, 5 не является целым, следовательно, оно не является натуральным.
223. Запишите логическую форму умозаключений, приведенных в № 221, и укажите те из них, которые построены по правилу:
а) отрицания; б) заключения; в) силлогизма.
224. Является ли данное рассуждение дедуктивным:
а) Если студент получил зачет по математике, он будет допущен к экзамену. Ребров не допущен к экзамену, следовательно, он не сдал зачет.
б) Все туристы оптимисты, Егор не турист, следовательно он не оптимист.
Запишите это умозаключение на теоретико-множественном языке.
225. Является ли данное рассуждение правильным: все числа, делящиеся на 9, делятся на 3. Число 105 не делится на 9. Значит, число 105 не делится на 3.
Все ромбы являются параллелограммами, четырехугольник а не ромб. Следовательно не является параллелограммом.
Все туристы – оптимисты. Сергей не оптимист, следовательно он не турист.
По теме данной главы студент должен уметь:
формулировать определения высказывания и предиката;
определять истинностные значения высказываний и находить множества истинности предикатов;
строить отрицание высказываний с кванторами;
выделять отношения рода и вида между понятиями, изучаемыми в начальной школе ;
раскрыть смысл понятия «отношение следования между предложениями» и приводить примеры таких отношений;
приводить примеры задач из учебников математики начальной школы, формирующие у учащихся представления об объеме и содержании понятий;
строить правильные умозаключения;
III. СООТВЕТСТВИЯ И ОТНОШЕНИЯ
Литература [1] гл. II §§ 8, 9, 10
СООТВЕТСТВИЯ МЕЖДУ ЭЛЕМЕНТАМИ ДВУХ МНОЖЕСТВ.
__________________________________________________________________
Определение 1. Соответствием Р между элементами множеств X и Y называется подмножество декартова произведения множеств X и Y, (Р XY)
_____________________________________________________________________________________________
Если элементу х из множества Х соответствует элемент у из множества У, то пишут хРу или (х,у)Р. Элемент уУ называется образом элемента х, а элемент хХ называют прообразом элемента уУ
Из определения следует, что соответствия можно задать: перечислением пар или графом (если множества конечные), указанием характеристического свойства элементов этого соответствия, графиком, если множества числовые, и табличным способом.
Пример 1.
П    усть Х = 2,6,8 ; У = 7,5,3,1 хРу усть Х = 2,6,8 ; У = 7,5,3,1 хРу  х < у х < у
З  ададим соответствие Р различными способами. ададим соответствие Р различными способами.
1. Перечислением пар: Р = (2,7),(2,5),(2,3),(6,7)
2. Графом. Граф – это ориентированный чертеж, состоящий из точек и стрелок, где точки изображают элементы множеств, а стрелки соединяют элементы множества Х с соответствующими элементами множества У.
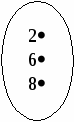  Х У Х У
3. График заданного соответствия выглядит так:
у
    7 7
 5 5
 3 3
1
 х х
1 2 6 8
4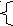  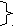 . Задаем данное соответствие с помощью характеристического свойства: . Задаем данное соответствие с помощью характеристического свойства:
Р = (х,у) х Х; у У, х у
__________________________________________________________________
Определение 2. Соответствие между элементами множеств Х и Y называют взаимно-однозначным, если любому элементу х X ставится в соответствие единственный элемент уY, и, наоборот, любой элемент у Y имеет единственный прообраз хХ в этом соответствии.
_____________________________________________________________________________________________
Пример 2.
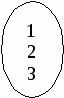 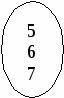 Х У Х У
Х    У У
Пусть х = {1,2, 3); у = {5, 6, 7}. х р у у= х + 4
__________________________________________________________________
Определение 3. Если между элементами множеств Х и Y можно установить каким-либо образом взаимно-однозначное соответствие, то говорят, что множества X и Y равномощны и пишут Х
Y. По определению, получим
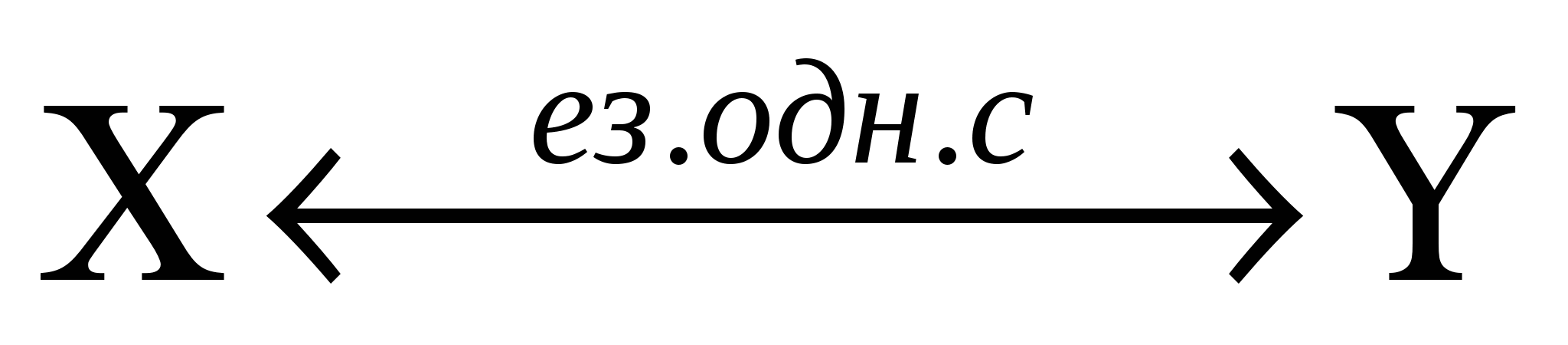   Y Y
_____________________________________________________________________________________________
__________________________________________________________________
Определение 4. Если множество А равномощно множеству натуральных чисел, то его называют счетным. А  N, А – счетное множество. N, А – счетное множество.
____________________________________________________________________________________
|
|
|
 Скачать 7.87 Mb.
Скачать 7.87 Mb.