Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы

• Название: Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
• Анкор: Praktikum_po_mat.doc
• Дата: 02.05.2017
• Размер: 7.87 Mb.
• Имя файла: Praktikum_po_mat.doc
• Тип: Контрольные вопросы; #6276
• страница: 16 из 19

Теорема 1. Одно и то же множество А не может быть взаимно од­нозначно отображено на два различных отрезка натурального ряда чисел.

Взаимно однозначное отображение множества А на отрезок N_a можно понимать как нумерацию элементов множества А: А N_a

Этот процесс нумерации называют СЧЕТОМ.

При пересчете элементы конечного множества А не только расставляются в определенном порядке (при этом используются порядковые натуральные числа, выражаемые числительными «первый» «второй», «третий» и так далее), но и устанавливается также, сколько элементов содержит множество А (при этом используются количес­твенные натуральные числа, выражаемые числительными «один» «два», «три» и так далее.).

Тесная связь порядкового и количественного натурального числа нашла отражение и в начальном обучении математике. С этими чис­лами учащиеся знакомятся уже при изучении чисел первого десятка. Происходит это при счете элементов различных множеств.

Задача 1.

Объясните смысл равенств: п(А) = 3; n(B) = 0. Приведите примеры множеств А и В, удовлетворяющих этим условиям.

Решение.

n(A) = 3 – число элементов (количество элементов) множества А равно трем. В качестве множества А можно взять множество сторон треугольника, углов треугольника, высот треугольника, п(В)=0 – чис­ло (количество) элементов множества В равно нулю, В – пустое мно­жество. Например, В – множество действительных решений уравнения х² +1 = 0.

Задача 2.

Используя теоретико-множественную трактовку отношения «меньше», покажите, что 3 < 5.

Решение.

Возьмем множество А, содержащее 3 элемента, и множество В, содержащее 5 элементов. Например, А – множество квадратиков, п(А)=3; В – множество кружков, п(В)=5. Из множества В можно выделить подмножество В₁, равномощное множеству А. Согласно определению отношения «меньше», последнее означает АВ₁BB₁  B B₁  , а это значит 3 < 5.
Контрольные вопросы

1. 
   Сформулируйте определение натурального числа.
   
2. 
   Сформулируйте определение отношения «равенства» на множестве натуральных чисел.
   
3. 
   Сформулируйте определение отношения «меньше» на множестве натуральных чисел.
   
4. 
   Сформулируйте свойства отношения «равенства» на множестве натуральных чисел.
   
5. 
   Сформулируйте свойства отношения «меньше» на множестве натуральных чисел.
   
6. 
   Дайте определение отрезка натурального ряда чисел и запишите множества N₃, N₆.
   
7. 
   Что значит сосчитать элементы конечного множества? Сформулируйте условия, которые должны соблюдать учащиеся, ведя счет предметов.
   
8. 
   Почему на урок, где изучается число «три», можно принести картинку с изображением трех яблок, трех карандашей и трех тетрадей, а можно ли воспользоваться и другими примерами трехэлементных множеств?
   

Упражнения

351. Докажите, что отношение «равенства» на множестве натуральных чисел является отношением эквивалентности.

352. Докажите, что отношение «меньше» на множестве натуральных чисел является отношением строгого линейного порядка.

353. Дайте теоретико-множественную трактовку отношения порядка «больше». Каков теоретико-множественный смысл свойства транзитивности этого отношения?

354. Прочитайте предложения: п(А) = 4; п(В) = 1. Приведите примеры множеств А и В, удовлетворяющих этим условиям.

355. Придумайте примеры множеств С и D, для которых выполняются условия: а) n(С) = n(D) и С D; б) n(С) = п(D) и С =D.

356. Используя теоретико-множественную трактовку отношения «меньше», покажите, что:

а) 4 < 7; б) 1 < 3.

357. Сравните числа п(А) и п(В), если: а) А B; б) AB и AB Приведите примеры множеств А и В, удовлетворяющих этим условиям.

358. Из учебников математики первого класса приведите примеры заданий, в которых отношение «меньше» («больше») на множестве натуральных чисел рассматривается с теоретико-множественных позиций.

359. 
     Приведите примеры заданий из учебников математики для начальных классов, в которых число выступает как характеристика: а) порядка; б) количества.
     
360. 
     Можно ли назвать отрезком натурального ряда множества: А, В, С, Д ?
     

а) А = {1,3,5,6,7};

b) В = {2,3,4,5};

с) С = {1,2, 3,4,5, 6,7};

d) D = {0, 1,2,3}.

Что значит сосчитать элементы множества? Осуществите счет для множеств А, В, С, D.

361. Сформулируйте условия, которые должны соблюдать учащиеся, ведя счет предметов.
2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ.
Пусть а = п(А); b= п(В).

Определение 16. Суммой чисел а и b называют количество эле­ментов в объединении непересекающихся множеств А и В. а + b = п(А В), если А  В = .
Так как А  В = , то п(А В)= п(А) + п(В)

(для любых множеств А и В п(А В) = п(А) + п(В) – n(А  В)).

Теорема. Сумма двух любых целых неотрицательных чисел всегда существует и определена однозначно.

______________________________________________________________________

Определение 6. Операция по нахождению суммы целых неотри­цательных чисел называется операцией сложения.

___________________________________________________________________________________________________
Свойства операции сложения

1. 
   ( а, b N₀) а + b = b + а (коммутативность).
   
2. 
   ( а, b, cN₀) (а + b) + c = a + (b +c) = а + b+ с (ассоциативность).
   
3. 
   ( а, b, cN₀)(а + b = а + с b = с)  (а + b = с + b а = с) (сократимость).
   
4. 
   ( а, b, cN)(а + b < а + с b < с)  (а + b < с + b а < с) (моно­тонность).
   
5. 
   ( а, bN)а + b а a + bb(сумма двух любых натуральных чисел не равна ни одному из слагаемых).
   
6. 
   ( а, bN)а + b > а a + b > b(сумма двух любых натуральных чисел больше любого из слагаемых)
   

Пусть а = п(А); b= п(В).

______________________________________________________________________

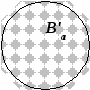
Определение 7.Разностью чисел а и b называется количество элементов разности множеств А и В при условии В  А.

___________________________________________________________________________________________________

a – b = п (А\В), если В  А или а – b = п(В'_А).

А



______________________________________________________________________

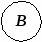
Определение 8. Разностью чисел а и b называют число с, если оно существует, такое, что а = b + с, а – в = с а = в + с

___________________________________________________________________________________________________

Эти определения равносильны. Действительно, пусть а = п(А); b= п(В); В  А, с = п(В'_А). В'_А = А\В, если В А, А = В  В'_А, причем В В'_А =, п(А) = п(В  В'_А) = п(В) + п(В'_А), т.е. а = b + с.

______________________________________________________________________

Определение 9. Операция по нахождению разности целых не­отрицательных чисел называется операцией вычитания.

___________________________________________________________________________________________________
Разность чисел а и bсуществует, когда а b.
Задача 3.

1. 
   Доказать свойство ассоциативности операции сложения.
   
2. 
   Дать теоретико-множественное истолкование правила вычита­ния числа из суммы.
   

Решение. 1. Докажем, что ( а, b, cN)(а + b) + с = a + (b + с).

Дадим теоретико-множественное истолкование числовых выра­жений, записанных в левой и правой частях этого числового раве­нства. Пусть

а = п(А); b = п(В); с = п(С); тогда а + b = п(А В), если А В = , (а + b) + с = п((А  В) С), если (А В)  С = ,

b + с = п(В C), если В  С = , а +(b + с) = п(А  (В  С)), если А  (ВС) = .

И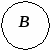спользуя диаграммы Эйлера-Венна, множества А, В и С можно изобразить так:


Пользуясь свойством ассоциативности операции объединения множеств, получаем

(A,B, С) (A B) C = А  (В  С)  п((АB) С) = п(А (ВС))  (а +b) + с = а + (b + с)

(равные множества имеют и равное число элементов).

2. Рассмотрим один из способов вычитания, например (а + b)–с =(а – с)+b, если а>с. Пусть а = п(А); b= п(В); с = п(С). Дадим теоре­тико-множественное истолкование числовых выражений, запи­санных в левой и правой частях этого числового равенства. Для левой части равенства получим:

а + b = п(А  В), если А B = ,

(а + b) – с = п((А В)\С), если С  А  В.

Используя диаграммы Эйлера-Венна, множества А и В можно изобразить так:


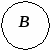
Множество С может быть подмножеством А или В. Рассмотрим случай, когда С  А.

В правой части равенства получим:

а – с = п(А\C, т.к. С  А, (а – с) + b = п((А\С)  В), если (А\С) B = .
В этом случае множества изображаются так:

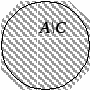В

В левой части равенства круг для множества С расположен внутри круга для множества А.

Можно доказать, что (А  В) \ С = (А \ С)  В. Так как равные множества имеют равное число элементов, получаем:

п((А В)\С) = п((А \С)  В) => (а + b) – с = (а – с) + b.

Задача 4.

Решить задачу и обосновать выбор действий.

1. 
   Оля собрала грибы: два белых и пять подосиновиков. Сколько грибов собрала Оля?
   
2. 
   У Тани пять шариков, два из них она отдала Лене. Сколько шариков осталось у Тани?
   

Решение.

Переведем условие и вопрос задач на язык теории множеств.

1. Пусть А – множество белых грибов, которые собрала Оля, по условию задачи п(А) = 2;

В – множество подосиновиков, которые собрала Оля, по условию задачи п(В)=5;

С – множество всех грибов, которые собрала Оля. Число элементов множества С неизвестно, его надо найти, т.е. п(С) – ?


C






A B

Множество С являетсяобъединением множеств А и В; С = А В, причем А B = .

n (C) = п(А  В) = п(А) + п(В) = 2 + 5 = 7.

Оля собрала 7 грибов.

Эта задача на уяснение конкретного смысла сложения натураль­ных чисел.

2. Пусть А – множество шариков, которые были у Тани, по условию задачи п(А) = 5;

В – множество шариков, которые Таня отдала Лене, по условию задачи п(В)=2;

С – множество шариков, которые остались у Тани, численность множества С неизвестна, ее надо найти, т.е. п(С) – ?

Выразим множество С через множества А и В.

А




С В

А = В С, В С = 

С – разность множеств А и В, причем В  А. С = А\В, тогда n(C) = п(А \ В) = п(А) – п(В) = 5 – 2 = 3, т.е. n(С) = 3.

У Тани осталось три шарика.

Эта задача на уяснение смысла действия вычитания натуральных чисел.
Задача 5

Решить и обосновать выбор действий.

1. 
   У Кати было 3 шара, а у Тани на 1 шар больше. Сколько шаров было у Тани?
   
2. 
   В парке 7 берез, а елей на 2 меньше. Сколько елей в парке?
   
3. 
   На верхней полке 9 книг, а на нижней 5. На сколько книг больше на верхней полке, чем на нижней?
   

Решение.

Переведем условие и вопрос задач на язык теории множеств.

1. Пусть А – множество шаров у Кати, по условию задачи п(А)=3; В – множество шаров у Тани, число их неизвестно, т.е. п(В) – ? У Тани на 1 шар больше, чем у Кати, это значит, что у Тани ша­ров столько же, сколько у Кати, и еще один. Введем в рассмотрение вспомогательные множества: В₁ – множество шаров у Тани, которых было столько же, сколько у Кати, т.е. В₁ А и тогда n(B₁) = п(А)= 3; В₂ – множество шаров у Тани, которых у Кати нет. По условию задачи п(В₂) = 1, т.к. у Тани на 1 шар больше.

Изобразим схематически множества и выразим множество В че­рез вспомогательные множества.

А –

В –



В₁ В₂

В – объединение множеств B₁ и В₂, причем В₁ В₂ = , В = В₁и В₂, тогда п(В) = п(В₁) + п(В₂) = 3 + 1 = 4.

У Тани было 4 шара.

Эта задача на смысл отношения «больше на...».

2. Пусть А – множество берез в парке, число их равно 7, т.е. п(А) = 7;

В – множество елей в парке, число их надо найти, т.е. п(В) – ?

Елей на три меньше, чем берез, т.е. елей столько же, сколько бе­рез, но без трех. Введем в рассмотрение вспомогательные мно­жества:

B₁– множество елей в парке, которых было бы столько же, сколько берез, т.е. В₁ А, и тогда n(B₁) = п(А) = 7.

В₂ – множество елей, которых в парке нет, т.к. их на 3 меньше, чем берез то п(В₂) = 3, причем В₂B₂.

Изобразим схематически множества и выразим множество В через вспомогательные множества.



А –




В₁ –



В В₂

В – разность множеств В₁и В₂, причем В₂ В₁, т.е. В = В₁\ В₂, тог­да п(В) = п(В₁\В₂) = п(В₁) – п(В₂) = 7 – 3 = 4.

В парке 4 ели.

Эта задача на смысл отношения «меньше на...».

3. Пусть А – множество книг на верхней полке, число их равно 9, т.е. п(А) = 9;

В – множество книг на нижней полке, число их равно 5, т.е. п(В) = 5;

Введем в рассмотрение вспомогательные множества:

А₁ – множество книг на верхней полке, в котором их столько же, сколько на нижней, т.е. A₁ B, и тогда п(А₁) = п(В)= 5;

А₂ – множество книг на верхней полке, которых нет в А₁. Число элементов множества А₂надо найти, т.е. п(А₂) – ?

Изобразим схематически множества и выразим множество А₂через другие множества.

А –



А₁ А₂
В –
А₂ – разность множеств А и А₁, причем А₁ А;

А₂ = А\А₁, тогда п(А₂) = п(А\А₁) = п(А) – п(А₁) = 9 – 5 = 4.

На верхней полке на четыре книги больше, чем на нижней.