Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
 Скачать 7.87 Mb. Скачать 7.87 Mb.
|
На рисунке А\В заштриховано.Например, А = {1, 2, 3, 4}; В = {3, 4, 5, 6}, А\В = {х/х А и х В} = {1,2}, В\А= {х/х В и х А} = {5,6}. Очевидно, что х А\В тогда и только тогда, когда х А или х (А В). Для любых множеств А, В и С справедливы следующие равенства, связывающие вычитание множеств с другими операциями над множествами: а) А\(В С) = (А\В) (А\С); б) А\(В С)= (А\В) (А\С). ____________________________________________________________ Определение 8. Если В подмножество А, то разность А\В называют дополнением к подмножеству В и обозначают В'А. _________________________________________________________________________________________ Таким образом, В А, А\В = В'А .   На рисунке множество В'Азаштриховано. Так, если А – множество учащихся в некотором классе, а В – множество девочек в нем, то В'А есть множество мальчиков в этом классе. Если для множеств А, В, ... фиксировано некоторое универсальное множество И, то вместо А'и , В'ипишут А', В',... Очевидно, что х А', тогда и только тогда, когда х А или х И. Для любых подмножеств А и В универсального множества И имеют место следующие равенства:
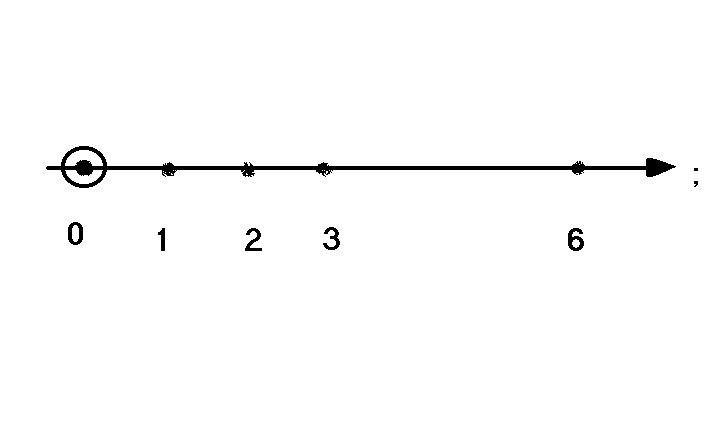
Задача 1 1. Множество А – множество натуральных делителей числа 6. Задать множество: а) перечислением элементов, б) графически, в) с помощью характеристического свойства. 2. Изобразить множество В = {х/х R, 1 х < 3, 5} на числовой прямой. Решение. 1. Множество А задано словесно – множество натуральных делителей числа 6, т.е. множество натуральных чисел, на которые число 6 делится без остатка (6 а) А = {1, 2, 3, 6};
в)А = {х/х N, 6 2. Множество В задано с помощью характеристического свойства. Перейти к заданию множества В в виде промежутка и изобразить на числовой прямой.
Задача 2. Проиллюстрируйте с помощью диаграмм Эйлера высказывания: а) некоторые нечетные натуральные числа кратны 5; б) все студенты нашего курса присутствовали на лекции по математике. Решение. Выделим множества, о которых идет речь в данных высказываниях: а) пусть А – множество нечетных натуральных чисел, В – множество натуральных чисел, кратных 5. В данном высказывании говорится, что некоторые элементы множества А являются и элементами множества В (например, 5, 15), т.е. множества А и В имеют общие элементы. Но в каждом множестве есть элементы, не принадлежащие другому. Поэтому круги для множеств А и В надо изобразить так, чтобы они пересекались друг с другом (рис. 4).  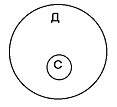 Рис.4 Рис.5 б) Пусть D– множество студентов курса, C – множество студентов, присутствовавших на лекции по математике. В данном высказывании утверждается, что каждый элемент множества С является и элементом множества Д (все элементы множества С принадлежат множеству Д). По определению отношения включения, это означает, что С Д. Поэтому круг для множества С расположен внутри круга для множества Д (рис. 5). |