Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
 Скачать 7.87 Mb. Скачать 7.87 Mb.
|
|
5. РАЗБИЕНИЕ МНОЖЕСТВА НА КЛАССЫ Можно говорить о разбиении данного множества на попарно непересекающиеся подмножества или классы тогда, когда одновременно выполняются следующие условия:
Символическая запись этого определения следующая. Пусть дано множество А и совокупность его подмножеств: А1, А2, ..., Ап (где Аi А, i = 1, 2,..., n). Совокупность подмножеств А1, А2, ..., Ап называется разбиением множества А на классы, а сами подмножества – классами, если выполняются условия:
Рассмотрим задачи, связанные с оценкой правильности разбиения множества на классы и с самостоятельным разбиением множества на классы при использовании двух свойств. Задача 7 Учащийся из множества четырехугольников выделил подмножества трапеций, параллелограммов и прямоугольников. Произошло ли разбиение множества на классы? Решение. Пусть А – множество четырехугольников. А1 – множество трапеций А2 – множество параллелограммов, А3 – множество прямоугольников. Разбиение множества А на классы произойдет, если будут выполнены условия (1, 2, 3). Проверим выполнимость условий: Аi А, где i = 1, 2, 3. 1. Аi, где i = 1, 2, 3, т.к. каждое множество содержит хотя бы по oдной фигуре. 2. А1А2 = ; А1А3 = ; А2 А3, т.к. А3 А2 и А2А3=А3. Второе условие не выполняется, значит разбиения множества на классы не произошло. Задача 8 На какие классы разбивается множество натуральных чисел, если использовать такие свойства: «делится на 2» и «быть однозначным»? Решение. Обозначим через А множество четных натуральных чисел, В – множество однозначных чисел, N–множество натуральных чисел. Заметим, то А В , т.к. некоторые четные числа являются однозначными, а некоторые однозначные числа – четными. Далее с помощью кругов Эйлера изобразим множества А, В, Nи выделим классы разбиения. Из рисунка видим, что их 4. Охарактеризуем каждый из них. 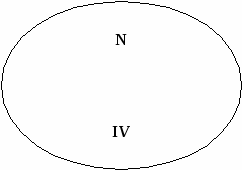 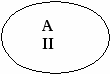 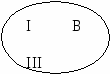 I – множество четных однозначных натуральных чисел. II – множество четных неоднозначных натуральных чисел. III – множество нечетных однозначных натуральных чисел. IV – множество нечетных неоднозначных натуральных чисел. Упражнения 93. Из множества Р = {1, 2, 3, 4, 5, 6, 7, 8, 9} выделили подмножества А, В и С. Выясните, в каком случае произошло разбиение множества Р на классы: а) А = {1, 3, 5}, В = {2, 4, 6, 8}, С = {7, 9}; б) А = {5}, В = {3, 4, 8, 9}, С = {1, 6}; в) А = {1, 3, 5), В = {2, 4, 6, 8}, С = {5, 7, 9}; г) А = {1, 3}, В = {4, 6, 8}, С = {5, 6, 9}. 94. Множество А состоит из 3, 4, 5, 6, 7, 8, 9; множество В – его подмножество, состоящее из чисел, которые делятся на 3; множество С – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 1; множество D – подмножество, состоящее из чисел, которые при делении на 3 дают в остатке 2. Можно ли утверждать, что множество А разбивается в этом случае на попарно непересекающиеся подмножества В, С и D? Произошло ли разбиение множества на классы, если да, то сколько классов? 95. На координатной прямой выделены два множества: (– 96. Выясните, в каких случаях классификация выполнена верно: а) треугольники делятся на прямоугольные, тупоугольные и равнобедренные; б) углы классифицируются на острые, прямые и развернутые; в) целые числа можно разбить на натуральные числа, число 0 и отрицательные целые числа; г) глаголы русского языка делятся на глаголы настоящего, прошедшего и будущего времени; д) члены предложения бывают главные и второстепенные. 97. Из множества Т треугольников выделили два подмножества: X– подмножество прямоугольных треугольников и Y – подмножество равнобедренных треугольников. Постройте для данных множеств круги Эйлера; установите, на сколько непересекающихся областей разбился круг, изображающий множество Т, и все множества, изображенные этими областями, задайте описанием характеристического свойства. При помощи скольких свойств произведено разбиение множества треугольников на классы? 98. Разбейте множество четырехугольников на классы: а) по какому-либо одному свойству; б) по двум свойствам. Укажите эти свойства, для каждого случая постройте круги Эйлера, установите число непересекающихся областей и выясните, какие множества изображаются этими областями. 99. Множества Р ромбов, Т треугольников и К многоугольников, имеющих угол 30°, являются подмножествами множества М многоугольников. Постройте круги Эйлера для данных множеств, установите, на сколько непересекающихся областей разбился круг, изображающий множество М, и для всех множеств, изображенных этими областями, укажите характеристическое свойство. 100. Из множества треугольников выделены подмножества прямоугольных, равнобедренных и тупоугольных треугольников. Произошло ли разбиение множества на классы? 101. Произведите разбиение на классы множества целых чисел, используя свойства «быть кратным 4» и «быть кратным 5». 102. Укажите классы разбиения множества треугольников, которые получаются при рассмотрении таких свойств, как «иметь хотя две равные стороны» и «иметь прямой угол». 103. Из множества четырехугольников выделили следующие подмножества: а) прямоугольников, не являющихся ромбами; б) ромбов не являющихся прямоугольниками; в) квадратов; г) четырехугольников, не являющихся ни ромбами, ни прямоугольника. Произошло ли разбиение множества на классы? 104. Истинно ли высказывание: «Параллелограммы делятся на прямоугольники, ромбы и квадраты»? Почему? 105. На множестве геометрических фигур плоскости выделены множества фигур, имеющих: а) центр симметрии; б) ось симметрии; в) не имеющих ни центра, ни оси симметрии. Можно ли считать, что произошло разбиение множества на классы? 106. Произведите разбиение множества целых чисел на классы используя такие свойства: «быть однозначным числом» и «быть двузначным числом». 107. Укажите, какие классы разбиения получаются при рассмотрении на множестве треугольников таких свойств: «иметь тупой угол» и «все углы острые». 108. Произошло ли разбиение множества натуральных чисел на классы, если из него выделены подмножества чисел, делящихся на три чисел, которые при делении на 3 дают остаток 1? 109. Установите, правильны ли следующие классификации: а) натуральные числа делятся на однозначные, двузначные и трехзначные; б) параллелограммы могут быть прямоугольниками, квадратами и ромбами; в) треугольники бывают равносторонними и неравносторонними; г) четырехугольники делятся на параллелограммы и трапеции. 110. Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 4. Постройте круги Эйлера для множеств N, А и В; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N; укажите характеристические свойства этих множеств. 111. Из множества параллелограммов выделили подмножество прямоугольников и подмножество квадратов. Постройте круги Эйлера для данных множеств. Можно ли утверждать в данном случае, что множество параллелограммов разбито на 3 попарно непересекающихся подмножества: квадраты; прямоугольники, не являющиеся квадратами; параллелограммы, не являющиеся прямоугольниками? 6. ДЕКАРТОВО УМНОЖЕНИЕ МНОЖЕСТВ Назовем (х, у) упорядоченной парой, а х и у – компонентами этой пары. При этом считают, что (х1 у1) = (х2.у2), если х1 = х2 и у1= у2. __________________________________________________________________ Определение 9. Декартовым произведением множеств А и В называют множество АВ, элементами которого являются все пары(х,у), такие, что х А, уВ, т.е. АВ = {(х,у)/х А, у В}. _____________________________________________________________________________________________ Найдем, например, декартово произведение множеств А = {1,3} и В ={2,4,6}. АВ = {(1, 2);(1, 4);(1, 6);(3, 2);(3, 4);(3, 6)}. Операцию, при помощи которой находят декартово произведение, называют декартовым умножением множеств. Декартово умножение множеств не обладает ни свойством коммутативности, ни свойством ассоциативности, но связано с операциями объединения и вычитания множеств дистрибутивными свойствами: для любых множеств А, В, С имеют место равенства: (А В) С = (АС) (ВС), (А\В)С = (АС)\(ВС). Для наглядного представления декартова произведения числовых множеств часто используют прямоугольную систему координат. Пусть А и В – числовые множества. Тогда элементами декартова произведения этих множеств будут упорядоченные пары чисел. Изобразив каждую пару чисел точкой на координатной плоскости, получим фигуру, которая и будет наглядно представлять декартово произведение множеств А и В. Изобразим на координатной плоскости декартово произведение множеств А и В, если: a) A= {2, 6}; B ={1,4}, б) А = {2, 6}; В = [1,4], в) А = [2, 6]; B =[1,4]. В случае а) данные множества конечны и можно перечислить элементы декартова произведения. АВ = {(2, 1); (2, 4); (6, 1); (6, 4)}. Построим оси координат и на оси ОХ отметим элементы множества А, а на оси ОУ – элементы множества В. Затем изобразим каждую пару чисел множества АВ точкам на координатной плоскости (рис.7). Полученная фигура из четыре точек и будет наглядно представлять декартово произведение данных множеств А и В. В случае б) перечислить все элементы декартова произведения множеств невозможно, т.к. множество В – бесконечное, но можно представить процесс образования этого декартова произведения: в каждой паре первая компонента либо 2, либо 6, а вторая компонента – действительное число из промежутка [1,4]. Все пары, первая компонента которых есть число 2, а вторая пробегает значение от 1 до 4 включительно, изображаются точками отрезка СД, а пары, первая компонента которых есть число 6, а вторая – любое действительное число из промежутка [1,4], – точками отрезка РS(рис.8). Таким образом, в случае б) декартово произведение множеств А и В на координатной плоскости изображается в виде отрезка СД и РS. 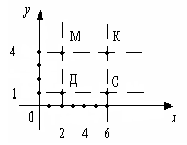 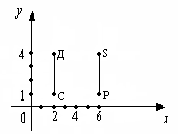 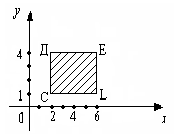 Рис. 7 Рис. 8 Рис. 9 Случай в) отличается от случая б) тем, что здесь бесконечно не только множество В, но и множество А, поэтому,первой компонентой пар, принадлежащих множеству А В, является любое число из промежутка [2, 6]. Точки, изображающие элементы декартова произведения множеств А и В, образуют квадрат СДЕL(рис. 9). Чтобы подчеркнуть, что элементы декартова произведения изображаются точками квадрата, его можно заштриховать. Контрольные вопросы
а) Запишите все дроби, числителем которых является число из множества А = {3, 4}, а знаменателем – число из множества В = {5, 6, 7}. б) Запишите различные двузначные числа, используя числа 1, 2, 3, 4.
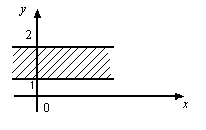 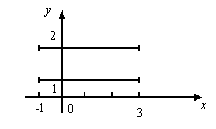  а) б) в) Рис. 10 Упражнения 112. Запишите все двузначные числа, цифры десятков которых принадлежат множеству А = {1, 3, 5}, а цифры единиц – множеству В = {2,4,6}. 113. Напишите все дроби, числители которых выбираются из множества А= {3, 5, 7}, а знаменатель – из множества В= {4, 6, 8}. 114. Напишите все правильные дроби, числители которых выбираются из множества А = {3, 5,7}, а знаменатель – из множества В= {4, 6,8}. 115. Даны множества Р = {1, 2, 3}, К= {а, b}. Найдите все декартова произведения множеств Р К иKР. 116.Известно, что АВ = {(1, 2); (3, 2); (1, 4);(3, 4); (1, 6); (3, 6)}. Установите, из каких элементов состоят множества А и В. 117.Запишите множества (АВ)С и А(ВС) перечислениемпар, если А={а, b}, B = {3},C={4, 6} 118. Составьте множества АВ, ВА, если: a)А = {а,b,с},В={d}, б) A = {a, b}, B = , в) А= {т, п, k }, В = А, г)A = {x, y, z}, B = {k, n} 119. Известно, что АВ = {(2,3), (2,5), (2,6), (3,3), (3,5), (3,6)}. Установите, из каких элементов состоят множества А и В. 120. Найдите декартово произведение множеств А = {5, 9, 4} и В = {7, 8, 6} и выделите из него подмножество пар, в которых: а) первая компонента больше второй; б) первая компонента равна 5; в) вторая компонента равна 7. 121. Перечислите элементы, принадлежащие декартову произведению множеств А, В и С, если: а) А = {2, 3}, В = (7, 8, 9}, С = {1, 0}; б) А = В = С = {2, 3}; в) А = {2, 3}, B= {7, 8, 9}, С = 122. Изобразите на координатной плоскости элементы декартова про изведения множеств А и В, если: а) А = {х/х N, 2 < х < 4}, В = {х/хN, х < 3}; б) А = {х/х R, 2 < х < 4}, В = {х/х N, х < 3}; в) А = [2, 4]; В = [1,2]. 123. Все элементы декартова произведения двух множеств A и B изображены точками в прямоугольной системе координат. Запишите множества A и В (рис. 11).    а) б) в) Рис. 13 124. Изобразите на координатной плоскости элементы декартова произведения множеств X и Y, если: а) Х={–1,0, 1,2}, Y={2, 3,4}; б) Х={–1,0, 1,2}, Y=[2, 4]; в) Х = [–1;2], Y = {2, 3, 4}; г) Х = [1;7], Y = [2; 6]; д) X = [–3; 2], Y = [0; 5[; е) X = R, Y= [–2; 2]; ж) Х= ]–3;2[, Y=R; з) Х={2}, Y=R; и) Х= R, Y = {–3}. 125. Фигуры, приведенные на рис. 14, являются результатом изображения на координатной плоскости декартова произведения множеств X и Y. Укажите для каждой фигуры эти множества.    а) б) в)   г) д) Рис. 14 126. Выясните, декартово произведение каких двух множеств изображается на координатной плоскости в виде полуплоскости. Рассмотрите все случаи. 127. Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде прямого угла, который образуется при пересечении координатных осей. 128. На координатной плоскости постройте прямую, параллельную оси ОХ и проходящую через точку Р (–2, 3). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой. 129. На координатной плоскости постройте прямую, параллельную оси ОY и проходящую через точку Р (–2, 3). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой. 130. На координатной плоскости постройте полосу, ограниченную прямыми, проходящими через точки (–2, 0) и (2, 0) и параллельными оси ОY. Опишите множество точек, принадлежащих этой полосе. 131. На координатной плоскости постройте прямоугольник, вершинами которого служат точки А (–3, 5), В (–3, 8), С (7, 5), D(7, 8). Опишите множество точек этого прямоугольника. 132. Постройте на координатной плоскости множество точек, координаты которых удовлетворяют условию: а) х R, у = 5; б) х = –3, у R; в) хR, |у| = 2; г) |x| = 3, у R; д) х R, y≥4; е) xR, y 4; ж) х R, |у| 4; з) |x| 4, |у| 3; и) |х| ≥1, |у| ≥ 4; к)|х| ≥ 2, у R. 133. На координатной плоскости изобразите элементы декартова произведения множеств XиY, если: а) X = R, Y = {3}; б) X = R, Y = [–3; 3]; в) X = [0; 134. На координатной плоскости постройте фигуру F, если а) F = {(х, у) |х = 2, у R} б) F = {(х, у) | xR, у = –3}; в) F = {(х, у) | х 2, у R}; г) F = {(х, у) | х К, y≥ – 3}; д) F = {(х, у) | |х| = 2, у R}; е) F={(х,у) |х R, |у| = 3}. 135. Постройте прямоугольник с вершинами в точках (–3, 4), (–3, –3), (1, –3), (1, 4). Укажите характеристическое свойство точек, принадлежащих этому прямоугольнику. 136. На координатной плоскости постройте прямые, параллельные оси ОХ и проходящие через точки (2, 3) и (2, –1). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде полосы, заключенной между построенными прямыми. 137. На координатной плоскости постройте прямые, параллельные оси ОY и проходящие через точки (2, 3) и (–2, 3). Установите, декартово произведение каких двух множеств изображается на координатной плоскости в виде полосы, заключенной между построенными прямыми. 138. Изобразите в прямоугольной системе координат множество XY, если: a)X = R; Y ={ yу R, |у| < 3}, б) Х= {x/xR, |х| > 2}; Y= {у/у R, |у| > 4}. |
