|
|
Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
Задача 6.
Решить и объяснить выбор действий.
В парке 9 кленов. Их на три больше, чем лип. Сколько лип в парке?
На столе 6 чашек, их на 2 меньше, чем ложек. Сколько ложек на столе?
Решение.
1. Первый способ. Пусть А – множество лип в парке, число их надо найти, т.е. п(А) – ? В – множество кленов в парке, число кленов равно 9, т.е. п(В) = 9. Кленов на три больше, чем лип, это значит, что кленов столько же, сколько лип, и еще три. Введем в рассмотрение вспомогательные множества:
B1 – множество кленов, которых столько же сколько было бы лип, тогда В1
А и n (B1) = п(А);
B2 – множество кленов из множества В, которые не вошли в В1, т.е. В2 В, В1 В2= и В =В1 В2, причем п(В2) = 3.
Надо найти п(А); п(А) = п(В1). Изобразим множества схематически и выразим множество В1через другие множества.
А –
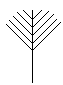
В – –

В1 В2
В1 – разность множеств В и В2, В1 = В \ В2, причем В2 В, тогда п(В1) = п(В\В2) = п(В) - п(В2) = 9 – 3 = 6, п(В1) = 6, тогда п(А) = 6. В парке 6 лип.
Второй способ. Пусть A – множество лип в парке, число их надо найти, т.е. п(А) – ? В – множество кленов в парке, число их равно 9, т.е. п(В) = 9. Так как кленов на три больше, чем лип, то лип на 3 меньше, чем кленов. Введем в рассмотрение вспомогательные множества:
А1 – множество лип, в котором лип было бы столько же, сколько кленов, т.е. А1
В и п(А1) = п(В) = 9;
А2 – множество лип из А1, которые не вошли в А, т.е. п(А2) = 3, А2 А1, А2А= , тогда A1 = А А2.
Изобразим схематически множества и выразим множество А через другие.
А1 –
 
А А2
В –
А – разность множеств А1и А2, А=А1\A2, причем, А2 А1, тогда п(А)= п(А1\А2) = п(А2) –п(А2)= 9 – 3 = 6.
В парке 6 лип.
2. Первый способ. Пусть А – множество чашек на столе, число чашек 6, т.е. п(А) = 6; В – множество ложек на столе, число ложек надо найти, т.е. п(В) – ? Чашек на 2 меньше, чем ложек, это значит чашек столько же, сколько ложек, но без 2. Введем в рассмотрение вспомогательные множества:
А1 – множество чашек, в котором чашек было бы столько же, сколько ложек, тогда А1
В и n(A1) = п(В);
А2 – множество чашек, которые не вошли во множество А, т.е. п(А2) = 2; А2 А1, А А2 = , причем A1 =А А2.
Надо найти п(В); п(В) = п(А1). Изобразим множества схематически и выразим множество А1через другие.
А1 –
 
А А2
В –
А1 – объединение множеств А и А2, причем А А2 =. А1=А А2, тогда п(А1) = п(А А2) = п(А) + п(А2)= 6 + 2 = 8. т.к. п(В) = п(А1), то восемь ложек на столе.
Второй способ. Пусть А – множество чашек на столе, число чашек 6, т.е. п(А) = 6; В – множество ложек на столе, число ложек надо найти, т.е. п(В) – ? Чашек на две меньше, чем ложек, тогда ложек на две больше, чем чашек. Введем в рассмотрение вспомогательные множества:
В1– множество ложек, в котором ложек столько же, сколько чашек, тогда В1
А и п(В1)= п(А) = 6;
В2 – множество ложек из В, которые не вошли в В1, т.е. п(В2) = 2, причем В1 В2=, В = В1и В2.
Изобразим схематически множества и выразим множество В через другие.
А –
В –
 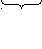
В1 В2
В – объединение множеств B1 и В2, В = В1 В2, причем В1B2 = , тогда п(В) = n(B1B2) = n(B1) + п(В2) = 6 + 2= 8. На столе 8 ложек.
Задача 7. Найти значение выражения и объяснить, какие свойства были при этом использованы: 53 + 119 + 47 + 31. Первый способ.Можно находить значение числового выражения в порядке выполнения действий, т.е.
53 + 119=172;
172 + 47 = 219;
219 + 31=250.
Второй способ.Можно найти значение этого выражения, используя свойства операции сложения. 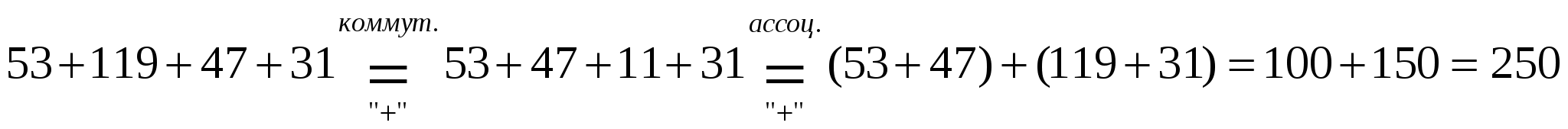 Контрольные вопросы Контрольные вопросы
Дайте теоретико-множественное истолкование суммы двух целых неотрицательных чисел. Объясните, почему сумму чисел связывают с объединением непересекающихся множеств, а не множеств вообще.
Запишите свойства операции сложения.
Дайте определение разности через дополнение подмножества и через сумму, докажите их равнозначность.
Запишите, используя символы, правила:
а) вычитания числа из суммы; б) вычитания суммы из числа; в) вычитания суммы из суммы. Приведите примеры на применение этих правил.
Запишите, используя символы, правила:
а) прибавления числа к сумме; б) прибавления суммы к числу; в) прибавления суммы к сумме. Приведите примеры на применение этих правил. Упражнения362. Докажите свойства операций сложения: а) коммутативность, б) ассоциативность.
Дайте теоретико-множественное истолкование свойств операции сложения:
а) сократимость, б) монотонность, в) 5-го и 6-го свойств.
Дайте теоретико-множественное истолкование нижеуказанных правил. Приведите примеры заданий из учебников математики начальных классов, при выполнении которых можно пользоваться этими правилами:
а) правило вычитания числа из суммы; б) правило вычитания суммы из числа; в) правило вычитания суммы из суммы; г) правило сложения суммы с суммой.
Запишите нижеуказанные правила. Дайте теоретическое обоснование им, каждый шаг обоснуйте:
а) правило сложения числа с суммой; б) правило сложения суммы с числом. Решить и объяснить выбор действий.
а) У Саши было 6 значков, а у Лены 4 значка. Сколько значков у Саши и у Лены вместе?
б) У Саши было 6 значков, 2 значка он отдал Лене. Сколько значков осталось у Саши?
а) Столяр сделал 8 книжных полок, а кухонных полок на 3 меньше. Сколько кухонных полок сделал столяр? Сколько всего полок сделал столяр?
б) На елке горели 10 зеленых лампочек, а красных на 4 меньше. Сколько красных лампочек на елке?
а) На елку повесили 7 красных шаров, а синих на три больше. Сколько всего шаров повесили на елку?
б) Сережа вырезал 5 красных флажков, а зеленых на 4 больше. Сколько всего флажков вырезал Сережа?
а) Для детского сада купили 10 кукол, 8 заводных машин, а мячей столько, сколько кукол и машин вместе. Сколько купили мячей? б) В одной вазе 5 апельсинов, в другой 7 апельсинов, а в третьей столько, сколько в первой и во второй вместе. Сколько апельсинов в третьей вазе?
а) У пристани стояли 3 теплохода и 9 катеров. На сколько меньше было теплоходов, чем катеров?
б) В одном ряду 5 кустов смородины, а в другом 11 кустов. На сколько кустов смородины больше во втором ряду, чем в первом?
а) В школьном саду 7 яблонь, это на 3 больше, чем груш. Сколько всего яблонь и груш в саду?
б) В букете было 4 красных пиона, их на 1 больше, чем розовых. Сколько всего пионов было в букете?
а) Дети играли в слова. Катя написала 8 слов, это на 5 меньше, чем написала Ира. Сколько всего слов написали девочки?
б) В саду посадили саженцы. Вишен 4, их на три меньше, чем слив. Сколько всего саженцев посадили в саду?
а) У Жени было 20 открыток. 4 открытки она отдала для школьной стенгазеты, 3 открытки подарила подруге. Сколько открыток осталось у Жени?
б) В трамвае ехали 42 человека. На остановке вышли 8 человек, а вошли 12 человек. Сколько человек стало в трамвае?
а) Нина нашла 32 желудя, Катя на 6 желудей больше, чем Нина, а Оля на 9 желудей меньше, чем Катя. Сколько желудей нашла Оля?
б) Юннаты на первую грядку посадили 40 кустиков клубники, да вторую на 6 кустиков меньше, чем на первую, а на третью на 10 кустиков больше, чем на вторую. Сколько кустиков клубники юннаты высадили на третью грядку?
Вычислить рациональным способом, объяснить вычисления.
а) 209 + 66 + 91+34 + 72;
б) 57 + 68 + 89 + 32+11+43;
в) 38+ 89+ 32+11;
г) (251 + 37) + (63+ 49);
д) (368 + 81) + (32 + 119);
е)179 – (39 +120);
ж)157 – (29 + 27);
з) (173 + 34) – (53+ 24);
и) 203 + 69 + 97 + 31+ 93;
к) 157 +178 + 74 + 43 +22.
3. УМНОЖЕНИЕ ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫЙ ЧИСЕЛ______________________________________________________________________ Определение 10. Операция нахождения произведения целых неотрицательных чисел называется операцией умножения.___________________________________________________________________________________________________ Теоретико-множественное определение произведения. Пусть а = п(А), b = п(В).______________________________________________________________________ Определение 11. Произведением чисел а и b называют число элементов декартова произведения множеств А и В.___________________________________________________________________________________________________ Символическая запись: а b= п (А В). Имеет место теорема. Теорема 2. Произведение двух любых целых неотрицательных чисел всегда существует и определенно однозначно. Свойства операции умножения
( а, b N0) а b = b а (коммутативности);
( а, b,c N0) а (bc)= (а b)c= abc(ассоциативности);
( а, b,c N0) а b = acb = c а b= cba = c(сократимости);
( а, b,c N) а b < acb < c а b< cba < c(монотонности);
Свойства дистрибутивности операции умножения относительно сложения слева и справа:
( а, b,c N) а ( b + c) ab +ac; ( а, b,c N) (а + b) c = ac +bc; 6. Свойства дистрибутивности операции умножения относительно вычитания слева и справа: ( а, b,c N) а ( b – c)= ab – ac; ( а, b,c N) (а – b) c = ac – bc; Задача 8. Доказать свойства: а) коммутативность операции умножения; б) дистрибутивность операции умножения относительно сложения. Решение.а) Докажем, что ( а, b N0) а b = b а Дадим теоретико-множественное истолкование числовых выражений, записанных в левой и правой частях этого числового равенства. Пусть а = п(А); b= п(В), тогда аb = п (АВ),а b = п (ВА).Хотя декартово умножение не коммутативно (вообще говоря, АВ ВА), справедливо равенство п(АВ) = п (В А). Чтобы доказать это, поставим в соответствие каждой паре (х, у) из АВ пару (у, х) из В А, и наоборот, тогда между множествами A В и В А будет установлено взаимно однозначное соответствие и множества АВ и ВА будут равночисленны. Символически это записать так: 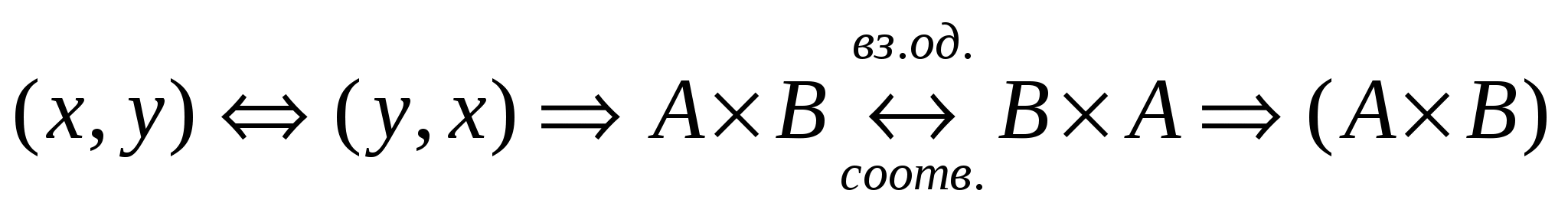 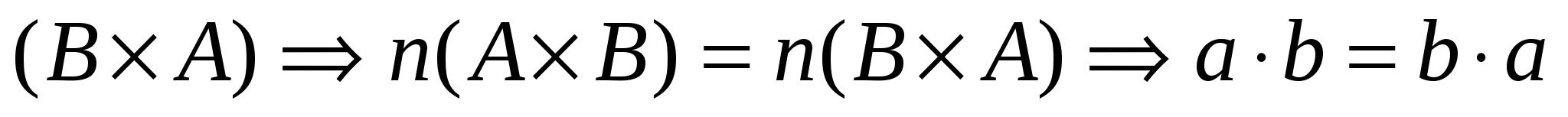 б) Докажем, что ( а, b,c N) а ( b + c) ab +ac; Дадим теоретико-множественное истолкование числовых выражений, записанных в левой и правой частях этого числового равенства. Пусть а = п(А); b= п(В); с = п(С), тогда b + с = п(В С), если В С=, а(b + с) = п(А (В С)), аb = п (А В); ас = п(АС), аb + ас = п((А В) (А С)), если (А В) (АС) =.Имеет место свойство дистрибутивности декартова умножения относительно объединения множеств, т.е. А (B С) = (АB) (АC).Если множества равны, то и количество элементов их одинаково, т.е. п(А(ВС)) = п((А В)(А С)). Символически это можно записать так: А (В С) = (А В) (А С) => п (А (В C) = п((А В) (А С)) => а(b + с) = аb + ас.В школе используется определение умножения, основанное на понятии суммы одинаковых слагаемых. ______________________________________________________________________ Определение 12. Если а и b – целые неотрицательные числа, то:  ab = а + а+…+а ab = а + а+…+а при b>1; bслагаемыха 1 = а bслагаемыха 1 = а при b=1а 0 = 0 при b = 0.______________________________________________________________________ Первую строчку определения можно сформулировать так: произведением чисел а и bназовем сумму bслагаемых, каждое из которых равно а. Из данного определения следует, что если множества A1, А2,...,Аbимеют по а элементов каждое, причем никакие два из них не пересекаются, то их объединение А1А2 ... Аbсодержит а bэлементов. Таким образом, произведение а b равно числу элементов в объединении bмножеств, каждое из которых содержит по а элементов, и никакие два из них не пересекаются. Символически это можно записать так: А1 А2 ... Аb = А, причем АiAj = , где i j и i, j =1,2, ...,bп(А1) = п(А2) =... = п(Аb)=a, тогда п(А) = п(А1 А2... Аb) = п(А1) + п(А2) + ... + п(Аb)= а + а+ +... + а = аb. В начальном курсе математики определение произведения вводится по частям: сначала появляется определение «Сумму одинаковых слагаемых называют произведением», например, 2 + 2 + 2 + 2 = 2 4, затем «При умножении любого числа на единицу получается то число, которое умножали», и запись а 1 = а и, наконец, «Произведение любого числа и нуля считают равным нулю» и запись а 0 = 0.
|
|
|
 Скачать 7.87 Mb.
Скачать 7.87 Mb. –
– 





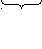
 ab = а + а+…+а при b>1;
ab = а + а+…+а при b>1; bслагаемых
bслагаемых