Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы

• Название: Контрольные вопросы для самоконтроля по усвоению теоретического материала, здесь же предлагается комплекс упражнений для самостоятельной работы
• Анкор: Praktikum_po_mat.doc
• Дата: 02.05.2017
• Размер: 7.87 Mb.
• Имя файла: Praktikum_po_mat.doc
• Тип: Контрольные вопросы; #6276
• страница: 11 из 19

3. БИНАРНЫЕ ОТНОШЕНИЯ

Пусть р  ХY; если Х = Y, то в этом случае говорят о бинарном отношении между элементами одного множества или об отношении на множестве и пишут p  х или р  х²

Отношения на множестве Xмогут обладать следующими свойствами:

1. 
   Говорят, что отношение р обладает свойством рефлексивности, если для любого х из множества Х истинно х р х, другими словами, если каждый элемент х Х находится в отношении р с самим собой (хХ)х р х – И.
   
2. 
   Говорят, что отношение р обладает свойством антирефлексивности если о любом элементе множества х можно сказать, что он не находится в отношении р с самим собой.
   

(х Х)–И.

3. 
   Говорят, что отношение р обладает свойством симметричности, если для всех элементов х и у из множества Х истинно утвержде­ние: если элемент х находится в отношении р с элементом у, то и элемент у находится в отношении р с элементом х.
   

(х, у Х)хру  урх –И.

4. 
   Говорят, что отношение/» обладает свойством антисимметрич­ности, если для всех различных элементов х и у из множества Xиз того, что элемент х находится в отношении р с элементом у, сле­дует, что элемент у не находится в отношении р с элементом х.
   

(х, у Х, х  у)х р у – И.

5. 
   Говорят, что отношение р обладает свойством транзитивности, если для всех элементов х, у, zиз множества Xистинно утверждение: если элемент х находится в отношении p с элементом у и элемент у находится в отношении р с элементом z, то элемент х находится в отношении р с элементом z.
   

(х, у,z Х)х р у  у р z х р z – И.

6. 
   Говорят, что отношение р обладает свойством связности, если для любых элементов х и у из множествах Х и х  у, следует, что или х находится в отношении р с у, или у находится в отношении р с х.
   

(х, уХ, х  у)х р у или у р х – И.

Указанные свойства отношений позволяют выделить два вида отношений.

1. Отношение р на множестве Xназывается отношением эквивалентности, если оно обладает свойствами рефлективности, симметричности и транзитивности.

Имеет место теорема:

Для того чтобы отношение р определяло разбиение множества Х на классы, необходимо и достаточно, чтобы р было отношением эквивалентности.

2. Отношение р на множестве Xназывается отношением порядка, если оно обладает свойствами антисимметричности и транзитивности.

Множество Х сзаданным на нем отношением порядка называется упорядоченным множеством.

Если отношение порядка, заданное на множестве X, обладает свойством связности, то говорят, что оно линейно упорядочивает множество X.
Задача 6.

На множестве Х = {1, 2, 3, 4, 5} задано отношение p, хру х >y

а) задать отношение перечислением пар;

б) построить граф отношения;

в) определить вид отношения.

Решение.

а) а = {(2,1); (3,1); (3,2); (4,1); (4,2); (4,3);(5,1); (5,2); (5,3); (5,4)}

б
2

1. 
   3
   

5 4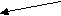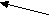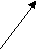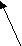
)



в) Определим, какими свойствами обладает отношение.

1. 
   Сформулируем свойство рефлективности: (хХ)х > х – Л. Получим ложное высказывание, отношение свойством рефлективности не обладает.
   

Следовательно, Р не является отношением эквивалентности.

2. 
   Проверим далее остальные свойства.
   
3. 
   Антирефлексивность:(xX) –- истинно, обладает.
   
4. 
   Симметричность: (х, у  Х)х > у  у > х – ложно, не обладает.
   
5. 
   Антисимметричность: (х, уХ, х  у) х > у  – истинно, обладает.
   
6. 
   Транзитивность: (х, у, zХ), х > у и у > zx > z – истинно, обладает.
   
7. 
   Связность: (х, уХ, х  у) х > у или у > х – истинно, обладает.
   

Отношение р обладает свойствами антисимметричности и транзитивности, значит, оно отношение порядка, а т.к. оно обладает еще свойствами антирефлексивности и связности, то оно – отношение строгого линейного порядка, и множество Xэтим отношением линейно упорядочено (5 > 4 > 3 > 2 >1).
Задача 7.

На множестве Х= {х/х N, х < 12} задано отношение К – «иметь один и тот же остаток при делении на 4». Объясните, почему отношение К является отношением эквивалентности, и запишите классы разбиения множества, определяемые этим отношением.

Решение. Отношение К является отношением эквивалентности, т.к. оно рефлексивно (можно сказать, что любое число имеет один и тот же остаток при делении на 4 с самим собой), симметрично (если число х имеет один и тот же остаток при делении на 4 с числом у, то и число у имеет один и тот же остаток при делении на 4 с числом х), транзитивно (если число х имеет при делении на 4 тот же остаток, что и число у, а число у имеет при делении на 4 тот же остаток, что и число z, то числа х иzимеют равные остатки при делении на 4).

Как известно, любое отношение эквивалентности, заданное на множестве X, определяет разбиение этого множества на классы таким образом, что в один класс попадают элементы, находящиеся в данном отношении, а в разные классы – не находящиеся в нем. Таким образом, каждый класс будет состоять из чисел, дающих один и тот же остаток при делении на 4. Таких классов 4: {1, 5, 9}, {2, 6, 10}, {3, 7, 11}, {4, 8, 12}.

АЛГЕБРАИЧЕСКИЕ ОПЕРАЦИИ

Определение 10. Алгебраической операцией на множестве Х называется соответствие, при котором каждой паре элементов из множества Х соответствует единственный элемент этого же множества.

Условились алгебраические операции обозначить символами ( читается «звездочка») и (читается «кружок»).

Определение алгебраической операции символически можно записать так: - алгебраическая опреация на множестве Х, если ( х, у  Х) ( ! z Х) х у= z.

Определение 11. Частичной алгебраической операцией на множестве называется соответствие, при котором некоторым парам элементов из множества Х соответствует единственный элемент того же множества.


Свойства алгебраических операций

1. 
   Алгебраическая операция, заданная на множестве Х, называется ассоциативной (обладает свойством ассоциативности), если для любых элементов х, у, z из множества Х выполняется равенство (х у)z = х (у z).
   
2. 
   Алгебраическая операция на множестве Х называется коммутативной (обладает свойством коммутативности), если для любых двух элементов х и у из множества выполняется равенство х у = у х.
   
3. 
   Алгебраическая операция называется дистрибутивной (обладает свойством дистрибутивности) относительно алгебраической операции , если для любых элементов у, х, и z из множества X выполняются равенства:
   

1) (х у) z = (х у) (у z) и 2) х (у z) = (х у) (х z)

4. Алгебраическая операция, заданная на множестве Х, называется сократимой (обладает свойством сократимости), если из условий а х = а у и х а = у а следует, что х = у для любых элементов а, х, у.
Задача 8.

На множестве натуральных чисел, кратных 5, заданы операции: сложение, вычитание. Какие из них являются на этом множестве:

а) алгебраическими;

б) частично алгебраическими ?

Решение. Пусть Х – множество натуральных чисел, кратных 5.

Любое натуральное число, кратное 5, имеет вид 5п, где пN.

Пусть 5n и 5m – два натуральных числа из множества Х, n  N, mN.

Тогда 5n + 5m= 5(n + m), причем (n + m) – сумма двух натуральных чисел, и, значит, число натуральное и единственное. Следовательно, складывая два любых натуральных числа, кратных 5, мы всегда получаем число, кратное 5, и это число единственное. Таким образом сложение на данном множестве Х есть алгебраическая операция.

Рассмотрим вычитание на множестве Х : 5n – 5m = 5(n – m), но n – mсуществует на множестве натуральных чисел лишь при условии, чтоnm, то разность 5n – 5mсуществует и является числом, кратным 5. Таким образом, вычитание на множестве Х есть частичная алгебраическая операция.

Контрольные вопросы

1. 
   Что называется отношением на множестве А?Приведите примеры отношения на множестве А = {1, 2, 3, 4, 5, 6}.
   
2. 
   Сформулируйте свойства отношения эквивалентности, приведите примеры.
   
3. 
   Сформулируйте свойства отношения порядка, отношения строгого линейного порядка, приведите примеры.
   
4. 
   Какова связь отношения эквивалентности, заданного на множестве, и разбиения множества на классы? Приведите примеры.
   
5. 
   Сформулировать определение алгебраической операции на множестве Х.
   
6. 
   Приведите примеры алгебраических операций на множестве целых чисел.
   
7. 
   Приведите примеры операций, не являющихся алгебраическими на множестве целых чисел.
   

Упражнения

261. На множестве B = {¹/₂, ³/₄, ⁵/₁₀, ²⁵/₅₀, ⁶/₈ , ⁴/₇} задано отношение «дробь х равна дроби у». Объясните, почему данное отношение является отношением эквивалентности, и запишите классы раз­биения множества В, определяемые им. Задайте на множестве В какое-нибудь отношение порядка.

262. Элементами множествах являются уравнения:

{2x – 3 = 1, 4х + 1 = – 1, х + 4 = 6, 6х + 5 = 2, – 6х + 9 = – 3, (2х + 1) = 0}.

Объясните, почему отношение «уравнение х равносильно уравнению у»является отношением эквивалентности, и запишите классы разбиения множества X, определяемые данным отношением.

263. Дано множество В = {23, 32, 24 – 18, 2³, 24, 12 – 3}. Какое из следующих отношений определяет разбиение множества на классы:

К – «значение выражения х меньше значения выражения у»;

Р – «значение выражения х равно значению выражения у»? выпишите эти классы?

264. На отрезке целых неотрицательных чисел от 0 до 999 задано отношение «иметь в записи одно и то же число цифр». Покажите, что оно является отношением эквивалентности; назовите наименьший и наибольший элементы каждого класса разбиения данного множества.

265. Сколько классов эквивалентности определяет на множестве целых неотрицательных чисел отношение «оканчивается одной и той же цифрой»? Назовите по одному представителю каждого класса. Задайте на множестве целых неотрицательных чисел какое-либо отношение порядка.

266. Какими свойствами обладают отношения равенства и включения для множеств? Есть ли среди них отношение порядка?

267. Отношение К – «иметь один и тот же остаток при делении на 3» – задано на множестве X = {х/хN, х < 10}. Объясните, почему отношение К является отношением эквивалентности, и запишет классы эквивалентности, определяемые этим отношением.

268. На множестве А = {5, 6, 7, 8, 9, 10} задано отношение р, х р у  х<у. Покажите, что оно является отношением порядка. Являете ли оно отношением линейного порядка?

269. На множестве А = {1, 2, 3, 4, 5,6,7} задано отношение К, х К у (х + у)2. Объясните, почему данное отношение является отношением эквивалентности, и запишите классы разбиения множества А, определяемые им.

270. На множестве А = {2, 3, 4, 5, 6, 7, 8, 9} задано отношение R, х R у х у. Покажите, что оно является отношением порядка. Является оно отношением линейного порядка?

271. Определите свойства следующих отношений:

Отношение «человек х одинакового роста с человеком у», заданного на множестве людей.

Отношение Е — «число х является модулем числа у» задано между элементами множеств А = {3, 4, 5, 6} и В = = {–3, –4, 3, 4, 5, –5, –6, 6}. Постройте граф и график отношения Е.

272. Элементы множества окружностей связаны отношением «окружность х касается окружности у».

273. На множестве людей задано отношение «человек х ниже человека у».

274. На множестве людей задано отношение «человек х имеет одинаковый цвет глаз с человеком у».

275. На множестве прямых задано отношение «прямая х перпендикулярна прямой у».

276. На множестве натуральных чисел задано отношение Р — «быть делителем». Какие из пар (2;15), (3; 12), (10; 150), (17; 17), (6; 15), (24; 6), (9; 1) принадлежат отношению Р?

277. Постройте график отношения, заданного на множестве действительных чисел уравнением: а) 3х + 4у = 12; б) у = 4 – х²; в) (х + 5)² + (у – 2)² = 4; г) у = –х² + 2х – 1; д) ху = 20.

278. Постройте график отношения, заданного на множестве действительных чисел при помощи неравенства:

а) 3х – 5у  4;

б) (х – 4)² + (у – 1)² > 36;

в) (х – 2)² + у²  4.

279. Сформулируйте свойства отношений «равно», «меньше», «не больше», «меньше на 2», заданных на множестве {1, 3, 5, 7, 9}, и постройте их графы. Какое из этих отношений является отношением: а) эквивалентности; б) порядка?

280. Докажите, что отношение «иметь один и тот же остаток при делении на 6», заданное на множестве натуральных чисел, является отношением эквивалентности. Сколько классов эквивалентности определяет это отношение?

281. Какие из следующих отношений являются отношениями эквивалентности, а какие — порядка: а) равенство на множестве геометрических фигур; б) подобие на множестве геометрических фигур; в) равносильности на множестве уравнений; г) перпендикулярность на множестве прямых; д) «быть длиннее» на множестве отрезков?

282. Доказать, что вычитание является алгебраической операцией на множестве Z, а деление не является алгебраической операцией.

283. Приведите примеры операций, которые являются алгебраическими на множестве:

а) высказываний ; б) всех подмножеств универсального множества И .

284. Доказать, что вычитание является алгебраической операцией на множестве целых чисел, а деление не является на этом же множестве.